山东省青岛市2022-2023学年九年级上学期期中数学试题
试卷更新日期:2022-12-20 类型:期中考试
一、单选题
-
1. 如图所示几何体的俯视图是( )
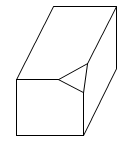 A、
A、 B、
B、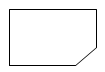 C、
C、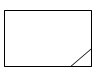 D、
D、 2. 在下列命题中,正确的是 ( )A、一组对边平行的四边形是平行四边形 B、有一个角是直角的四边形是矩形 C、有一组邻边相等的平行四边形是菱形 D、对角线互相垂直平分的四边形是正方形3. 某校生物兴趣小组为了解种子发芽情况,重复做了大量种子发芽的实验,结果如下:
2. 在下列命题中,正确的是 ( )A、一组对边平行的四边形是平行四边形 B、有一个角是直角的四边形是矩形 C、有一组邻边相等的平行四边形是菱形 D、对角线互相垂直平分的四边形是正方形3. 某校生物兴趣小组为了解种子发芽情况,重复做了大量种子发芽的实验,结果如下:实验种子的数量n
100
200
500
1000
5000
10000
发芽种子的数量m
98
182
485
900
4750
9500
种子发芽的频率
0.98
0.91
0.97
0.90
0.95
0.95
根据以上数据,估计该种子发芽的概率是( )
A、0.90 B、0.98 C、0.95 D、0.914. 如图,在平面点角坐标系中AOB与COD是位似图形,以原点O为位似中心,若 , B点坐标为(4,2),则点D的坐标为( )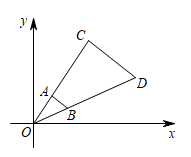 A、( 8,4) B、(8,6) C、(12,4) D、(12,6)5. 如图,在△ABC中,点D在BC边上,连接AD,点G在线段AD上,GE∥BD,且交AB于点E,GF∥AC,且交CD于点F,则下列结论一定正确的是( )
A、( 8,4) B、(8,6) C、(12,4) D、(12,6)5. 如图,在△ABC中,点D在BC边上,连接AD,点G在线段AD上,GE∥BD,且交AB于点E,GF∥AC,且交CD于点F,则下列结论一定正确的是( ) A、 B、 C、 D、6. 若关于x的方程有一个根为则另一个根为A、 B、2 C、4 D、7. 在同一直角坐标系中,函数与的图像大致是( )A、
A、 B、 C、 D、6. 若关于x的方程有一个根为则另一个根为A、 B、2 C、4 D、7. 在同一直角坐标系中,函数与的图像大致是( )A、 B、
B、 C、
C、 D、
D、 8. ABCD是边长为1的正方形,是等边三角形,则的面积为
8. ABCD是边长为1的正方形,是等边三角形,则的面积为 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
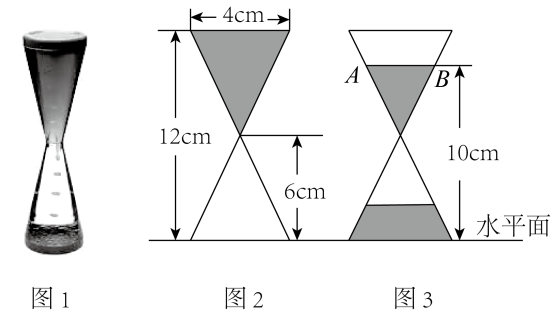
9. 一个不透明的布袋中,装有红、黄、白三种只有颜色不同的小球,其中红色小球有8个,黄、白色小球的数目相等,为估计袋中黄色小球的数目,每次将袋中小球搅匀后摸出一个小球记下颜色,再次搅匀多次试验发现摸到红球的频率是 , 则估计黄色小球的数目是个。10. 如果关于x的一元二次方程有实数根,那么k的取值范围是 .11. 如图1是液体沙漏的立体图形,图2,图3分别是液体沙漏某一时刻沙漏上半部分液体长度与液面距离水平面高度的平面示意图,则图3中AB=cm.
 12. 某机械厂七月份生产零件50万个,第三季度生产零件196万个.设该厂八、九月份平均每月的增长率为x,那么方程是 .13. 如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(―1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,……,依此规律跳动下去,点P第100次跳动至点P100的坐标是 .
12. 某机械厂七月份生产零件50万个,第三季度生产零件196万个.设该厂八、九月份平均每月的增长率为x,那么方程是 .13. 如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(―1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,……,依此规律跳动下去,点P第100次跳动至点P100的坐标是 . 14. 如图,正方形ABCD中,点O为AC中点,线段EF经过点O,∠FOC=60°,点G在线段OC上, , 连接EG.以下结论:①;②∠AEF=75°;③;④若 , 则的面积为3.其中正确的是 . (填写所有正确结论的序号)
14. 如图,正方形ABCD中,点O为AC中点,线段EF经过点O,∠FOC=60°,点G在线段OC上, , 连接EG.以下结论:①;②∠AEF=75°;③;④若 , 则的面积为3.其中正确的是 . (填写所有正确结论的序号)
三、解答题
-
15. 如图所示,一块儿三角形空地ABC,要在其内部建一个菱形花园,使得B为菱形花园的一个顶点,其余3个顶点分别在的3条边上.请你能设计出此菱形花园.
 16. 用指定的方法解下列方程.(1)、用配方法解方程;(2)、用公式法解方程 .17. 关于x的一元二次方程(k-2)x2-4x+2=0有两个不相等的实数根.(1)、求k的取值范围;(2)、如果k是符合条件的最大整数,且一元二次方程x2-4x+k=0与x2+mx-1=0有一个相同的根,求此时m的值.18. 某校举办以2022年北京冬奥会为主题的知识竞赛,从七年级和八年级各随机抽取了50名学生的竞赛成绩进行整理、描述和分析,部分信息如下:
16. 用指定的方法解下列方程.(1)、用配方法解方程;(2)、用公式法解方程 .17. 关于x的一元二次方程(k-2)x2-4x+2=0有两个不相等的实数根.(1)、求k的取值范围;(2)、如果k是符合条件的最大整数,且一元二次方程x2-4x+k=0与x2+mx-1=0有一个相同的根,求此时m的值.18. 某校举办以2022年北京冬奥会为主题的知识竞赛,从七年级和八年级各随机抽取了50名学生的竞赛成绩进行整理、描述和分析,部分信息如下:a:七年级抽取成绩的频数分布直方图如图.(数据分成5组, , , , , )
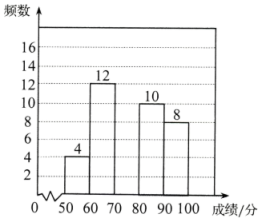
b:七年级抽取成绩在7这一组的是:70,72,73,73,75,75,75,76,77,77,78,78,79,79,79,79.
c:七、八年级抽取成绩的平均数、中位数如下:
年级
平均数
中位数
七年级
76.5
m
八年级
78.2
79
请结合以上信息完成下列问题:
(1)、七年级抽取成绩在的人数是 , 并补全频数分布直方图;(2)、表中m的值为;(3)、七年级学生甲和八年级学生乙的竞赛成绩都是78,则(填“甲”或“乙”)的成绩在本年级抽取成绩中排名更靠前;(4)、七年级的学生共有400人,请你估计七年级竞赛成绩90分及以上的学生人数.19. 某天晚上,小明看到人民广场的人行横道两侧都有路灯,想起老师数学课上学习身高与影长的相关知识,于是自己也想实际探究一下.为了探究自己在两路灯下的影长和在两路灯之间的位置关系,小明在网上从有关部门查得左侧路灯(AB)的高度为4.8米,右侧路灯(CD)的高度为6.4米,两路灯之间的距离(BD)为12米,已知小明的身高(EF)为1.6米,然后小明在两路灯之间的线段上行走(如图所示),测量相关数据. (1)、若小明站在人行横道的中央(点F是BD的中点)时,小明测得自己在两路灯下的影长FP=米,FQ=米;(2)、小明在移动过程中,发现在某一点时,两路灯产生的影长相等(FP=FQ),请问时小明站在什么位置,为什么?20. 已知:如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.
(1)、若小明站在人行横道的中央(点F是BD的中点)时,小明测得自己在两路灯下的影长FP=米,FQ=米;(2)、小明在移动过程中,发现在某一点时,两路灯产生的影长相等(FP=FQ),请问时小明站在什么位置,为什么?20. 已知:如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G. (1)、求证:△ADE≌△CBF;(2)、若四边形BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.21. 某种商品上市之初采用了大量的广告宣传,其销售量与上市的天数之间成正比,当广告停止后,销售量与上市的天数之间成反比(如图),现已知上市30天时,当日销售量为120万件.
(1)、求证:△ADE≌△CBF;(2)、若四边形BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.21. 某种商品上市之初采用了大量的广告宣传,其销售量与上市的天数之间成正比,当广告停止后,销售量与上市的天数之间成反比(如图),现已知上市30天时,当日销售量为120万件. (1)、写出该商品上市以后销售量y(万件)与时间x(天数)之间的表达式;(2)、求上市至第100天(含第100天),日销售量在36万件以下(不含36万件)的天数;(3)、广告合同约定,当销售量不低于100万件,并且持续天数不少于12天时,广告设计师就可以拿到“特殊贡献奖”,那么本次广告策划,设计师能否拿到“特殊贡献奖”?22. 2022年2月4日,第24届冬季奥林匹克运动会将在北京举行,吉祥物“冰墩墩”备受人民的喜爱. 某商店经销一种吉祥物玩具,销售成本为买件40元,据市场分析,若按每件50元销售,一个月能售出500件;销售单价每涨2元,月销售量就减少20件,针对这种玩具的销售情况,请解答以下问题:(1)、当销售单价涨多少元时,月销售利润能够达到8000元.(2)、商店想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,则销售定价应为多少元?23. [问题提出]如图1,由(长×宽×高)个小立方块组成的正方体中,到底有多少个长方体(包括正方体)呢?
(1)、写出该商品上市以后销售量y(万件)与时间x(天数)之间的表达式;(2)、求上市至第100天(含第100天),日销售量在36万件以下(不含36万件)的天数;(3)、广告合同约定,当销售量不低于100万件,并且持续天数不少于12天时,广告设计师就可以拿到“特殊贡献奖”,那么本次广告策划,设计师能否拿到“特殊贡献奖”?22. 2022年2月4日,第24届冬季奥林匹克运动会将在北京举行,吉祥物“冰墩墩”备受人民的喜爱. 某商店经销一种吉祥物玩具,销售成本为买件40元,据市场分析,若按每件50元销售,一个月能售出500件;销售单价每涨2元,月销售量就减少20件,针对这种玩具的销售情况,请解答以下问题:(1)、当销售单价涨多少元时,月销售利润能够达到8000元.(2)、商店想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,则销售定价应为多少元?23. [问题提出]如图1,由(长×宽×高)个小立方块组成的正方体中,到底有多少个长方体(包括正方体)呢?
[问题探究]我们先从较为简单的情形入手.
如图2,由个小立方块组成的长方体中,长共有条线段,宽和高分别只有1条线段,所以图中共有个长方体.
如图3,由个小立方块组成的长方体中,长和宽分别有条线段,高有1条线段,所以图中共有个长方体.
(1)、如图4,由个小立方体组成的正方体中,长、宽、高分别有条线段,所以图中共有个长方体.(2)、由个小立方块组成的长方体中,长共有条线段,宽共有条线段,高共有条线段,所以图中共有个长方体.(3)、[问题解决]由个小立方块组成的正方体中,长、宽、高各有条线段,所以图中共有个长方体.(4)、[结论应用]如果由若干个小立方块组成的正方体中共有1000个长方体,那么组成这个正方体的小立方块的个数是多少?请通过计算说明你的结论.24. 已知:线段和矩形如图①摆放(点与点重合),点在边上, . 如图②,从图①的位置出发,沿方向运动,速度为;动点同时从点出发,沿方向运动,速度为 . 点为的中点,连接与相交于点 , 设运动时间为 . 解答下列问题: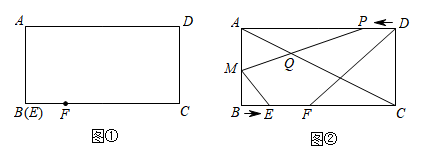 (1)、当时,求的值;(2)、设五边形的面积为 , 求与的关系式;(3)、当时,求线段的长;(4)、当为何值时,五边形的周长最小,最小是多少?(直接写出答案即可)
(1)、当时,求的值;(2)、设五边形的面积为 , 求与的关系式;(3)、当时,求线段的长;(4)、当为何值时,五边形的周长最小,最小是多少?(直接写出答案即可)