山东省临沂市莒南县2022-2023学年九年级上学期期中数学试题
试卷更新日期:2022-12-20 类型:期中考试
一、单选题
-
1. 下列图形中,是中心对称图形的是( ).A、
 B、
B、 C、
C、 D、
D、 2. 下列关于抛物线的性质说法正确的是( )A、开口向上 B、顶点坐标是(2,3) C、对称轴是直线x=-2 D、当-5<x≤0时,-6<y≤-13. 如图,点A在反比例函数第一象限内的图象上,点B在x轴的正半轴上,OA=AB,△AOB的面积为2,则a的值为( )
2. 下列关于抛物线的性质说法正确的是( )A、开口向上 B、顶点坐标是(2,3) C、对称轴是直线x=-2 D、当-5<x≤0时,-6<y≤-13. 如图,点A在反比例函数第一象限内的图象上,点B在x轴的正半轴上,OA=AB,△AOB的面积为2,则a的值为( )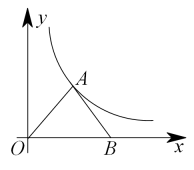 A、 B、 C、2 D、14. 关于函数的图像,下列说法错误的是( )A、该函数图象是双曲线 B、经过点 C、在第二象限内,y随x的增大而增大 D、是中心对称图,且对称中心是坐标原点5. 点A(-2,),B(0,),C(1,)为二次函数的图象上的三点,则y1 , y2 , y3的大小关系是( )A、 B、 C、 D、6. 如图,PA,PB切⊙O 于点A,B,PA=20,CD切⊙O于点E,交PA,PB于C,D两点,则△PCD 的周长是( )
A、 B、 C、2 D、14. 关于函数的图像,下列说法错误的是( )A、该函数图象是双曲线 B、经过点 C、在第二象限内,y随x的增大而增大 D、是中心对称图,且对称中心是坐标原点5. 点A(-2,),B(0,),C(1,)为二次函数的图象上的三点,则y1 , y2 , y3的大小关系是( )A、 B、 C、 D、6. 如图,PA,PB切⊙O 于点A,B,PA=20,CD切⊙O于点E,交PA,PB于C,D两点,则△PCD 的周长是( ) A、20 B、36 C、40 D、447. 如图,在△ABC中, , , 点D,E分别在AC和BC上, , 若以DE为直径的⊙O交AB的中点F,则⊙O的直径是( )
A、20 B、36 C、40 D、447. 如图,在△ABC中, , , 点D,E分别在AC和BC上, , 若以DE为直径的⊙O交AB的中点F,则⊙O的直径是( ) A、 B、2 C、 D、58. 已知二次函数的图像如图所示,则一次函数与反比例函数的图像可能是( )
A、 B、2 C、 D、58. 已知二次函数的图像如图所示,则一次函数与反比例函数的图像可能是( ) A、
A、 B、
B、 C、
C、 D、
D、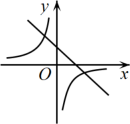 9. 如图,在正方形ABCD中,AB=4,点M在CD的边上,且DM=1,△AEM与△ADM关于AM所在的直线对称,将△ADM按顺时针方向绕点A旋转90°得到△ABF,连接EF,则线段EF的长为( )
9. 如图,在正方形ABCD中,AB=4,点M在CD的边上,且DM=1,△AEM与△ADM关于AM所在的直线对称,将△ADM按顺时针方向绕点A旋转90°得到△ABF,连接EF,则线段EF的长为( ) A、3 B、2 C、5 D、10. 如图正方形和正方形全等,把点A固定在正方形的中心,当正方形绕点A转动时,两个正方形重叠部分的面积是正方形面积的( )
A、3 B、2 C、5 D、10. 如图正方形和正方形全等,把点A固定在正方形的中心,当正方形绕点A转动时,两个正方形重叠部分的面积是正方形面积的( ) A、 B、 C、 D、11. 如图, 中, 于点 是半径为2的上一动点, 连结 , 若是的中点, 连结 , 则长的最大值为 ( )
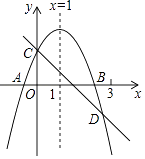
A、 B、 C、 D、11. 如图, 中, 于点 是半径为2的上一动点, 连结 , 若是的中点, 连结 , 则长的最大值为 ( ) A、3 B、 C、4 D、12. 如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,则下列结论:
A、3 B、 C、4 D、12. 如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,则下列结论:①2a+b+c>0;②a﹣b+c<0;③x(ax+b)≤a+b;④a<﹣1.
其中正确的有( )
 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
13. 下列说法中正确的有(填序号).
(1)直径是圆中最大的弦;(2)长度相等的两条弧一定是等弧;(3)半径相等的两个圆是等圆;(4)面积相等的两个圆是等圆;(5)同一条弦所对的两条弧一定是等弧.14. 反比例函数 , 当时,函数值的取值范围 .15. 如图,P是正方形ABCD内一点,且点P到点B、C、D的距离分别为、、4,则的度数为 16. 如图,平行于x轴的直线分别交抛物线与于B,C两点,过点C作y轴的平行线交于点D,直线交于点E,则的值是 .
16. 如图,平行于x轴的直线分别交抛物线与于B,C两点,过点C作y轴的平行线交于点D,直线交于点E,则的值是 .
三、解答题
-
17. 如图,已知△ABC在平面直角坐标系中的位置如图所示.
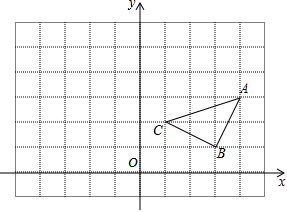 (1)、写出△ABC三个顶点的坐标;(2)、画出△ABC关于点C的中心对称图形;(3)、求出△ABC的面积.18. 如图,在ABC中,∠B=90°,AB=6cm,AC=10cm,点P从点A开始沿AB向点B以1cm/s的速度移动,点Q从B点开始沿BC向点C以2cm/s的速度移动,P、Q两点同时出发,当一个点到达终点时另一个点也随之停止运动,运动时间为t.
(1)、写出△ABC三个顶点的坐标;(2)、画出△ABC关于点C的中心对称图形;(3)、求出△ABC的面积.18. 如图,在ABC中,∠B=90°,AB=6cm,AC=10cm,点P从点A开始沿AB向点B以1cm/s的速度移动,点Q从B点开始沿BC向点C以2cm/s的速度移动,P、Q两点同时出发,当一个点到达终点时另一个点也随之停止运动,运动时间为t.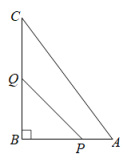 (1)、几秒后四边形APQC的面积是19平方厘米;(2)、若用S表示四边形APQC的面积,经过多长时间S取得最小值,并求出S的最小值.19. 某服装批发市场销售一种衬衫,衬衫每件进货价为50元,规定每件售价不低于进货价,经市场调查,每月的销售量y(件)与每件的售价x(元)满足一次函数关系 .(1)、该批发市场每月想从这种衬衫销售中获利24000元,又想尽量给客户实惠,该如何给这种衬衫定价?(2)、物价部门规定,该衬衫的每件利润不允许高于进货价的30%,设这种衬衫每月的总利润为w(元),那么售价定为多少元可获得最大利润?最大利润是多少?20. 如图,是直径,弦于点E,过点C作的垂线,交的延长线于点G,垂足为点F,连结 , 其中 .
(1)、几秒后四边形APQC的面积是19平方厘米;(2)、若用S表示四边形APQC的面积,经过多长时间S取得最小值,并求出S的最小值.19. 某服装批发市场销售一种衬衫,衬衫每件进货价为50元,规定每件售价不低于进货价,经市场调查,每月的销售量y(件)与每件的售价x(元)满足一次函数关系 .(1)、该批发市场每月想从这种衬衫销售中获利24000元,又想尽量给客户实惠,该如何给这种衬衫定价?(2)、物价部门规定,该衬衫的每件利润不允许高于进货价的30%,设这种衬衫每月的总利润为w(元),那么售价定为多少元可获得最大利润?最大利润是多少?20. 如图,是直径,弦于点E,过点C作的垂线,交的延长线于点G,垂足为点F,连结 , 其中 . (1)、求证:;(2)、若 , 求的半径.21. 如图,在矩形ABCD中,AB=4cm,AD=3cm,动点P从点A出发,以1cm/s的速度沿射线AB运动.点Q在射线BA上(在点P的左侧),且PQ=6cm,以线段PQ为斜边向直线AB上方作等腰直角△PQM,设点P的运动时间为x(s),△PQM与矩形ABCD重叠部分图形的面积为y(cm).
(1)、求证:;(2)、若 , 求的半径.21. 如图,在矩形ABCD中,AB=4cm,AD=3cm,动点P从点A出发,以1cm/s的速度沿射线AB运动.点Q在射线BA上(在点P的左侧),且PQ=6cm,以线段PQ为斜边向直线AB上方作等腰直角△PQM,设点P的运动时间为x(s),△PQM与矩形ABCD重叠部分图形的面积为y(cm). (1)、当点P与点B重合时,直接写出DM的长;(2)、当△PQM与矩形ABCD重叠部分图形不是三角形,且y>0时,求y关于x的函数关系式,并写出自变量x的取值范围.22. 已知,AB是⊙O的直径,AB=16,点C在⊙O的半径OA上运动,PC⊥AB,垂足为C,PC=10,PT为⊙O的切线,切点为T.
(1)、当点P与点B重合时,直接写出DM的长;(2)、当△PQM与矩形ABCD重叠部分图形不是三角形,且y>0时,求y关于x的函数关系式,并写出自变量x的取值范围.22. 已知,AB是⊙O的直径,AB=16,点C在⊙O的半径OA上运动,PC⊥AB,垂足为C,PC=10,PT为⊙O的切线,切点为T.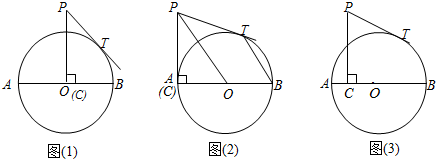 (1)、如图(1),当C点运动到O点时,求PT的长;(2)、如图(2),当C点运动到A点时,连接PO、BT,求证:PO∥BT;(3)、如图(3),设PT=y,AC=x,求y与x的解析式并求出y的最小值.23. 若任意两个正数的和为定值,则它们的乘积会如何变化呢?会不会存在最大值?
(1)、如图(1),当C点运动到O点时,求PT的长;(2)、如图(2),当C点运动到A点时,连接PO、BT,求证:PO∥BT;(3)、如图(3),设PT=y,AC=x,求y与x的解析式并求出y的最小值.23. 若任意两个正数的和为定值,则它们的乘积会如何变化呢?会不会存在最大值?特例研究:若两个正数的和是1,那么这两个正数可以是:和 , 和 , 和 , …
由于这样的正数有很多,我们不妨设其中一个正数是 , 另外一个正数为 , 那么 , 则 , 所以 , , 可以看出两数的乘积是的二次函数,乘积的最大值转化为求关于的二次函数的最值问题.
方法迁移:
(1)、若两个正数x和y的和是6,其中一个正数为 , 这两个正数的乘积为z,写出z与x的函数关系式,并画出函数图象. (2)、在(1)的条件下,z的最大值为: , 并写出此时函数图象的至少一个性质 .(3)、问题解决:
(2)、在(1)的条件下,z的最大值为: , 并写出此时函数图象的至少一个性质 .(3)、问题解决:由以上题目可知若任意两个正数的和是一个固定的数,那么这两个正数的乘积存在最大值,即对于正数x,y,若x+y是定值,则xy存在最大值.
类比应用:
利用上面所得到的结论,完成填空:
①已知函数与函数 , 则当x=时,取得最大值为;
②已知函数y1=2x-2+m(x≥1),m为正定值,函数y2=-2x+8(x<4),则当x为何值时,取得最大值,最大值是多少?