山东省济宁市2022-2023学年九年级上学期期中数学试题

试卷更新日期：2022-12-20 类型：期中考试

进入出卷网下载

一、单选题

1. 下列四个图形中，既是轴对称图形又是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 如图，点A、B、C是 $⊙ O$ 上的三点， $∠ B A C = 40 °$ ，则 $∠ B O C$ 的度数是（）

A、 $80 °$ B、 $40 °$ C、 $50 °$ D、 $20 °$

查看试题解析
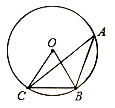3. 已知⊙O的半径等于5，圆心O到直线l的距离为6，那么直线l与⊙O的公共点的个数是（）

A、0 B、1 C、2 D、无法确定

查看试题解析
4. 一元二次方程 $x^{2} + 6 x - 3 = 0$ 配方后可变形为（）

A、 ${(x + 3)}^{2} = 9$ B、 ${(x - 3)}^{2} = 12$ C、 ${(x + 3)}^{2} = 12$ D、 ${(x - 3)}^{2} = 9$

查看试题解析
5. 在平面直角坐标系中，将抛物线y＝x²向上平移一个单位长度，再向右平移一个单位长度，得到的抛物线解析式是（）

A、y＝(x－1)²－1 B、y＝(x－1)²＋1 C、y＝(x＋1)²－1 D、y＝(x＋1)²＋1

查看试题解析
6. 已知m、n是一元二次方程 $x^{2} + 2 x - 5 = 0$ 的两个根，则 $m^{2} + m n + 3 m + n$ 的值为（）

A、 $- 1$ B、 $- 2$ C、 $- 3$ D、 $- 5$

查看试题解析
7. 抛掷一枚质地均匀的硬币三次，恰有两次正面向上的概率是（）

A、 $\frac{1}{8}$ B、 $\frac{1}{4}$ C、 $\frac{3}{8}$ D、 $\frac{5}{8}$

查看试题解析
8. 已知二次函数 $y = a x^{2} - 2 a x + 1$ （ $a$ 为常数，且 $a > 0$ ）的图象上有三点 $A (- 2 ， y_{1})$ ， $B (1 ， y_{2})$ ， $C (3 ， y_{3})$ ，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{1} < y_{3} < y_{2}$ C、 $y_{2} < y_{1} < y_{3}$ D、 $y_{2} < y_{3} < y_{1}$

查看试题解析
9. 能使分式方程 $\frac{k}{1 - x} + 2 = \frac{3}{x - 1}$ 有非负实数解，且使二次函数 $y = x^{2} + 2 x - k - 1$ 的图象与x轴无交点的所有整数k的积为（）

A、 $- 20$ B、20 C、 $- 60$ D、60

查看试题解析
10. 如图，二次函数 $y = a x^{2} + b x + c （ a \neq 0 ）$ 的图象与x轴交于点A（-2，0），与y轴的交点在（0，-2）和（0，-1）之间（不包括这两点），对称轴为直线 $x = 1$ .有下列结论：① $a b c > 0$ ；② $4 a + 2 b + c > 0$ ；③ $\frac{1}{8} < a < \frac{1}{4}$ ；④ $b < c$ .其中正确的（）

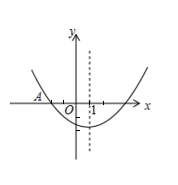A、①② B、①③ C、①④ D、③④

查看试题解析

二、填空题

11. 在平面直角坐标系中，点（3，-2）关于原点对称的点的坐标是．

查看试题解析
12. 已知圆锥的底面圆半径为4，母线长为5，则圆锥的侧面积是.

查看试题解析
13. 如图， $P M$ ， $P N$ 分别与 $⊙ O$ 相切于A， $B$ 两点， $C$ 为 $⊙ O$ 上异于A， $B$ 的一点，连接 $A C$ ， $B C$ ，若 $∠ P = 58 °$ ，则 $∠ A C B$ 的大小是

查看试题解析
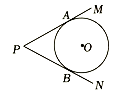14. 某品牌汽车刹车后行驶的距离s米与行驶的时间t秒的函数关系式是 $s = 30 t - 5 t^{2}$ ，汽车刹车后到停下来前进了米．

查看试题解析
15. 二次函数 $y = \frac{1}{2} x^{2} + \frac{1}{2} x$ 的图像如图所示，点 $A_{1} 、 A_{2} 、 A_{3} 、 A_{4} 、 ⋯ ⋯ 、 A_{2022}$ 在二次函数 $y = \frac{1}{2} x^{2} + \frac{1}{2} x$ 位于第一象限的图像上，点 $B_{1} 、 B_{2} 、 B_{3} 、 B_{4} 、 ⋯ ⋯ 、 B_{2022}$ 在y轴的正半轴上， $△ O A_{1} B_{1} 、 △ B_{1} A_{2} B_{2} 、 ⋯ ⋯ 、 △ B_{2021} A_{2022} B_{2022}$ 都是等腰直角三角形，则 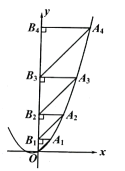$B_{2021} A_{2022} =$ ．

查看试题解析

三、解答题

16. 用适当的方法解下列方程.

(1)、 $x^{2} + 6 x = 1$ ；

(2)、 ${(x - 1)}^{2} = 5 (x - 1)$ .

查看试题解析
17. 如图，将△ABC绕点A逆时针旋转得到△ADE，点D在BC上，已知∠B＝70°，求∠CDE的大小．

查看试题解析
18. 如图，在平面直角坐标系中，△ABC的顶点坐标分别为A（ $- 1$ ， 0），B（ $- 4$ ， 1），C（ $- 2$ ， 2）．

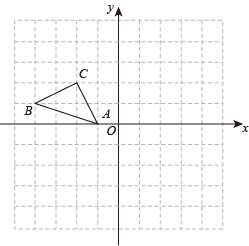
（1）直接写出点B关于点C对称的点 $B^{'}$ 的坐标：
（2）请画出△ABC关于点O成中心对称的 $△ A_{1} B_{1} C_{1}$ ；
（3）画出△ABC绕原点O逆时针旋转90°后得到的 $△ A_{2} B_{2} C_{2}$ ．

查看试题解析
19. 一个不透明的口袋中有三个完全相同的小球，把它们分别标号为1，2，3．甲从口袋中随机摸取一个小球，记下标号m，然后放回，再由乙从口袋中随机摸取一个小球，记下标号n，组成一个数对（m，n）．

(1)、用列表法或画树状图法，写出（m，n）所有可能出现的结果；

(2)、甲、乙两人玩游戏，规则如下：按上述要求，两人各摸取一个小球，小球上标号之和为奇数则甲赢，小球上标号之和为偶数则乙赢．你认为这个游戏规则公平吗？请说明理由．

查看试题解析
20. 如图， $A B$ 为 $⊙ O$ 的直径， $B C$ 是圆的切线，切点为B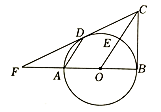， $O C$ 平行于弦 $A D$ .

(1)、求证： $D C$ 是 $⊙ O$ 的切线；

(2)、直线 $A B$ 与 $C D$ 交于点F，且 $D F = 4$ ， $A F = 2$ ，求 $⊙ O$ 的半径.

查看试题解析
21. 2022年北京冬奥会举办期间，冬奥会吉祥物“冰墩墩”深受广大人民的喜爱．某特许零售店“冰墩墩”的销售日益火爆．每个纪念品进价40元，规定销售单价不低于44元，且不高于52元．销售期间发现，当销售单价定为44元时，每天可售出300个，销售单价每上涨1元，每天销量减少10个．现商家决定提价销售，设每天销售量为y个，销售单价为x元．

(1)、直接写出y与x之间的函数关系式和自变量x的取值范围；

(2)、将纪念品的销售单价定为多少元时，商家每天销售纪念品获得的利润w元最大？最大利润是多少元？

(3)、该店主热心公益事业，决定从每天的利润中捐出200元给希望工程，为了保证捐款后每天剩余利润不低于2200元，求销售单价x的范围．

查看试题解析
22. 如图，已知二次函数y=ax²+bx+3的图象交x轴于点A（1，0），B（3，0），交y轴于点C．

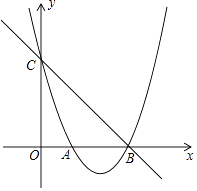(1)、求这个二次函数的表达式；

(2)、点P是直线BC下方抛物线上的一动点，求△BCP面积的最大值；

(3)、直线x=m分别交直线BC和抛物线于点M，N，当△BMN是等腰三角形时，直接写出m的值．

查看试题解析