山东省济南市章丘区2022-2023学年九年级上学期期中数学试题
试卷更新日期:2022-12-20 类型:期中考试
一、单选题
-
1. 下列判断中错误的是( )A、四个角相等的四边形是矩形 B、对角线互相垂直平分的四边形是正方形 C、对角线互相垂直的平行四边形是菱形 D、两组对边分别平行的四边形是平行四边形2. 不解方程,判断方程2x2-4x-1=0的根的情况是( )A、没有实数根 B、有两个相等实数根 C、有两个不相等实数根 D、无法确定3. 若 , 则( )A、 B、 C、 D、4. 某学校组织学生到社区开展公益宣传活动,成立了“垃圾分类”“文明出行”“低碳环保”三个宣传队,如果小华和小丽每人随机选择参加其中一个宣传队,则她们恰好选到同一个宣传队的概率是( )A、 B、 C、 D、5. 如图,DE∥BC,且EC:BD=2:3,AD=6,则AE的长为( )
 A、1 B、2 C、3 D、46. 某省加快新旧动能转换,促进企业创新发展.某企业一月份的营业额是1000万元,月平均增长率相同,第一季度的总营业额是3990万元.若设月平均增长率是x,那么可列出的方程是( )A、1000(1+x)2=3990 B、1000+1000(1+x)+1000(1+x)2=3990 C、1000(1+2x)=3990 D、1000+1000(1+x)+1000(1+2x)=39907. 如图,在菱形中,对角线 , 分别为16和12,于点E,则( )
A、1 B、2 C、3 D、46. 某省加快新旧动能转换,促进企业创新发展.某企业一月份的营业额是1000万元,月平均增长率相同,第一季度的总营业额是3990万元.若设月平均增长率是x,那么可列出的方程是( )A、1000(1+x)2=3990 B、1000+1000(1+x)+1000(1+x)2=3990 C、1000(1+2x)=3990 D、1000+1000(1+x)+1000(1+2x)=39907. 如图,在菱形中,对角线 , 分别为16和12,于点E,则( ) A、 B、 C、10 D、88. 下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )
A、 B、 C、10 D、88. 下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )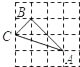 A、
A、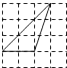 B、
B、 C、
C、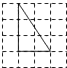 D、
D、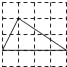 9. 如图,在矩形ABCD中,AB=24,BC=12,点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形.则AE的长是( )
9. 如图,在矩形ABCD中,AB=24,BC=12,点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形.则AE的长是( ) A、15 B、20 C、 D、10. 如图,在矩形纸片ABCD中, , , 将AB沿AE翻折,使点B落在处,AE为折痕,再将EC沿EF翻折,使点C恰好落在线段上的点处,EF为折痕,连接 . 若 , 则的值为( )
A、15 B、20 C、 D、10. 如图,在矩形纸片ABCD中, , , 将AB沿AE翻折,使点B落在处,AE为折痕,再将EC沿EF翻折,使点C恰好落在线段上的点处,EF为折痕,连接 . 若 , 则的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 关于 的一元二次方程 的一个根是2,则另一个根是 .12. 如图,矩形ABCD的对角线AC,BD交于点O,∠AOB=60°,AC=2,则边BC长为 .
 13. 梭梭树因其顽强的生命力和防风固沙的作用,被称为“沙漠植被之王”.新疆北部某沙漠2020年有16万亩梭梭树,经过两年的人工种植和自然繁殖,2022年达到25万亩,求这两年的平均增长率 .14. 若关于的一元二次方程有实数根,则实数的取值范围是 .15. 如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DH⊥BC于点H,连接OH,若OA=4, , 则OH的长为 .
13. 梭梭树因其顽强的生命力和防风固沙的作用,被称为“沙漠植被之王”.新疆北部某沙漠2020年有16万亩梭梭树,经过两年的人工种植和自然繁殖,2022年达到25万亩,求这两年的平均增长率 .14. 若关于的一元二次方程有实数根,则实数的取值范围是 .15. 如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DH⊥BC于点H,连接OH,若OA=4, , 则OH的长为 .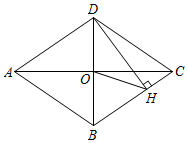 16. 如图,点F,G分别在正方形ABCD的边BC,CD上,E为AB中点,连结ED,正方形FGQP的边PQ恰好在DE上,记正方形ABCD面积为 , 正方形FPQG面积为 , 则的值为 .
16. 如图,点F,G分别在正方形ABCD的边BC,CD上,E为AB中点,连结ED,正方形FGQP的边PQ恰好在DE上,记正方形ABCD面积为 , 正方形FPQG面积为 , 则的值为 .
三、解答题
-
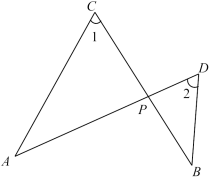
17. 解方程:(1)、;(2)、 .18. 如图,AD、BC相交于点P,连接AC、BD,且∠1=∠2,AC=3,CP=2,DP=1,求BD的长.
 19. 如图,点E,F分别在菱形ABCD的边BC,CD上,且∠BAE=∠DAF.求证:AE=AF.
19. 如图,点E,F分别在菱形ABCD的边BC,CD上,且∠BAE=∠DAF.求证:AE=AF.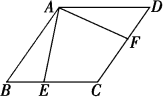 20. 如图,在一块长13m,宽7m的矩形空地上,修建同样宽的两条互相垂直的道路(两条道路分别与矩形的一条边平行),剩余部分栽种花草,若栽种花草的面积是 , 则道路的宽应设计为多少m?
20. 如图,在一块长13m,宽7m的矩形空地上,修建同样宽的两条互相垂直的道路(两条道路分别与矩形的一条边平行),剩余部分栽种花草,若栽种花草的面积是 , 则道路的宽应设计为多少m? 21. 如图,为矩形对角线的中点,于点 , 交 , 于点 , , 连接 , .
21. 如图,为矩形对角线的中点,于点 , 交 , 于点 , , 连接 , . (1)、求证:四边形为菱形;(2)、若 , , 求的长.22. 如图,正方形中,E,F分别是边 , 上的点, , , 连接并延长交的延长线于点G.
(1)、求证:四边形为菱形;(2)、若 , , 求的长.22. 如图,正方形中,E,F分别是边 , 上的点, , , 连接并延长交的延长线于点G. (1)、求证:;(2)、若正方形的边长为6,求的长.23. 某中学在艺术节期间向全校学生征集书画作品,美术王老师从全校随机抽取了四个班级记作A、B、C、D,对征集到的作品的数量进行了分析统计,制作了如下两幅不完整的统计图.
(1)、求证:;(2)、若正方形的边长为6,求的长.23. 某中学在艺术节期间向全校学生征集书画作品,美术王老师从全校随机抽取了四个班级记作A、B、C、D,对征集到的作品的数量进行了分析统计,制作了如下两幅不完整的统计图.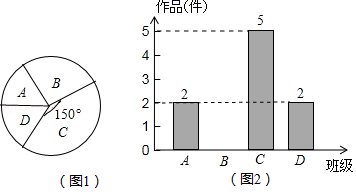 (1)、王老师抽查的四个班级共征集到作品多少件?(2)、请把图2的条形统计图补充完整;(3)、若全校参展作品中有四名同学获得一等奖,其中有二名男生、二名女生.现在要在其中抽两名同学去参加学校总结表彰座谈会,请用画树状图或列表的方法求恰好抽中一名男生一名女生的概率.24. 如图, , , , . 点P从点C出发,以的速度沿向点A匀速运动,同时点Q从点B出发,以的速度沿向点C匀速运动,设点P、Q运动时间为t,当一个点到达终点时,另一个点随之停止.
(1)、王老师抽查的四个班级共征集到作品多少件?(2)、请把图2的条形统计图补充完整;(3)、若全校参展作品中有四名同学获得一等奖,其中有二名男生、二名女生.现在要在其中抽两名同学去参加学校总结表彰座谈会,请用画树状图或列表的方法求恰好抽中一名男生一名女生的概率.24. 如图, , , , . 点P从点C出发,以的速度沿向点A匀速运动,同时点Q从点B出发,以的速度沿向点C匀速运动,设点P、Q运动时间为t,当一个点到达终点时,另一个点随之停止. (1)、求经过几秒后,的面积等于?(2)、经过几秒,与相似?(3)、①是否存在t,使得的面积等于?若存在,请求出t的值,若不存在,请说明理由;②设四边形的面积为S,请直接写出S的最大值或最小值.
(1)、求经过几秒后,的面积等于?(2)、经过几秒,与相似?(3)、①是否存在t,使得的面积等于?若存在,请求出t的值,若不存在,请说明理由;②设四边形的面积为S,请直接写出S的最大值或最小值.