山东省济南市市中区2022-2023学年九年级上学期期中数学试题
试卷更新日期:2022-12-20 类型:期中考试
一、单选题
-
1. 济南轨道交通4号线于2021年3月6日开工建设,如图是建设现场一个螺栓的示意图,它的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 某厂从生产的一批零件中抽取2000个进行质量检查,结果发现有10个是次品,那么从中任取1个是次品概率约为( )A、 B、 C、 D、3. 如图,直线 , 直线AC和DF被 , , 所截,AB=8,BC=12,EF=9,则DE的长为( )
2. 某厂从生产的一批零件中抽取2000个进行质量检查,结果发现有10个是次品,那么从中任取1个是次品概率约为( )A、 B、 C、 D、3. 如图,直线 , 直线AC和DF被 , , 所截,AB=8,BC=12,EF=9,则DE的长为( ) A、5 B、6 C、7 D、84. 若点A(-2,1)在反比例函数y=的图像上,则k的值是( )A、2 B、-2 C、 D、-5. 如图,中, , , 则等于( )
A、5 B、6 C、7 D、84. 若点A(-2,1)在反比例函数y=的图像上,则k的值是( )A、2 B、-2 C、 D、-5. 如图,中, , , 则等于( ) A、 B、 C、 D、6. 已知△ABC如图,则下列4个三角形中,与△ABC相似的是( )
A、 B、 C、 D、6. 已知△ABC如图,则下列4个三角形中,与△ABC相似的是( ) A、
A、 B、
B、 C、
C、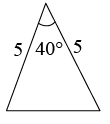 D、
D、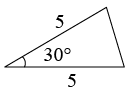 7. 如图,O为跷跷板AB的中点.支柱OC与地面MN垂直,垂足为点C,当跷跷板的一端B着地时,跷跷板AB与地面MN的夹角为20°,测得AB=1.6m,则OC的长为( )
7. 如图,O为跷跷板AB的中点.支柱OC与地面MN垂直,垂足为点C,当跷跷板的一端B着地时,跷跷板AB与地面MN的夹角为20°,测得AB=1.6m,则OC的长为( )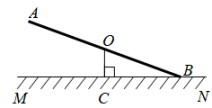 A、 B、 C、 D、8. 木板对地面的压强p(Pa)是木板面积S(m2)的反比例函数,其图象如图所示,当压强不超过400 Pa时,木板的面积应( )
A、 B、 C、 D、8. 木板对地面的压强p(Pa)是木板面积S(m2)的反比例函数,其图象如图所示,当压强不超过400 Pa时,木板的面积应( ) A、不大于1.5 m2 B、不小于1.5 m2 C、不大于m2 D、不小于m29. 如图,小明周末晚上陪父母在马路上散步,他由灯下A处前进4米到达B处时,测得影子长为1米,已知小明身高1.6米,他若继续往前走4米到达D处,此时影子长为( )
A、不大于1.5 m2 B、不小于1.5 m2 C、不大于m2 D、不小于m29. 如图,小明周末晚上陪父母在马路上散步,他由灯下A处前进4米到达B处时,测得影子长为1米,已知小明身高1.6米,他若继续往前走4米到达D处,此时影子长为( )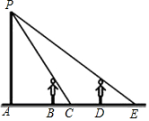 A、1米 B、2米 C、3米 D、4米10. 谢尔宾斯基地毯是由波兰数学家谢尔宾斯基提出的一种具有“自相似”性质的分形图形:将第1个正方形分成9等份(如图①),挖去中间的小正方形,得到第2个正方形(如图②);再将余下的8个小正方形分成9等份,挖去中间的小正方形,得到第3个正方形(如图③);…这样继续进行下去,就得到空格子越来越多的谢尔宾斯基地毯.若图①中大正方形的边长为1,则第4个正方形中阴影部分的面积是( )
A、1米 B、2米 C、3米 D、4米10. 谢尔宾斯基地毯是由波兰数学家谢尔宾斯基提出的一种具有“自相似”性质的分形图形:将第1个正方形分成9等份(如图①),挖去中间的小正方形,得到第2个正方形(如图②);再将余下的8个小正方形分成9等份,挖去中间的小正方形,得到第3个正方形(如图③);…这样继续进行下去,就得到空格子越来越多的谢尔宾斯基地毯.若图①中大正方形的边长为1,则第4个正方形中阴影部分的面积是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算: .12. 若 ,则 = .13. 如果小球在如图所示的地板上自由地滚动,并随机停留在某块方砖上,那么小球最终停留在黑色区域的概率是 .
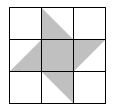 14. 如图所示, 是放置在正方形网格中的一个角,则 的值是.
14. 如图所示, 是放置在正方形网格中的一个角,则 的值是. 15. 如图,平行四边形OABC的边OA在x轴上,顶点C在反比例函数的图像上,BC与y轴相交于点D,且D为BC的中点,若平行四边形OABC的面积为8,则k= .
15. 如图,平行四边形OABC的边OA在x轴上,顶点C在反比例函数的图像上,BC与y轴相交于点D,且D为BC的中点,若平行四边形OABC的面积为8,则k= . 16. 如图,在边长为2的正方形ABCD中,点E为AD的中点,将△CDE沿CE翻折得△CME,点M落在四边形ABCE内.点N为线段CE上的动点,过点N作NP//EM交MC于点P,则MN+NP的最小值为.
16. 如图,在边长为2的正方形ABCD中,点E为AD的中点,将△CDE沿CE翻折得△CME,点M落在四边形ABCE内.点N为线段CE上的动点,过点N作NP//EM交MC于点P,则MN+NP的最小值为.

三、解答题
-
17. 计算:+2tan60°+(-3)0-;18. 在如图的方格纸中,的顶点坐标分别为 , , , 与是关于点P为位似中心的位似图形.
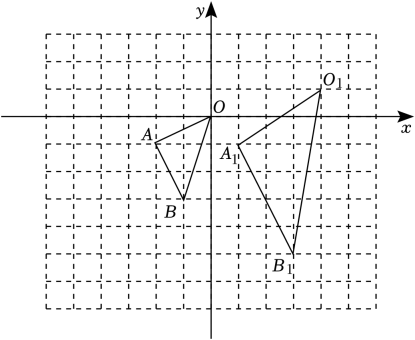
( 1 )在图中标出位似中心P的位置并直接写出点P的坐标为 .
( 2 )以原点O为位似中心,在位似中心的同侧画出的一个位似 , 使它与的位似比为2:1;
( 3 )的内部一点M的坐标为 , 直接写出点M在中的对应点的坐标为 .
19. 如图,BD、AC相交于点P,连接BC、AD,且∠1=∠2,若PB=3,PC=1,PD=2,求PA的长度. 20. 如图,已知点 , 是直线与反比例函数图像的交点,且该直线与y轴交于点C.
20. 如图,已知点 , 是直线与反比例函数图像的交点,且该直线与y轴交于点C. (1)、填空:b= ;m= ;k= ;(2)、连接 , 求的面积;(3)、根据图像,直接写出不等式时x的取值范围.21. 在一个不透明的袋子里装有只有颜色不同的黑、白两种颜色的球共50个,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
(1)、填空:b= ;m= ;k= ;(2)、连接 , 求的面积;(3)、根据图像,直接写出不等式时x的取值范围.21. 在一个不透明的袋子里装有只有颜色不同的黑、白两种颜色的球共50个,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:摸球的次数n
100
200
300
500
800
1000
摸到黑球的次数m
摸到黑球的频率
(1)、填空:a= ;当n很大时,摸到黑球的频率将会趋近(精确到0.1);(2)、某小组成员从袋中拿出1个黑球,3个白球放入一个新的不透明袋子中,随机摸出两个球,请你用列表或树状图的方法求出随机摸出的两个球颜色不同的概率.22. 北京时间2022年6月5日10时44分,搭载神舟十四号载人飞船的长征二号F遥十四运载火箭在酒泉卫星发射中心点火发射,约秒后,神舟十四号载人飞船与火箭成功分离,进入预定轨道,顺利将陈东、蔡旭哲、刘洋3名航天员送入太空.如图是模拟的火箭发射装置示意图,一枚运载火箭从地面L处发射,当火箭到达A点时,从位于地面R处的雷达站测得的距离是 , 仰角为;约后火箭到达B点,此时测得仰角为(参考数据: , , ). (1)、求地面雷达站R到发射处L的水平距离.(2)、求这枚火箭从A到B的平均速度是多少千米/秒?23. 小明和几位同学做手的影子游戏时,发现对于同一物体,影子的大小与光源到物体的距离有关.因此,他们认为:可以借助物体的影子长度计算光源到物体的位置.于是,他们做了以下尝试.
(1)、求地面雷达站R到发射处L的水平距离.(2)、求这枚火箭从A到B的平均速度是多少千米/秒?23. 小明和几位同学做手的影子游戏时,发现对于同一物体,影子的大小与光源到物体的距离有关.因此,他们认为:可以借助物体的影子长度计算光源到物体的位置.于是,他们做了以下尝试. (1)、如图1,垂直于地面放置的正方形框架 , 边长为 , 在其上方点P处有一灯泡,在灯泡的照射下,正方形框架的横向影子 , 的长度和为 . 那么灯泡离地面的高度为多少.(2)、不改变图1中灯泡的高度,将两个边长为的正方形框架按图2摆放,请计算此时横向影子 , 的长度和为多少?24.
(1)、如图1,垂直于地面放置的正方形框架 , 边长为 , 在其上方点P处有一灯泡,在灯泡的照射下,正方形框架的横向影子 , 的长度和为 . 那么灯泡离地面的高度为多少.(2)、不改变图1中灯泡的高度,将两个边长为的正方形框架按图2摆放,请计算此时横向影子 , 的长度和为多少?24.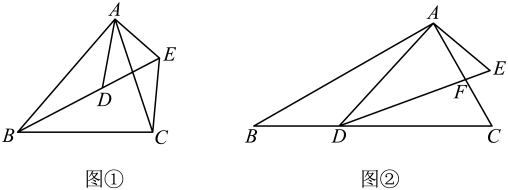 (1)、 [问题背景]如图①,已知 , 求证: .(2)、[尝试应用]如图②,在和中, , , 与相交于点F,点D在边上, .
(1)、 [问题背景]如图①,已知 , 求证: .(2)、[尝试应用]如图②,在和中, , , 与相交于点F,点D在边上, .①填空:;
②求的值.
25. 如图,在平面直角坐标系中,、是矩形的两个顶点,点D是线段上的一个动点(不与重合),双曲线()经过点D,与矩形的边相交于点E.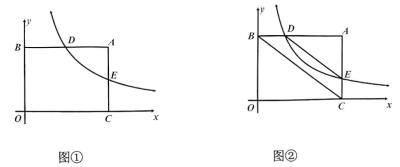
 (1)、如图①,当点D为中点时,k的值为 , 点E的坐标为;(2)、如图②,当点D在线段上的任意位置时(不与重合),连接 , 求证:;(3)、是否存在反比例函数上不同于点D的一点F,满足:为直角三角形, , 且 , 若存在,请直接写出满足以上条件时点D的横坐标,若不存在,请说明理由.26. 如图①,已知在正方形中,点E是边的中点,以为斜边构造等腰直角 , 将绕点B在平面内作逆时针旋转.
(1)、如图①,当点D为中点时,k的值为 , 点E的坐标为;(2)、如图②,当点D在线段上的任意位置时(不与重合),连接 , 求证:;(3)、是否存在反比例函数上不同于点D的一点F,满足:为直角三角形, , 且 , 若存在,请直接写出满足以上条件时点D的横坐标,若不存在,请说明理由.26. 如图①,已知在正方形中,点E是边的中点,以为斜边构造等腰直角 , 将绕点B在平面内作逆时针旋转. (1)、如图②,当时,若 , 则; ;(2)、如图③,延长 , 与分别相交于点 , 延长 , 与分别相交于点 , 求证:;(3)、如图④,连接 , 请直接写出当取得最小值时,的正切值.
(1)、如图②,当时,若 , 则; ;(2)、如图③,延长 , 与分别相交于点 , 延长 , 与分别相交于点 , 求证:;(3)、如图④,连接 , 请直接写出当取得最小值时,的正切值.