山东省济南市平阴县2022-2023学年九年级上学期期中数学试题

试卷更新日期：2022-12-20 类型：期中考试

进入出卷网下载

一、单选题

1. 下列方程为一元二次方程的是（）

A、x+2y＝1 B、x²-2＝0 C、x＝2x³+3 D、3x+ $\frac{1}{x}$ ＝1

查看试题解析
2. 已知 $x = 1$ 是方程 $x^{2} + a x + 2 = 0$ 的一个根，则方程的另一个根为（）

A、-2 B、2 C、-3 D、3

查看试题解析
3. 一元二次方程 $x^{2} + 4 x - 5 = 0$ 经过配方后，可变形为（）

A、 ${(x - 2)}^{2} = 1$ B、 ${(x + 2)}^{2} = - 1$ C、 ${(x + 2)}^{2} = 9$ D、 ${(x - 2)}^{2} = 9$

查看试题解析
4. 已知 $\frac{b}{a} = \frac{5}{9}$ ，则 $\frac{a - b}{a}$ 的值是（）

A、 $\frac{2}{3}$ B、 $\frac{3}{2}$ C、 $\frac{9}{4}$ D、 $\frac{4}{9}$

查看试题解析
5. 若 $△ A B C ∽ △ D E F$ ，其相似比为 $2 ： 3$ ，则 $△ A B C$ 与 $△ D E F$ 的面积比为（）

A、 $2 ： 3$ B、 $3 ： 2$ C、 $4 ： 9$ D、 $16 ： 81$

查看试题解析
6. 一本书的宽与长之比为黄金比，书的宽为14cm，则它的长为（　　）cm

A、 $7 \sqrt{5} + 7$ B、 $21 - 7 \sqrt{5}$ C、 $7 \sqrt{5} - 7$ D、 $7 \sqrt{5} - 21$

查看试题解析
7. 已知反比例函数 $y = \frac{3}{x}$ ，下列结论中错误的是 $($ $)$

A、其图象经过点 $(3 ， 1)$ B、其图象分别位于第一、第三象限 C、当 $x > 0$ 时，y随x的增大而减小 D、当 $x > 1$ 时， $y > 3$

查看试题解析
8. 如图，电路图上有四个开关A、B、C、D和一个小灯泡，闭合开关D或同时闭合开关A、B、C都可使小灯泡发光，则任意闭合其中两个开关，小灯泡发光的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{6}$

查看试题解析
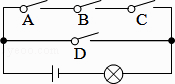9. 函数 $y = a x + a$ 与 $y = \frac{a}{x} (a \neq 0)$ 在同一坐标系中的图象可能是（）

A、 B、 C、 D、

查看试题解析
10.
在边长为1的4×4方格上建立直角坐标系（如图甲），在第一象限内画出反比例函数 $y = \frac{16}{x}$ 、 $y = \frac{6}{x}$ 、 $y = \frac{4}{x}$ 的图象，它们分别经过方格中的一个格点、二个格点、三个格点；在边长为1的10×10方格上建立直角坐标系（如图乙），在第一象限内画出反比例函数的图象，使它们经过方格中的三个或四个格点，则最多可画出几条( )

A、12 B、13 C、25 D、50

查看试题解析

二、填空题

11. 在一个不透明的口袋中，装有若干个红球和8个黄球，它们除颜色外没有任何区别，摇匀后从中随机摸出一个球，记下颜色后再放回口袋中，通过大量重复摸球试验发现，摸到黄球的频率0.4，则估计盒子中大约有红球个.

查看试题解析
12. 若一元二次方程 $2 x^{2} - 4 x + m = 0$ 有两个相等的实数根，则m= ．

查看试题解析
13. 某厂家今年一月份的口罩产量是30万个，三月份的口罩产量是50万个，若设该厂家一月份到三月份的口罩产量的月平均增长率为x．则所列方程为

查看试题解析
14.
如图，小明在打网球时，使球恰好能打过网，而且落在离网4米的位置上，则球拍击球的高度h为．

查看试题解析
15. 如图，正方形 $A B C D$ 的边长为5，点A的坐标为 $(4 ， 0)$ ，点B在y轴上，若反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象过点C，则k的值为．

查看试题解析
16. $∠ B A C = 90 °$ ， $A B = A C = 4$ ，点D是边 $B C$ 上一动点（不与B，C重合）， $∠ A D E = 45 °$ ， $D E$ 交 $A C$ 于点E，下列结论：① $△ A D E$ 与 $△ A C D$ 一定相似；② $△ A B C$ 与 $△ D C E$ 一定相似；③当 $A D = 3$ 时， $C E = \frac{7}{4}$ ；④ $0 < C E \leq 2$ ．其中正确的结论有（填写序号）

查看试题解析

三、解答题

17. 解下列方程：

(1)、 $x^{2} - 4 x - 3 = 0$ ；

(2)、 $2 x (x + 1) = x + 1$ ．

查看试题解析
18. 如图，在平行四边形 $A B C D$ 中，E为 $A B$ 边上一点，连接 $C E$ ， F为 $C E$ 上一点，且 $∠ D F C = ∠ B$ ．求证： $△ D C F ∽ △ C E B$ ．

查看试题解析
19. 如图，在平面直角坐标系中， $△ A B C$ 的三个顶点坐标分别为 $A (- 2 ， 1)$ ， $B (- 1 ， 4)$ ， $C (- 3 ， 2)$ ．

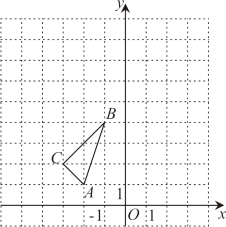(1)、以原点O为位似中心，位似比为 $1 ： 2$ ，在y轴的左侧，画出 $△ A B C$ 放大后的图形 $△ A_{1} B_{1} C_{1}$ ；

(2)、直接写出 $C_{1}$ 点坐标．

查看试题解析
20. 阅读下面的材料：
如果函数y＝f（x）满足：对于自变量x取值范围内的任意x₁ ， x₂ ，
①若x₁＜x₂ ，都有f（x₁）＜f（x₂），则称f（x）是增函数；
②若x₁＜x₂ ，都有f（x₁）＞f（x₂），则称f（x）是减函数．
例题：证明函数f（x）＝x²（x＞0）是增函数．
证明：任取x₁＜x₂ ，且x₁＞0，x₂＞0．
则f（x₁）-f（x₂）＝x₁²-x₂²＝（x₁+x₂）（x₁-x₂）．
∵x₁＜x₂且x₁＞0，x₂＞0，
∴x₁+x₂＞0，x₁-x₂＜0．
∴（x₁+x₂）（x₁-x₂）＜0，即f（x₁）-f（x₂）＜0，f（x₁）＜f（x₂）．
∴函数f（x）＝x²（x＞0）是增函数．
根据以上材料解答下列问题：

(1)、函数f（x） $= \frac{1}{x}$ （x＞0），f（1） $= \frac{1}{1} =$ 1，f（2） $= \frac{1}{2}$ ， f（3）＝， f（4）＝；

(2)、猜想f（x） $= \frac{1}{x}$ （x＞0）是函数（填“增”或“减”），并证明你的猜想．

查看试题解析
21. 教师办公室有一种可以自动加热的饮水机，该饮水机的工作程序是：放满水后接通电源，则自动开始加热，每分钟水温上升10℃，待加热到100℃，饮水机自动停止加热，水温开始下降．水温y（℃）和通电时间x（min）成反比例函数关系，直至水温降至室温，饮水机再次自动加热，重复上述过程．设某天水温和室温均为20℃，接通电源后，水温y（℃）和通电时间x（min）之间的关系如图所示，回答下列问题：

(1)、分别求出当0≤x≤8和8＜x≤a时，y和x之间的函数关系式；

(2)、求出图中a的值；

(3)、李老师这天早上7：30将饮水机电源打开，若他想在8：10上课前喝到不低于40℃的开水，则他需要在什么时间段内接水？

查看试题解析
22. 李老师为缓解小如和小意的压力，准备了四个完全相同（不透明）的锦囊，里面各装有一张纸条，分别写有：A．转移注意力，B．合理宣泄，C．自我暗示，D．放松训练．

(1)、若小如随机取走一个锦囊，则取走的是写有“自我暗示”的概率是；

(2)、若小如和小意每人先后随机抽取一个锦囊（取走后不放回），请用列表法或画树状图的方法求小如和小意都没有取走“合理宣泄”的概率．

查看试题解析
23. 某公司设计了一款工艺品，每件的成本是40元，为了合理定价，投放市场进行试销：据市场调查，销售单价是50元时，每天的销售量是100件，而销售单价每提高1元，每天就减少售出2件，但要求销售单价不得超过65元．

(1)、若销售单价为每件52元，求每天的销售利润；

(2)、要使每天销售这种工艺品盈利1350元，那么每件工艺品售价应为多少元？

查看试题解析
24. 如图，在直角三角形ABC中，直角边 $A C = 3 c m$ ， $B C = 4 c m$ ．设P，Q分别为AB、BC上的动点，在点P自点A沿AB方向向B作匀速移动的同时，点Q自点B沿BC方向向点C作匀速移动，它们移动的速度均为每秒1cm，当Q点到达C点时，P点就停止移动．设P，Q移动的时间t秒．

(1)、当t为何值时， $△ P B Q$ 是以 $∠ B$ 为顶角的等腰三角形？

(2)、 $△ P B Q$ 能否与直角三角形ABC相似？若能，求t的值；若不能，说明理由．

查看试题解析
25. 如图，在平面直角坐标系中，直线 $y_{1} = k_{1} x + b$ 与双曲线 $y_{2} = \frac{k_{2}}{x}$ 相交于 $A (- 2 ， 3) ， B (m ， - 2)$ 两点．

(1)、求 $y_{1} ， y_{2}$ 对应的函数表达式；

(2)、过点B作 $B P / / x$ 轴交y轴于点P，求 $△ A B P$ 的面积；

(3)、根据函数图象，直接写出关于x的不等式 $k_{1} x + b < \frac{k_{2}}{x}$ 的解集．

查看试题解析
26.

(1)、【问题背景】如图，在 $R t △ A B C$ 和 $R t △ A D E$ 中， $A B = A C ， A D = A E$ ，由已知可以得到：
① $△$ $≌ △$ ；

② $△$ $∽ △$ ．

(2)、【尝试应用】如图，在 $△ A B C$ 和 $△ A D E$ 中， $∠ A C B = ∠ A E D = 90 ° ， ∠ A B C = ∠ A D E = 30 °$ ，
求证： $△ A C E ∽ △ A B D$ ．

(3)、【问题解决】如图，在 $△ A B C$ 和 $△ A D E$ 中， $∠ B A C = ∠ D A E = 90 ° ， ∠ A B C = ∠ A D E = 30 ° ， A C$ 与 $D E$ 相交于点F，点D在 $B C$ 上， $\frac{A D}{B D} = \sqrt{3}$ ，求 $\frac{D F}{C F}$ 的值．

查看试题解析