山东省济南市槐荫区2022-2023学年九年级上学期期中数学试题
试卷更新日期:2022-12-20 类型:期中考试
一、单选题
-
1. 3tan60°的值为()A、 B、 C、 D、32. 若 ,则 的值为( )A、1 B、 C、 D、3. 如图,四边形ABCD∽四边形EFGH,∠A=80°,∠C=90°,∠F=70°,则∠H的度数为( )
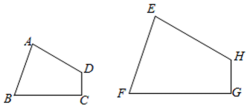 A、70° B、80° C、110° D、120°4. 如图,直线 , 直线和被直线、、所截, , , , 则的长为( )
A、70° B、80° C、110° D、120°4. 如图,直线 , 直线和被直线、、所截, , , , 则的长为( ) A、2 B、 C、 D、5. 反比例函数经过点 , 则下列说法错误的是( )A、函数图象经过点 B、函数图象分布在第一、三象限 C、当时,y随x的增大而增大 D、当时,y随x的增大而减小6. 如图所示,给出下列条件:
A、2 B、 C、 D、5. 反比例函数经过点 , 则下列说法错误的是( )A、函数图象经过点 B、函数图象分布在第一、三象限 C、当时,y随x的增大而增大 D、当时,y随x的增大而减小6. 如图所示,给出下列条件:① ;② ;③ ;④ ;⑤
其中单独能够判定 的个数为( )
 A、2 B、3 C、4 D、57. 如图,在平面直角坐标系xOy中,函数y=kx+b(k≠0)与y= (m≠0)的图象相交于点A(-2,3),B(6,-1),则不等式kx+b> 的解集为( )
A、2 B、3 C、4 D、57. 如图,在平面直角坐标系xOy中,函数y=kx+b(k≠0)与y= (m≠0)的图象相交于点A(-2,3),B(6,-1),则不等式kx+b> 的解集为( ) A、 B、 或 C、 D、 或8. 如图,电线杆的高度为CD=m,两根拉线AC与BC互相垂直(A,D,B在同一条直线上),若∠CBA=α,则拉线AC的长度可以表示为( )
A、 B、 或 C、 D、 或8. 如图,电线杆的高度为CD=m,两根拉线AC与BC互相垂直(A,D,B在同一条直线上),若∠CBA=α,则拉线AC的长度可以表示为( )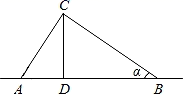 A、 B、 C、mcosα D、9. 如图,已知双曲线与矩形的对角线相交于点D,若 , 矩形的面积为 , 则k等于( )
A、 B、 C、mcosα D、9. 如图,已知双曲线与矩形的对角线相交于点D,若 , 矩形的面积为 , 则k等于( ) A、6 B、12 C、24 D、3610. 如图,正方形 ,点 在边 上,且 , ,垂足为 ,且交 于点 , 与 交于点 ,延长 至 ,使 ,连接 .有如下结论:① ;② ;③ ;④ .上述结论中,所有正确结论的序号是( )
A、6 B、12 C、24 D、3610. 如图,正方形 ,点 在边 上,且 , ,垂足为 ,且交 于点 , 与 交于点 ,延长 至 ,使 ,连接 .有如下结论:① ;② ;③ ;④ .上述结论中,所有正确结论的序号是( )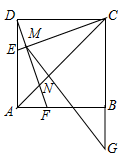 A、①② B、①③ C、①②③ D、②③④
A、①② B、①③ C、①②③ D、②③④二、填空题
-
11. 近视眼镜的度数y(度)与镜片焦距x(米)成反比例,已知400度近视镜片的焦距为0.2米,则眼镜度数y与镜片焦距x之间的函数关系式是 .
12. 在中, , , 则的值为 .13. 如图,小强自制了一个小孔成像装置,其中纸筒的长度为15cm.他准备了一支长为20cm的蜡烛,想要得到高度为5cm的像.蜡烛应放在距离纸筒 cm的地方. 14. 如图,点A是反比例函数图象上一点,过点A作AB⊥y轴于点D,且点D为线段AB的中点.若点C为x轴上任意一点,且△ABC的面积为4,则k= .
14. 如图,点A是反比例函数图象上一点,过点A作AB⊥y轴于点D,且点D为线段AB的中点.若点C为x轴上任意一点,且△ABC的面积为4,则k= .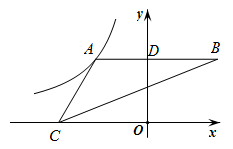 15. 如图,的顶点都在正方形网格纸的格点上,则 .
15. 如图,的顶点都在正方形网格纸的格点上,则 .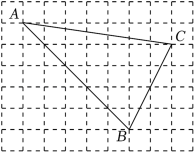 16. 如图,在直角坐标系中,矩形与矩形位似,矩形的边在y轴上,点B的坐标为 , 矩形的两边都在坐标轴上,且点F的坐标为 , 则矩形与的位似中心的坐标是 .
16. 如图,在直角坐标系中,矩形与矩形位似,矩形的边在y轴上,点B的坐标为 , 矩形的两边都在坐标轴上,且点F的坐标为 , 则矩形与的位似中心的坐标是 .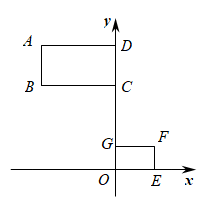
三、解答题
-
17. 计算:18. 如图,在中, , , , 求AC的长和的值.
 19. 如图,在边长为4的正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点,求证:△ADQ∽△QCP.
19. 如图,在边长为4的正方形ABCD中,P是BC上的点,且BP=3PC,Q是CD的中点,求证:△ADQ∽△QCP. 20. 如图,已知点O是坐标原点,A、B两点的坐标分别为
20. 如图,已知点O是坐标原点,A、B两点的坐标分别为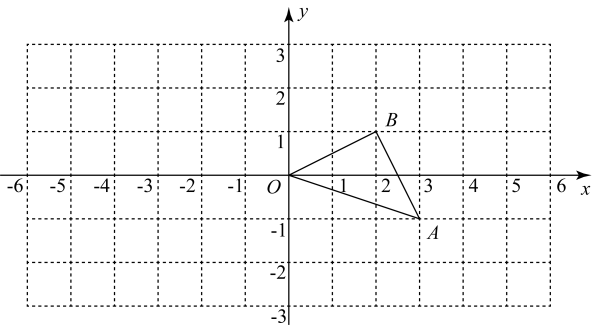 (1)、以O点为位似中心在y轴的左侧将放大到原图的2倍,画出对应的 , 并写出点A的对应点的坐标;(2)、直接写出的面积.21. 如图,反比例函数的图象与正比例函数的图象交于、B两点.点在反比例函数图象上,连接 , 交y轴于点N.
(1)、以O点为位似中心在y轴的左侧将放大到原图的2倍,画出对应的 , 并写出点A的对应点的坐标;(2)、直接写出的面积.21. 如图,反比例函数的图象与正比例函数的图象交于、B两点.点在反比例函数图象上,连接 , 交y轴于点N. (1)、求反比例函数的解析式.(2)、求的面积.22. 如图,、是的高,连接 .
(1)、求反比例函数的解析式.(2)、求的面积.22. 如图,、是的高,连接 . (1)、求证:∽;(2)、若点D是的中点, , , 求的长.23. 有这样一个问题:探究函数的图象与性质.
(1)、求证:∽;(2)、若点D是的中点, , , 求的长.23. 有这样一个问题:探究函数的图象与性质.小亮根据学习函数的经验,对函数的图象与性质进行了探究.
下面是小亮的探究过程,请补充完整:
(1)、函数中自变量x的取值范围是;(2)、下表是y与x的几组对应值,请直接写出m的值;…
-2
-1
0
1
3
4
5
6
…
…
0
m
…
(3)、在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象; (4)、根据画出的函数图象,发现下列特征:
(4)、根据画出的函数图象,发现下列特征:①该函数的图象是中心对称图形,对称中心的坐标是;
②该函数的图象与直线x=2越来越靠近而永不相交,该函数的图象还与直线越来越靠近而永不相交.
24. 济南黄河大桥位于济南北郊,该桥于1982年7月建成通车,至今已40年整,大桥总长米,是当时亚洲跨径最大的桥梁,在当时世界十大预应力混凝土斜拉桥中排行第8位.某校数学“综合与实践”小组的同学利用课余时间按照如图所示的测量示意图对该桥进行了实地测量,测得如下数据: , 垂直高度米.
 (1)、求的长(保留根号);(2)、若要在最长的斜拉链条和斜塔上装节能灯带,灯带每米造价200元,求斜拉链条和斜塔上灯带的总造价是多少元?(取 , , )25. 如图1,在Rt△ABC中,∠BAC=90°,AB=AC,D,E两点分别在AC,BC上,且DE∥AB,将△CDE绕点C按顺时针方向旋转,记旋转角为α.
(1)、求的长(保留根号);(2)、若要在最长的斜拉链条和斜塔上装节能灯带,灯带每米造价200元,求斜拉链条和斜塔上灯带的总造价是多少元?(取 , , )25. 如图1,在Rt△ABC中,∠BAC=90°,AB=AC,D,E两点分别在AC,BC上,且DE∥AB,将△CDE绕点C按顺时针方向旋转,记旋转角为α. (1)、问题发现:当α=0°时,的值为;(2)、拓展探究:当0°≤α<360°时,若△EDC旋转到如图2的情况时,求出的值;(3)、问题解决:当△EDC旋转至A,B,E三点共线时,若设CE=5,AC=4,直接写出线段BE的长 .26. 一次函数y=kx+b的图象与x轴交于A(﹣2,0),图象过点B(4,n),BC⊥x轴于点C,已知tanB=2,y=kx+b与反比例函数y(x>0)的图象交于点E(a,2),点P是线段AB边上的动点.
(1)、问题发现:当α=0°时,的值为;(2)、拓展探究:当0°≤α<360°时,若△EDC旋转到如图2的情况时,求出的值;(3)、问题解决:当△EDC旋转至A,B,E三点共线时,若设CE=5,AC=4,直接写出线段BE的长 .26. 一次函数y=kx+b的图象与x轴交于A(﹣2,0),图象过点B(4,n),BC⊥x轴于点C,已知tanB=2,y=kx+b与反比例函数y(x>0)的图象交于点E(a,2),点P是线段AB边上的动点. (1)、分别求直线AB的解析式和反比例函数的解析式;(2)、连接OD,OE,求的值;(3)、是否存在点P,使得△BCP与△BDE相似?若存在,求出此时点P的坐标;若不存在,请说明理由.
(1)、分别求直线AB的解析式和反比例函数的解析式;(2)、连接OD,OE,求的值;(3)、是否存在点P,使得△BCP与△BDE相似?若存在,求出此时点P的坐标;若不存在,请说明理由.