山东省菏泽市郓城县2022-2023学年九年级上学期期中数学试题

试卷更新日期：2022-12-20 类型：期中考试

进入出卷网下载

一、单选题

1. 已知关于x的方程：(1)ax²+bx+c=0；(2)x²-4x=8+x²；(3)1+(x-1)(x+1)=0；(4)(k²+1)x²+kx+1=0中，一元二次方程的个数为(　　)

A、1 B、2 C、3 D、4

查看试题解析
2. 我市某楼盘准备以每平方6000元的均价对外销售，由于国务院有关房地产的新政策出台后，购房者持币观望，为了加快资金周转，房地产开发商对价格经过连续两次下调后，决定以每平方4860元的均价开盘销售，则平均每次下调的百分率是（）.

A、8% B、9% C、10% D、11%

查看试题解析
3. 在一个不透明的口袋中，装有若干个红球和4个黄球，它们除颜色外没有任可其他区别，摇匀后从中随机摸出一个球，记下颜色后再放回口袋中，通过大量重复摸球实验发现，摸到黄球的频率是0.2，则估计盒子中大约有红球（）

A、16个 B、20个 C、25个 D、30个

查看试题解析
4. “田忌赛马”的故事家喻户晓，若田忌出马的顺序一直是下等马、中等马、上等马（上等马跑得最快，中等马次之，下等马跑得最慢），而齐王随机出马，则田忌获胜（三局两胜则为胜）的可能性是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{6}$

查看试题解析
5. 如图，在菱形 $A B C D$ 中， $A C$ 与 $B D$ 相交于点O， $B C$ 的垂直平分线 $E F$ 分别交 $B C$ ， $A C$ 于点E，F，连接 $D F$ ，若 $∠ B C D = 70 °$ ，则 $∠ A D F$ 的度数是（）

A、60° B、75 C、80° D、110°

查看试题解析
6. 如图，在平面直角坐标系中，四边形 $O A B C$ 是矩形， $O A = 6$ ，将 $Δ A B C$ 沿直线 $A C$ 翻折，使点 $B$ 落在点 $D$ 处， $A D$ 交 $x$ 轴于点 $E$ ，若 $∠ B A C = 30 °$ ，则点 $D$ 的坐标为（）

A、 $(3 \sqrt{3} ， - 2)$ B、 $(3 \sqrt{3} ， - 3)$ C、 $(\sqrt{3} ， - 3)$ D、 $(3 ， - 3 \sqrt{3})$

查看试题解析
7. 如图 $l_{1} ∥ l_{2} ∥ l_{3}$ ，直线AC与DF交于点O，且与 $l_{1}$ ， $l_{2}$ ， $l_{3}$ 分别交于点A，B，C，D，E，F，则下列比例式错误的是（　　　）

A、 $\frac{A B}{B C} = \frac{D E}{E F}$ B、 $\frac{A B}{B O} = \frac{D E}{E O}$ C、 $\frac{O B}{O C} = \frac{O E}{O F}$ D、 $\frac{A D}{C F} = \frac{A O}{A C}$

查看试题解析
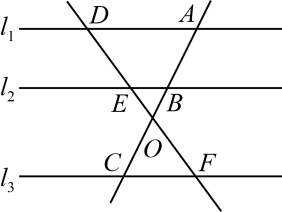8. 如图，四边形ABCD和 $A^{'} B^{'} C^{'} D^{'}$ 是以点O为位似中心的位似图形，若OA：OA′＝2：3，则四边形ABCD与四边形 $A^{'} B^{'} C^{'} D^{'}$ 的面积比为（　　）

A、4：9 B、2：5 C、2：7 D、2：3

查看试题解析

二、填空题

9. 若关于x的方程 $x^{2} + 5 x + k = 0$ 的一个根是1，则k的值为.

查看试题解析
10. 对于实数a，b，定义运算“※”如下：a※b=a²﹣ab，例如，5※3=5²﹣5×3=10．若（x+1）※（x﹣2）=6，则x的值为．

查看试题解析
11. 如图，在正方形 $A B C D$ 中，点F为 $C D$ 上一点， $B F$ 与 $A C$ 交于点E．若 $∠ C B F = 18 °$ ，则 $∠ A E D$ 等于度．

查看试题解析
12. 让图中两个转盘分别自由转动一次，当转盘停止转动时，两个指针分别落在某两个数所表示的区域，则这两个数的和是2的倍数或是3的倍数的概率等于．

查看试题解析
13. 如图是一位同学用激光笔测量某古城墙高度的示意图.点P处放一水平的平面镜，光线从点A出发经平面镜反射后刚好到古城墙 $C D$ 的顶端C处，若 $A B ⊥ B D$ ， $C D ⊥ B D$ ，测得 $A B = 1.5 m$ ， $B P = 2 m$ ， $P D = 6 m$ ，则该古城墙的高度 $C D$ 是 $m$ .

查看试题解析
14. 如图，D、E分别是△ABC的边AB、BC上的点，DE∥AC，若S_△_BDE：S_△_CDE＝1：3，则S_△_DOE：S_△_AOC的值为.

查看试题解析

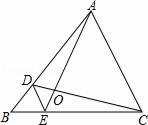
三、解答题

15. 用适当的方法解下列方程．

(1)、 $x^{2} - 2 x - 8 = 0$

(2)、 $x (x - 1) + 2 (x - 1) = 0$

查看试题解析
16. 已知关于x的一元二次方程x²+(2m+1)x+m²−2=0．

(1)、若该方程有两个实数根，求m的最小整数值；

(2)、若方程的两个实数根为x₁ ， x₂ ，且 ${(x_{1} - x_{2})}^{2} + m^{2} = 21$ ，求m的值．

查看试题解析
17. 一个口袋中有9个红球和若干个白球，在不允许将球倒出来数的前提下，小明采用如下的方法估算其中白球的个数：从口袋中随机摸出一球，记下颜色，然后把它放回口袋中，摇匀后再随机摸出一球，记下颜色…，小明重复上述过程共摸了100次，其中40次摸到白球，请回答：

(1)、口袋中的白球约有多少个？

(2)、有一个游乐场，要按照上述红球、白球的比例配置彩球池，若彩球池里共有1200个球，则需准备多少个红球？

查看试题解析
18. 如图，在矩形 $A B C D$ 中，点E，F分别在边 $A B ， B C$ 上， $A F ⊥ D E$ ，且 $A F = D E$ ， $A F$ 与 $D E$ 相交于点G．求证：矩形 $A B C D$ 为正方形；

查看试题解析
19. 在 $▱ A B C D$ 中，E、F分别是边BC，AD的中点，AC是对角线，过点D作DP $∥$ AC，交BA的延长线于点P，∠P=90°．求证：四边形AECF是菱形．

查看试题解析
20. 为了提高学生的阅读能力，我市某校开展了“读好书，助成长”的活动，并计划购置一批图书，购书前，对学生喜欢阅读的图书类型进行了抽样调查，并将调查数据绘制成两幅不完整的统计图，如图所示，请根据统计图回答下列问题：

(1)、本次调查共抽取了名学生，两幅统计图中的m＝， n＝．

(2)、已知该校共有3600名学生，请你估计该校喜欢阅读“A”类图书的学生约有多少人？

(3)、学校将举办读书知识竞赛，九年级1班要在本班3名优胜者（2男1女）中随机选送2人参赛，请用列表或画树状图的方法求被选送的两名参赛者为一男一女的概率．

查看试题解析
21. 如图，在 $R t △ A B C$ 中， $∠ A B C = 90 °$ ， E是边AC上一点，且 $B E = B C$ ，过点A作BE的垂线，交BE的延长线于点D，求证： $△ A D E ∽ △ A B C$ ．

查看试题解析
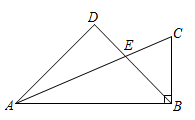22. 如图，等边三角形△ACB的边长为3，点P为BC上的一点，点D为AC上的一点，连接AP、PD，∠APD=60°．

(1)、求证：△ABP∽△PCD；

(2)、若PC=2，求CD的长．

查看试题解析
23. 某水果商场经销一种高档水果，原价每千克50元．连续两次降价后每千克32元，若每次下降的百分率相同．

(1)、求每次下降的百分率；

(2)、若每千克盈利10元，每天可售出500千克，经市场调查发现，在进货价不变的情况下，商场决定采取适当的涨价措施，若每千克涨价1元，日销售量将减少20千克，现该商场要保证每天盈利6000元，那么每千克应涨价多少元？

查看试题解析
24. 如图，在Rt $△ A B C$ 中， $∠ B = 90 °$ ， $A B = 6 c m$ ， $B C = 8 c m$ ，点P从点A出发，以1cm/s的速度沿AB运动；同时，点Q从点B出发，以2cm/s的速度沿BC运动．当点Q到达点C时，P、Q两点同时停止运动．设点P、Q运动时间为 $t (s)$ ．当 $△ P B Q$ 与 $△ A B C$ 相似时， $t$ 的值是多少？

查看试题解析