山东省德州市庆云县2022-2023学年九年级上学期期中数学试题

试卷更新日期：2022-12-20 类型：期中考试

进入出卷网下载

一、单选题

1. 下列美丽的图案，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若关于x的方程（m﹣1）x²+mx﹣1＝0是一元二次方程，则m的取值范围是（）

A、m≠1 B、m＝1 C、m≥1 D、m≠0

查看试题解析
3. 如图，AB为⊙O的弦，直径CD⊥AB，交AB于点H，连接OA，若∠A＝45°，AB＝2，则DH的长度为（　　）

A、1 B、 $\sqrt{2}$ ＋1 C、2 $\sqrt{2}$ －1 D、3

查看试题解析
4. 将二次函数 $y = 5 x^{2}$ 的图象向右平移2个单位，再向上平移3个单位得到该二次函数的表达式是（　　）

A、 $y = 5 {(x + 2)}^{2} + 3$ B、 $y = 5 {(x - 2)}^{2} - 3$ C、 $y = 5 {(x - 2)}^{2} + 3$ D、 $y = 5 {(x + 2)}^{2} + \frac{3}{5}$

查看试题解析
5. 设方程x²+x﹣2=0的两个根为α，β，那么（α﹣2）（β﹣2）的值等于（　　）

A、﹣4 B、0 C、4 D、2

查看试题解析
6. 如图，将一个含30°角的直角三角板 $A B C$ 绕点A旋转，使得点B，A， $C^{^{'}}$ 在同一条直线上，则旋转角的度数是（）

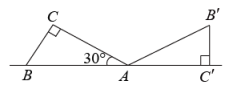A、30° B、60° C、120° D、150°

查看试题解析
7. 若关于x的一元二次方程kx²-2x-1＝0有两个实数根，则k的取值范围是（　　）

A、k≠0 B、k≥-1 C、k≥-1且k≠0 D、k＞-1且k≠0

查看试题解析
8. 如图，将 $R t △ A B C$ 绕点A按顺时针旋转一定角度得到 $R t △ A D E$ ，点B的对应点D恰好落在BC边上，若 $A B = 2 ， ∠ B = 60 °$ ，则CD的长为（）

A、1 B、 $\sqrt{3}$ C、2 D、 $2 \sqrt{2}$

查看试题解析
9. 二次函数 $y = - 2 x^{2} + b x + k$ 的图象如图所示，若 $(1 ， y_{1})$ ， $(- 2 ， y_{2})$ 、 $(- 1 ， y_{3})$ 在该函数的图象上，则 $y_{1}$ 、 $y_{2}$ 、 $y_{3}$ 的大小关系是（　　）

A、 $y_{2} > y_{1} > y_{3}$ B、 $y_{1} > y_{2} > y_{3}$ C、 $y_{1} > y_{3} > y_{2}$ D、 $y_{3} > y_{2} > y_{1}$

查看试题解析
10. 下列说法中，正确的个数为（　　）
⑴在同圆或等圆中，弦相等则所对的弧相等；
⑵优弧一定比劣弧长；
⑶弧相等则所对的圆心角相等；
⑷在同圆或等圆中，圆心角相等则所对的弦相等．

A、1个 B、2个 C、3个 D、4个

查看试题解析
11. 在某圆形喷水池的池中心竖直安装一根水管，在水管的顶端安一个喷水头，以水管与地面交点为原点，原点与水柱落地处所在直线为x轴，建立如图所示的平面直角坐标系，若喷出的抛物线形水柱解析式为 $y = - \frac{3}{4} {(x 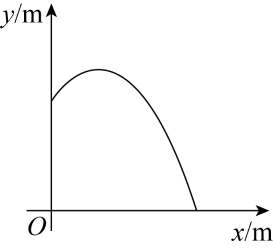- 1)}^{2} + 3$ （0≤x≤3），则水管长为（）

A、1m B、2m C、 $\frac{9}{4}$ m D、3m

查看试题解析
12. 如图，点A、B分别在x轴、y轴上（ $O A > O B$ ）；以 $A B$ 为直径的圆经过原点O，C是 $\overset{⌢}{A O B}$ 的中点，连结 $A C$ ， $B C$ ．下列结论：① $∠ A C B = 90 °$ ；② $A C = B C$ ；③若 $O A = 4$ ， $O B = 2$ ，则 $△ A B C$ 的面积等于5；④若 $O A - O B = 4$ ，则点C的坐标是 $(2 ， - 2)$ ，其中正确的结论有（　　）

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

13. $x = 1$ 是关于x的一元二次方程 $x^{2} + a x + 2 b = 0$ 的解，则 $a + 2 b =$ ．

查看试题解析
14. 若点A(4，n)与点B(－m，6)关于原点对称，则m＋n＝．

查看试题解析
15. 给出一种运算：对于函数 $y = x^{n}$ ，规定 $y^{'} = n x^{n - 1}$ ．例如：若函数 $y_{1} = x^{4}$ ，则有 ${y^{'}}_{1} = 4 x^{3}$ ．若函数 $y_{2} = x^{3}$ ，求方程 ${y^{'}}_{2} = 12$ 的解为．

查看试题解析
16. 已知：二次函数y=ax²+bx+c图像上部分点的横坐标x与纵坐标y的对应值如表格所示，那么它的图像与x轴的另一个交点坐标是．
x
…
-1
0
1
2
…
y
…
0
3
4
3
…

查看试题解析
17. 如图，在 $⊙ O$ 中，弦 $A B = 9$ ，点C在 $A B$ 上移动，连结 $O C$ ，过点C作 $C D ⊥ O C$ 交 $⊙ O$ 于点D，则 $C D$ 的最大值为．

查看试题解析
18. 在平面直角坐标系中，将如图所示的 $△ A B C$ 按照如下图所示的方式依次进行轴对称变换，若点A坐标是 $(x ， y)$ ，则经过第2022次变换后所得的点 $A_{2022}$ 坐标是．

查看试题解析

三、解答题

19. 解方程：

(1)、 $4 {(x - 1)}^{2} - 9 = 0$

(2)、 $x^{2} - 4 x - 2 = 0$

查看试题解析
20. 抛物线 $y = - x^{2} + 1$ 与x轴交于A、B两点（A在B的右侧），与y轴交于点C．

(1)、求线段 $A B$ 的长；

(2)、判断 $△ A B C$ 的形状．

查看试题解析
21. 如图，平面直角坐标系内，小正方形网格的边长为1个单位长度，△ABC的三个顶点的坐标分别为A（-1，3），B（-4，0），C．（0，0）
（ 1 ）将△ABC向上平移1个单位长度，再向右平移5个单位长度后得到的△A₁B₁C₁ ，画出△A₁B₁C₁ ，并直接写出点A₁的坐标；
（ 2 ）△ABC绕原点O逆时针方向旋转90°得到△A₂B₂O；
（ 3 ）如果△A₂B₂O，通过旋转可以得到△A₁B₁C₁ ，请直接写出旋转中心P的坐标

查看试题解析
22. 如图，某小区矩形绿地的长、宽分别为35m和15m，现计划对其进行扩充，将绿地的长宽增加相同的长度后，得到一个新的矩形绿地．

(1)、若扩充后的矩形绿地面积为 $800 m^{2}$ ，求新的矩形绿地长与宽．

(2)、若扩充后，实地测量发现新的矩形绿地的长宽之比为5：3，求新的矩形绿地面积．

查看试题解析
23. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，以 $B C$ 为直径作 $⊙ O$ ，交 $A B$ 边于点D，在 $\overset{⌢}{C D}$ 上取一点E，使 $\overset{⌢}{B E} = \overset{⌢}{C D}$ ，连接 $D E$ ，作射线 $C E$ 交 $A B$ 边于点F．

(1)、求证： $∠ A = ∠ A C F$ ；

(2)、若 $A C = 8$ ， $B C = 6$ ，求 $B F$ 的长．

查看试题解析
24. 阅读下列材料：
利用完全平方公式，可以将多项式 $a x^{2} + b x + c (a \neq 0)$ 变形为 $a (x + m)^{2} + n$ 的形式，我们把这样的变形方法叫做多项式 $a x^{2} + b x + c$ 的配方法．运用多项式的配方法及平方差公式能对一些多项式进行分解因式．

例如： $x^{2} + 11 x + 24$

＝ $x^{2} + 11 x + (\frac{11}{2})^{2} - (\frac{11}{2})^{2} + 24$

＝ $(x + \frac{11}{2})^{2} - \frac{25}{4}$

＝ $(x + \frac{11}{2} + \frac{5}{2}) (x + \frac{11}{2} - \frac{5}{2})$

＝ $(x + 8) (x + 3)$

根据以上材料，解答下列问题：

(1)、用多项式的配方法将 $x^{2} + 8 x - 1$ 化成 $(x + m)^{2} + n$ 的形式；

(2)、下面是某位同学用配方法及平方差公式把多项式 $x^{2} - 3 x - 40$ 进行分解因式的解答过程：

老师说，这位同学的解答过程中有错误，请你找出该同学解答中开始出现错误的地方，并用“ ”标画出来，然后写出完整的、正确的解答过程：

(3)、求证：x，y取任何实数时，多项式 $x^{2} + y^{2} - 2 x - 4 y + 16$ 的值总为正数．

查看试题解析
25. 如图，题目中的黑色部分是被墨水污染了无法辨认的文字，导致题目缺少了一个条件而无法解答，经查询结果发现，该二次函数解析式 $y = x^{2} - 4 x + 1$ ，

已知二次函数 $y = a x^{2} + b x + c$ 的图象经过点 $A (0 ， 1)$ ， $B (1 ， - 2)$ ，．

求该二次函数的解析式．

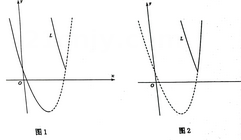(1)、请根据已有信息添加一个适当的条件：

(2)、当函数值 $y < 6$ ，自变量x的取值范围为：

(3)、如图1，将函数 $y = x^{2} - 4 x + 1 (x < 0)$ 的图象向右平移4个单位与 $y = x^{2} - 4 x + 1 (x \geq 4)$ 的图象组成一个新的函数图象，记为L，若点 $P (3 ， m)$ ，求m的值．

(4)、如图2，在（3）的条件下，点A的坐标为 $(2 ， 0)$ ，在L上是否存在点Q，使得 $S_{△ O A Q} = 9$ ，若存在，求出所有满足条件的点Q的坐标，不存在，说明理由．

查看试题解析

x	…	-1	0	1	2	…
y	…	0	3	4	3	…