山东省滨州市阳信县2022-2023学年九年级上学期期中数学试题

试卷更新日期：2022-12-20 类型：期中考试

进入出卷网下载

一、单选题

1. 下列说法正确的是（　　）

A、“打开电视机，正在播《都市报道60分》”是必然事件 B、“从一个装有6个红球的不透明的袋中摸出一个球是红球”是随机事件 C、“概率为0.0001的事件”是不可能事件 D、“经过有交通信号灯的路口，遇到红灯”是随机事件

查看试题解析
2. 下列关于圆的性质说法正确的是（）

A、平分弦的直径垂直于弦 B、三角形的内心是三条角平分线的交点 C、在同圆或等圆中，相等的弦所对的圆周角相等 D、三点确定一个圆

查看试题解析
3. 若将抛物线 $y = 5 x^{2}$ 先向右平移2个单位，再向上平移1个单位，得到的新抛物线的表达式为（）

A、 $y = 5 {(x - 2)}^{2} + 1$ B、 $y = 5 {(x + 2)}^{2} + 1$ C、 $y = 5 {(x - 2)}^{2} - 1$ D、 $y = 5 {(x + 2)}^{2} - 1$

查看试题解析
4. 如图，PA、PB是⊙O的切线，切点是A、B，已知∠P=60°，OA=3，那么∠AOB所对弧的长度为（）

A、6π B、5π C、3π D、2π

查看试题解析
5. 已知二次函数 $y = x^{2} - 2 x$ ，若点 $(- 1 ， y_{1})$ ， $(2 ， y_{2})$ 是它图象上的两点，则 $y_{1}$ 与 $y_{2}$ 的大小关系为（）

A、 $y_{1} > y_{2}$ B、 $y_{1} = y_{2}$ C、 $y_{1} < y_{2}$ D、不能确定

查看试题解析
6. 如图⊙O的直径 $A B$ 垂直于弦 $C D$ ，垂足是 $E$ ， $∠ A = 22.5 °$ ， $O C = 4$ ， $C D$ 的长为（）

A、 B、4 C、 D、8

查看试题解析
7. 如图，在△ABC中，AB=AC=5，BC=8，以A为圆心作一个半径为2的圆，下列结论中正确的是（　　）

A、点B在⊙A内 B、点C在⊙A上 C、直线BC与⊙A相切 D、直线BC与⊙A相离

查看试题解析
8. 二次函数 $y = (k + 1) x^{2} - 4 x + 1$ 的图象与x轴有两个交点，那么k的取值范围是（）

A、 $k \leq 3$ 且 $k \neq$ -1 B、 $k < 3$ 且 $k \neq$ -1 C、 $k \leq 3$ D、 $k < 3$

查看试题解析
9. 往直径为 $52 c m$ 的圆柱形容器内装入一些水以后，截面如图所示，若水面宽 $A B = 48 c m$ ，则水的最大深度为（）

A、 $8 c m$ B、 $10 c m$ C、 $16 c m$ D、 $20 c m$

查看试题解析
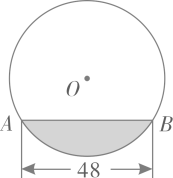10. 如图1，校运动会上，初一的同学们进行了投实心球比赛．我们发现，实心球在空中飞行的轨迹可以近似看作是抛物线．如图2建立平面直角坐标系，已知实心球运动的高度y（m）与水平距离x（m）之间的函数关系是y= $- \frac{1}{12} x^{2} + \frac{2}{3} x + \frac{5}{3}$ ，则该同学此次投掷实心球的成绩是（）

A、2m B、6m C、8m D、10m

查看试题解析
11. 如图，四边形ABCD内接于圆O，对角线AC是圆O的直径，DB平分 $∠ A B C$ ， AC长6cm，求阴影部分的面积（）

A、 $\frac{9}{4} π - \frac{9}{2}$ B、 $\frac{9}{4} π + \frac{9}{2}$ C、 $\frac{9}{4} π$ D、 $\frac{9}{4} π + \frac{9}{4}$

查看试题解析
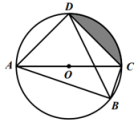12. 已知二次函数y＝ax²+bx+c的y与x的部分对应值如下表：

x

﹣2

﹣1

0

1

3

y

5

0

﹣3

﹣4

0

下列结论：①抛物线开口向上；②抛物线对称轴为直线x＝1；③ax²+bx+c＝5的另一个解是x＝4；④当﹣1＜x＜3时，y＞0；⑤抛物线与x轴的两个交点间的距离是4，其中，正确的个数（）

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

13. 为了估计鱼塘中的鱼数，养鱼者首先从鱼塘中打捞100条鱼，在每一条鱼身上做好记号后把这些鱼放归鱼塘，再从鱼塘中打捞10条鱼，如果在这10条鱼中有2条鱼是有记号的，那么估计鱼塘中鱼的条数为条．

查看试题解析
14. 如图，直线 $y = k x + b$ 与抛物线 $y = - x^{2} + 2 x + 3$ 交于A，B两点，其中点A（0，3），点B（3，0），抛物线与x轴的另一交点C（－1，0），不等式－x²+2x+3>kx+b的解集为

查看试题解析
15. 某一型号飞机着陆后滑行的距离y（单位：m）与滑行时间x（单位：s）之间的函数关系式是 $y = 80 x - 2 x^{2}$ ，该型号飞机着陆后滑行m才能停下来．

查看试题解析
16. 如图，四边形ABCD内接于⊙O，点M在AD的延长线上，∠AOC＝142°，则∠CDM＝.

查看试题解析
17. 如图，AB，AC，BD是⊙O的切线，P，C，D为切点，若AB=10，AC=7，则BD的长为．

查看试题解析
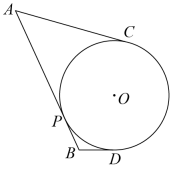18. 如图，在平面直角坐标系xOy中，P是直线y＝3上的一个动点，⊙P的半径为1，直线OQ切⊙P于点Q，则线段OQ的最小值为．

查看试题解析

三、解答题

19. 如图，用一段长为40m的篱笆围成一个一边靠墙的矩形花圃ABCD，墙长28m．设AB长为xm，矩形的面积为ym² ．

(1)、写出y与x的函数关系式；

(2)、当AB长为多少米时，所围成的花圃面积最大？最大值是多少？

查看试题解析
20. 有甲、乙两个不透明的布袋，甲袋中装有3个完全相同的小球，分别标有数字1，2，3；乙袋中装有3个完全相同的小球，分别标有数字 $- 1$ ， $- 2$ ， $- 3$ ．现从甲袋中随机摸出一个小球，将标有的数字记录为x，再从乙袋中随机摸出一个小球，将标有的数字记录为y，确定点M的坐标为 $(x ， y)$ ．

(1)、用树状图或列表法列举点M所有可能的坐标；

(2)、求点 $M (x ， y)$ 在一次函数 $y = - x - 1$ 的图像上的概率．

查看试题解析
21. 如图，AB是⊙O的直径，CD是⊙O的一条弦，且CD⊥AB于点E．

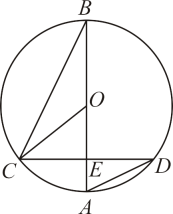(1)、求证：∠BCO＝∠D；

(2)、若BE＝8cm，CD＝6cm，求⊙O的半径．

查看试题解析
22. 某山区不仅有美丽风光，也有许多令人喜爱的土特产，为实现脱贫奔小康，山区组织村民加工包装土特产销售给游客，以增加村民收入．已知某种土特产每袋成本 $10$ 元，试销阶段每袋的销售价x（元）与该土特产的日销售量y（袋）之间的关系如表：
x（元）
$10$
$15$
$20$
…
y（袋）
$30$
$25$
$20$
…

(1)、若日销售量y（袋）是每袋的销售价x（元）的一次函数，求y与x之间的函数关系式．

(2)、假设后续销售情况与试销阶段效果相同，设每日销售土特产的利润为w（元）；
①求w与x之间的函数关系式；
②要使这种土特产每日销售的利润最大，每袋的销售价应定为多少元？每日销售的最大利润是多少元？

查看试题解析
23. 已知：如图， $A B$ 为 $⊙ O$ 的直径， $A B = A C$ ， $⊙ O$ 交 $B C$ 于 $D$ ， $D E ⊥ A C$ 于 $E$ ．

(1)、请判断 $D E$ 与 $⊙ O$ 的位置关系，并证明．

(2)、连接 $A D$ ，若 $⊙ O$ 的半径为2.5， $A D = 3$ ，求 $D E$ 的长．

查看试题解析
24. 如图，已知抛物线 $y = a x^{2} + b x + c$ 的顶点为A(4，3)，与y轴相交于点B(0，-5)，对称轴为直线l，点M是线段AB的中点．

(1)、求抛物线的表达式；

(2)、请求出点M的坐标及直线AB的表达式；

(3)、设动点P，Q分别在抛物线和对称轴l上，当以A，P，Q，M为顶点的四边形是平行四边形时，求P，Q两点的坐标．

查看试题解析

x	﹣2	﹣1	0	1	3
y	5	0	﹣3	﹣4	0

x（元）	$10$	$15$	$20$	…
y（袋）	$30$	$25$	$20$	…