河北省唐山市路南区2022-2023学年九年级上学期11月期中数学试题
试卷更新日期:2022-12-20 类型:期中考试
一、单选题
-
1. 若关于 的方程 有实数根,则 的取值范围是( )A、 B、 C、 D、2. 下列是有关北京2022年冬奥会的图片,其中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 已知是关于x的一元二次方程的一个根,则k的值为( )A、4 B、-4 C、±1 D、±44. 如图,将△ABC绕点C顺时针旋转90°得到△EDC.若∠ACB=20°,则∠ACD的度数是( )
3. 已知是关于x的一元二次方程的一个根,则k的值为( )A、4 B、-4 C、±1 D、±44. 如图,将△ABC绕点C顺时针旋转90°得到△EDC.若∠ACB=20°,则∠ACD的度数是( )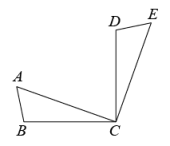 A、55° B、60° C、65° D、70°5. 如图,AB 是⊙O 的直径, ∠D=32° ,则∠AOC 等于( )
A、55° B、60° C、65° D、70°5. 如图,AB 是⊙O 的直径, ∠D=32° ,则∠AOC 等于( )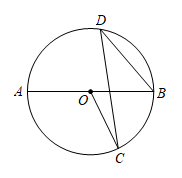 A、158° B、58° C、64° D、116°6. 根据4a=5b,可以组成的比例有( )A、a:b=4:5 B、a:b=5:4 C、a:4=b:5 D、a:5=4:b7. 已知a是方程的一个根,则代数式的值为( )A、1 B、 C、或1 D、28. 关于x的一元二次方程 有两个不相等的实数根,则m的值可能是( )A、8 B、9 C、10 D、119. 在平面直角坐标系中,点A(5,m)与点B(-5,-3)关于原点对称,则m的值为( )A、3 B、-3 C、5 D、-510. 已知和是一元二次方程的实数根,则的值为( )A、2 B、 C、1 D、11. 如图,已知的半径为6, , 是的弦,若 , 则的长是( )
A、158° B、58° C、64° D、116°6. 根据4a=5b,可以组成的比例有( )A、a:b=4:5 B、a:b=5:4 C、a:4=b:5 D、a:5=4:b7. 已知a是方程的一个根,则代数式的值为( )A、1 B、 C、或1 D、28. 关于x的一元二次方程 有两个不相等的实数根,则m的值可能是( )A、8 B、9 C、10 D、119. 在平面直角坐标系中,点A(5,m)与点B(-5,-3)关于原点对称,则m的值为( )A、3 B、-3 C、5 D、-510. 已知和是一元二次方程的实数根,则的值为( )A、2 B、 C、1 D、11. 如图,已知的半径为6, , 是的弦,若 , 则的长是( )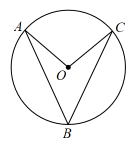 A、 B、10π C、 D、12π12. 如果在二次函数的表达式y=ax2+bx+c中,a>0,b<0,c<0,那么这个二次函数的图象可能是( )A、
A、 B、10π C、 D、12π12. 如果在二次函数的表达式y=ax2+bx+c中,a>0,b<0,c<0,那么这个二次函数的图象可能是( )A、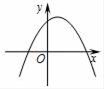 B、
B、 C、
C、 D、
D、 13. 如图, 、 、 是 的切线,切点分别为P、C、D,若 , ,则 的长是( )
13. 如图, 、 、 是 的切线,切点分别为P、C、D,若 , ,则 的长是( )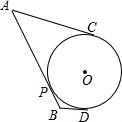 A、 B、 C、 D、14. 如图,中,已知 , , 点D在边上,线段绕着点逆时针旋转()后,如果点A恰好落在边上,那么的度数是( )
A、 B、 C、 D、14. 如图,中,已知 , , 点D在边上,线段绕着点逆时针旋转()后,如果点A恰好落在边上,那么的度数是( ) A、50° B、60° C、80° D、120°15. 已知抛物线的对称轴在轴右侧,现将该抛物线先向右平移3个单位长度,再向上平移1个单位长度后,得到的抛物线正好经过坐标原点,则的值是( )A、或2 B、 C、2 D、
A、50° B、60° C、80° D、120°15. 已知抛物线的对称轴在轴右侧,现将该抛物线先向右平移3个单位长度,再向上平移1个单位长度后,得到的抛物线正好经过坐标原点,则的值是( )A、或2 B、 C、2 D、二、填空题
-
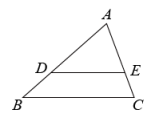
16. 函数的图象的开口向 .17. 若⊙O的直径是4,圆心O到直线l的距离为3,则直线l与⊙O的位置关系是 .18. 如图,已知点D、E在的边和上, , , , , 则 .
 19. 如图,在中, , , , 平分 , 点P为线段上一动点,以P为圆心,以1为半径长作圆,当与的边相切时,则长为 .
19. 如图,在中, , , , 平分 , 点P为线段上一动点,以P为圆心,以1为半径长作圆,当与的边相切时,则长为 .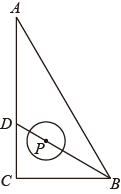
三、解答题
-
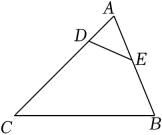
20. 解下列方程:(1)、(2)、21. 如图,分别是、上的点, , , , , , 求的长和的度数.
 22. 已知二次函数(1)、将二次函数的解析式化为的形式.(2)、写出二次函数图象的开口方向、对称轴、顶点坐标.23. 如图,以的边为直径作⊙O,交边于点D,为⊙O的切线,弦于点F,连接 .
22. 已知二次函数(1)、将二次函数的解析式化为的形式.(2)、写出二次函数图象的开口方向、对称轴、顶点坐标.23. 如图,以的边为直径作⊙O,交边于点D,为⊙O的切线,弦于点F,连接 .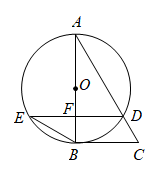 (1)、求证: .(2)、若点F为中点,且 , 求线段的长.24. 某小区计划用40米的篱笆围一个矩形花坛,其中一边靠墙 墙足够长,篱笆要全部用完 .
(1)、求证: .(2)、若点F为中点,且 , 求线段的长.24. 某小区计划用40米的篱笆围一个矩形花坛,其中一边靠墙 墙足够长,篱笆要全部用完 . (1)、如图1,问 为多少米时,矩形 的面积为200平方米?(2)、如图2,矩形 的面积比(1)中的矩形 面积减小20平方米,小明认为只要此时矩形的长 比图①中矩形的长 少2米就可以了.请你通过计算,判断小明的想法是否正确.25. 在平面直角坐标系中,二次函数的图象过点 , , 与x轴交于点A、B两点(点A在点B左侧).(1)、求该二次函数的解析式;(2)、在二次函数的图象上有一个点C,若满足 , 求C点的坐标.(3)、若一次函数的图象与二次函数的图象交点的横坐标分别为a和b,且 , 则一次函数恒过定点 , m的取值范围是 .
(1)、如图1,问 为多少米时,矩形 的面积为200平方米?(2)、如图2,矩形 的面积比(1)中的矩形 面积减小20平方米,小明认为只要此时矩形的长 比图①中矩形的长 少2米就可以了.请你通过计算,判断小明的想法是否正确.25. 在平面直角坐标系中,二次函数的图象过点 , , 与x轴交于点A、B两点(点A在点B左侧).(1)、求该二次函数的解析式;(2)、在二次函数的图象上有一个点C,若满足 , 求C点的坐标.(3)、若一次函数的图象与二次函数的图象交点的横坐标分别为a和b,且 , 则一次函数恒过定点 , m的取值范围是 .