河北省唐山市乐亭县2022-2023学年九年级上学期期中考试数学试题

试卷更新日期：2022-12-20 类型：期中考试

进入出卷网下载

一、单选题

1. 已知关于x的一元二次方程 $x^{2} + 3 x - m = 0$ 的一个根是 $x = 1$ ，则m的值为（）

A、2 B、4 C、-4 D、-2

查看试题解析
2. 根据4a=5b，可以组成的比例有（）

A、a：b=4：5 B、a：b=5：4 C、a：4=b：5 D、a：5=4：b

查看试题解析
3. 甲、乙、丙、丁四人进行射击测试，每人测试10次，平均成绩均为9.2环，方差如表所示．则在这四个选手中，成绩最稳定的是（）
选手
甲
乙
丙
丁
方差
$0.56$
$0.60$
$0.50$
$0.45$

A、甲 B、乙 C、丙 D、丁

查看试题解析
4. 如图，AB表示一条跳台滑雪赛道，在点A处测得起点B的仰角为35°，底端点C与顶端点B的距离为50米，则赛道AB的长度为（）米．

A、 $50 s i n 35 °$ B、 $50 c o s 35 °$ C、 $\frac{50}{s i n 35 °}$ D、 $\frac{50}{c o s 35 °}$

查看试题解析
5. 已知 $x = 0$ 是关于x的一元二次方程 $(m + 1) x^{2} + m x + 4 m^{2} - 4 = 0$ 的一个解，则m的值是（　　）

A、1 B、 $- 1$ C、0或1 D、1或 $- 1$

查看试题解析
6. 如图，一辆小车沿着坡度为 $i = 1 ： \sqrt{3}$ 的斜坡向上行驶了100米，则此时该小车上升的高度为（）

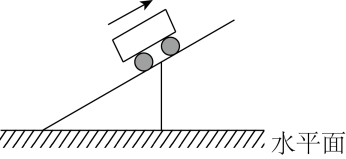A、50米 B、 $50 \sqrt{2}$ 米 C、 $50 \sqrt{3}$ 米 D、100米

查看试题解析
7. 一组数据：2，3，3，3，4，若去掉一个数据3，则下列统计量中发生变化的是（　　）

A、众数 B、中位数 C、平均数 D、方差

查看试题解析
8. 用配方法解一元二次方程 $2 x^{2} - 2 x - 1 = 0$ ，下列配方正确的是（）

A、 ${(x - \frac{1}{4})}^{2} = \frac{3}{4}$ B、 ${(x - \frac{1}{4})}^{2} = \frac{3}{2}$ C、 ${(x - \frac{1}{2})}^{2} = \frac{3}{4}$ D、 ${(x - \frac{1}{2})}^{2} = \frac{3}{2}$

查看试题解析
9. 如图， $△ A B C$ 与 $△ D E F$ 位似，位似中心为点O， $△ A B C$ 与 $△ D E F$ 的周长之比为 $4 ∶ 9$ ，则 $A O ∶ O D$ 的比为（　　）

A、2：3 B、2：5 C、4：9 D、4：13

查看试题解析
10. 如图所示，网格中相似的两个三角形是（）

A、①与② B、①与③ C、③与④ D、②与③

查看试题解析
11. 现有甲组数据：1、2、3、4、5，乙组数据：11、12、13、14、15；若甲、乙两组的方差分别为a、b，则a、b的关系是（）

A、 $a = b$ B、 $a = 10 + b$ C、 $a < b$ D、 $a > b$

查看试题解析
12. 如图在△ABC中，D、E分别是边AB、BC上的点，且DE $∥$ AC ，若S_△BDE：S_△CDE=2：3，则S_△DOE：S_△AOC的值为（）

A、 $\frac{2}{3}$ B、 $\frac{2}{5}$ C、 $\frac{4}{9}$ D、 $\frac{4}{25}$

查看试题解析
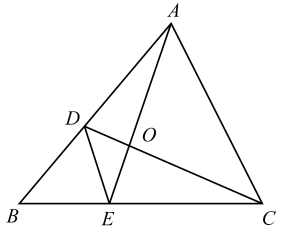13. 若a，b，c是△ABC的三边长，则关于x的方程 $x^{2} - (a + b) x + \frac{1}{4} c^{2} = 0$ 的根的情况是（　　）

A、无实数根 B、有两相等的实数根 C、有两不相等的实数根 D、无法确定

查看试题解析
14. 如图，△ABC，点D，点E分别在AC，AB上，连接DE，DE∥BC，过点B作BF∥AC交DE的延长线于点F，则下列结论错误的是（）

A、 $\frac{A D}{A C} = \frac{A E}{A B}$ B、 $\frac{A D}{C D} = \frac{E F}{D E}$ C、 $\frac{B E}{A E} = \frac{C D}{A D}$ D、 $\frac{B E}{A B} = \frac{F E}{C B}$

查看试题解析
15. 已知关于x的一元二次方程 $x^{2} - (m + 3) x + 3 m = 0$ ，若等腰三角形的其中一边为4，另两边是这个方程的两根，则m的值为（　　）

A、3 B、4 C、3或4 D、不能确定

查看试题解析
16. 如图， $O$ 为正方形 $A B C D$ 对角线 $A C$ 上一动点， $O E ⊥ O D$ ， $∠ O D E = 45 °$ ， $E$ 在 $A B$ 上结论：① $O D = O E$ ；② $∠ A D E = ∠ A O E$ ；③ $D G^{2} = G O \cdot G C$ ；④若 $A B = 3$ ， $A E = 1$ ，则 $O E = \sqrt{5}$ ．其中正确结论的个数是（）

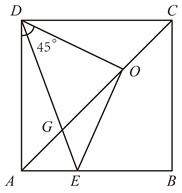A、1 B、2 C、3 D、4

查看试题解析

二、填空题

17. 如果线段a＝4厘米，c＝9厘米，那么线段a、c的比例中项b＝厘米．

查看试题解析
18. 在 $△ A B C$ 中，若 $| s i n A - \frac{\sqrt{3}}{2} | + {(t a n B - 1)}^{2} = 0$ ，则 $∠ C$ 的度数为

查看试题解析
19. 小聪同学在计算一组数据1、3、4、5、x的方差时，写出的计算过程是： $S^{2} = \frac{1}{5} [(1 - 4)^{2} + (3 - 4)^{2} + (4 - 4)^{2} + (5 - 4)^{2} + (x - 4)^{2}] = 4$ ，如果他的计算是正确的，你认为这组数据中的x为．

查看试题解析
20. 如图，用120米长的围网围建一个面积为560平方米的矩形养殖场．为了节省材料，养殖场的一边靠墙（墙足够长），并在如图的两个位置各开出一个1米宽的门（门不用围网做）．设矩形AB边长为x米，请依题意列方程：．

查看试题解析

三、解答题

21. 已知关于x的一元二次方程 $m x^{2} + (2 m - 1) x + m - 4 = 0$ ．

(1)、当m为何值时，方程有两个不相等的实数根？

(2)、当 $m = 2$ 时，用合适的方法求此时该方程的解．

查看试题解析
22. 在一次大学生一年级新生训练射击训练中，某小组的成绩如表：
环数
6
7
8
9
人数
1
5
3
1

(1)、该小组射击数据的众数是，中位数是；

(2)、求该小组的平均成绩；

(3)、若8环（含8环）以上为优秀射手，在1200名新生中有多少人可以评为优秀射手？

查看试题解析
23. 如图，小明在大楼30米高（即PH＝30米）的窗口P处进行观测，测得山坡上A处的俯角∠APQ为15°，山脚B处的俯角∠BPQ为60°，已知该山坡的坡度i（即tan∠ABC）为1： $\sqrt{3}$ ，点P，H，B，C，A在同一个平面上，点H、B、C在同一条直线上，且PH丄HC.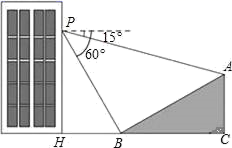

(1)、求出山坡坡角（∠ABC）的大小；

(2)、求A、B两点间的距离（结果精确到0.1米，参考数据： $\sqrt{3}$ ≈1.732）.

查看试题解析
24. 如图，在等边三角形 $A B C$ 中， $A B = 4$ ， P是边 $A B$ 上一点， $B P = \frac{3}{2}$ ， D是边 $B C$ 上一点（点D不与端点重合），作 $∠ P D Q = 60 °$ ， $D Q$ 交边 $A C$ 于点Q．

(1)、 $△ B D P ∽ △ C Q D$

(2)、若 $C Q = a$ ，满足条件的点D有且只有一个，求a的值．

查看试题解析
25. 某大型电子商场销售某种空调，每台进货价为 $2500$ 元，标价为 $3200$ 元．

(1)、若电子商场连续两次降价，每次降价的百分率相同，最后以 $2592$ 元售出，求每次降价的百分率；

(2)、市场调研表明：当每台售价为 $3000$ 元时，平均每天能售出 $10$ 台，当每台售价每降 $100$ 元时，平均每天就能多售出4台，若商场要想使这种空调的销售利润平均每天达到 $5400$ 元，且顾客得到优惠，则每台空调应降价多少元？

查看试题解析
26. 如图所示，E是矩形ABCD的边BC上一点，EF⊥AE，分别交AC，CD于点M，F，BG⊥AC，垂足为G，BG交AE于点H．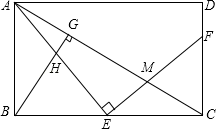

(1)、求证：△ABE∽△ECF；

(2)、找出与△ABH相似的三角形，并证明；

(3)、若E是BC中点，BC=2AB，AB=4，求EM的长．

查看试题解析

选手	甲	乙	丙	丁
方差	$0.56$	$0.60$	$0.50$	$0.45$

环数	6	7	8	9
人数	1	5	3	1