山东省淄博市周村区2022-2023学年七年级上学期期中数学试题
试卷更新日期:2022-12-20 类型:期中考试
一、单选题
-
1. 如果一个三角形是轴对称图形,那么这个三角形一定是( )A、直角三角形 B、等腰直角三角形 C、等边三角形 D、等腰三角形2. 如图所示在 中, 边上的高线画法正确的是( )A、
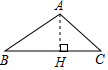 B、
B、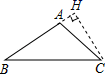 C、
C、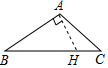 D、
D、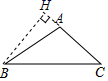 3. 以下列各组线段为边,能组成三角形的是( )
3. 以下列各组线段为边,能组成三角形的是( )
A、1cm,2cm,4cm B、4cm,6cm,8cm C、5cm,6cm,12cm D、2cm,3cm,5cm4. 如图,在 中, , , 平分 ,则 的度数是( )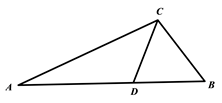 A、 B、 C、 D、5. 如图,在 中 , 是 的中点, ,则 ( ).
A、 B、 C、 D、5. 如图,在 中 , 是 的中点, ,则 ( ). A、108° B、72° C、54° D、36°6. 如图,点E,点F在直线AC上,AF=CE,AD=CB,下列条件中不能推断 ADF≌ CBE的是( )
A、108° B、72° C、54° D、36°6. 如图,点E,点F在直线AC上,AF=CE,AD=CB,下列条件中不能推断 ADF≌ CBE的是( ) A、∠D=∠B B、∠A=∠C C、BE=DF D、AD∥BC7. 如图,在中,是边上的高,点E,F是上的两点, , , , 则图中阴影部分的面积是( )
A、∠D=∠B B、∠A=∠C C、BE=DF D、AD∥BC7. 如图,在中,是边上的高,点E,F是上的两点, , , , 则图中阴影部分的面积是( ) A、12 B、6 C、3 D、48. 如图, ,过点A作 ,垂足为点F , 若 ,则 的度数为( )
A、12 B、6 C、3 D、48. 如图, ,过点A作 ,垂足为点F , 若 ,则 的度数为( )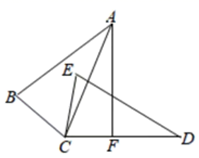 A、15° B、25° C、35° D、65°9. 如图,AD,BE是△ABC的高线,AD与BE相交于点F.若AD=BD=6,且△ACD的面积为12,则AF的长度为( )
A、15° B、25° C、35° D、65°9. 如图,AD,BE是△ABC的高线,AD与BE相交于点F.若AD=BD=6,且△ACD的面积为12,则AF的长度为( ) A、4 B、3 C、2 D、1.510. 剪纸是我国传统的民间艺术.如图①,②将一张纸片进行两次对折后,再沿图③中的虚线裁剪,最后将图④中的纸片打开铺平,所得图案应该是( )
A、4 B、3 C、2 D、1.510. 剪纸是我国传统的民间艺术.如图①,②将一张纸片进行两次对折后,再沿图③中的虚线裁剪,最后将图④中的纸片打开铺平,所得图案应该是( )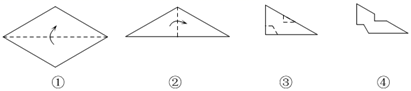 A、
A、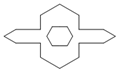 B、
B、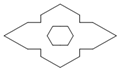 C、
C、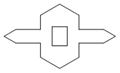 D、
D、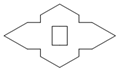 11. 如图,在中, , M,N,P分别是边AB,AC,BC上的点,且 , , 若 , 则的度数为( )
11. 如图,在中, , M,N,P分别是边AB,AC,BC上的点,且 , , 若 , 则的度数为( ) A、 B、 C、 D、12. 如图,将三角形纸片沿折叠,使点C落在边上的点E处.若 , , 则的值为( )
A、 B、 C、 D、12. 如图,将三角形纸片沿折叠,使点C落在边上的点E处.若 , , 则的值为( ) A、16 B、18 C、20 D、24
A、16 B、18 C、20 D、24二、填空题
-
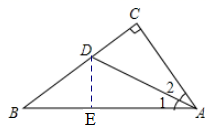
13. 若等腰三角形的一个内角为92°,则它的顶角的度数为 °.14. 如图, , ,若 , ,则D到AB的距离为。
 15. 如图,在中, , , 垂直平分交于点E, , 则 .
15. 如图,在中, , , 垂直平分交于点E, , 则 . 16. 一块钢板的形状如图所示,已知AB=12cm,BC=13cm,CD=4cm,AD=3cm,∠ADC=90°,则这块钢板的面积是 cm2 .
16. 一块钢板的形状如图所示,已知AB=12cm,BC=13cm,CD=4cm,AD=3cm,∠ADC=90°,则这块钢板的面积是 cm2 . 17. 如图,在中,已知 , , , 平分 . 若分别是和上的动点,则的最小值是 .
17. 如图,在中,已知 , , , 平分 . 若分别是和上的动点,则的最小值是 .
三、解答题
-
18. 如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°.
 (1)、求∠DAC的度数;(2)、求证:DC=AB.19. 如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫格点,网格中有以格点A、B、C为顶点的 , 请你根据所学的知识回答下列问题:
(1)、求∠DAC的度数;(2)、求证:DC=AB.19. 如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫格点,网格中有以格点A、B、C为顶点的 , 请你根据所学的知识回答下列问题: (1)、判断的形状,并说明理由:(2)、求的面积.20. 如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)、判断的形状,并说明理由:(2)、求的面积.20. 如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.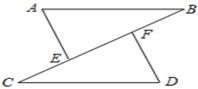 (1)、求证:AB=CD;(2)、若AB=CF,∠B=40°,求∠D的度数.21. 如图, , , 的垂直平分线交于点D.
(1)、求证:AB=CD;(2)、若AB=CF,∠B=40°,求∠D的度数.21. 如图, , , 的垂直平分线交于点D. (1)、求的度数;(2)、求证: .22. 如图,在等腰△ABC中,AB=AC,BC=5.点D为AC上一点,且BD=4,CD=3.
(1)、求的度数;(2)、求证: .22. 如图,在等腰△ABC中,AB=AC,BC=5.点D为AC上一点,且BD=4,CD=3. (1)、求证:BD⊥AC;(2)、求AB的长.23. 如图,在正方形网格中,每个小正方形的边长均相等,的三个顶点A,B,C都在格点上.
(1)、求证:BD⊥AC;(2)、求AB的长.23. 如图,在正方形网格中,每个小正方形的边长均相等,的三个顶点A,B,C都在格点上. (1)、在图中画出与关于直线l成轴对称的;(2)、在直线l上找出一点Q,使得的值最小;(描出该点并标注字母Q)(3)、在直线l上找出一点P,使得的值最大.(保留作图痕迹并标注点P)24. 在△ABC中,AB=AC,点D是射线CB上的一动点(不与点B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)、在图中画出与关于直线l成轴对称的;(2)、在直线l上找出一点Q,使得的值最小;(描出该点并标注字母Q)(3)、在直线l上找出一点P,使得的值最大.(保留作图痕迹并标注点P)24. 在△ABC中,AB=AC,点D是射线CB上的一动点(不与点B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE. (1)、如图1,当点D在线段CB上,且∠BAC=90°时,判断BD和CE的数量关系和位置关系,并说明理由;(2)、设∠BAC= , ∠DCE= . 如图2,当点D在线段CB上,∠BAC≠90°时,请你探究与之间的数量关系,并证明你的结论;
(1)、如图1,当点D在线段CB上,且∠BAC=90°时,判断BD和CE的数量关系和位置关系,并说明理由;(2)、设∠BAC= , ∠DCE= . 如图2,当点D在线段CB上,∠BAC≠90°时,请你探究与之间的数量关系,并证明你的结论;