山东省烟台市牟平区2022-2023学年七年级上学期期中数学试题
试卷更新日期:2022-12-20 类型:期中考试
一、单选题
-
1. 下列说法正确的是( )A、有一角和两边对应相等的两个三角形全等 B、三角形的任意两边之和大于第三边 C、线段不是轴对称图形 D、三角形的重心是这个三角形的三条角平分线的交点2. 山东省第二十五届运动会于2022年8月25日开幕,“全民健身与省运同行”成为我省体育运动的主题.在下列给出的运动图片中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图,在 中, 是 的角平分线,过点D分别作 ,垂足分别是点E,F,则下列结论错误的是( )
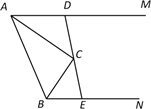
3. 如图,在 中, 是 的角平分线,过点D分别作 ,垂足分别是点E,F,则下列结论错误的是( )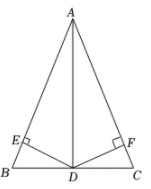 A、 B、 C、 D、4. 如图,直线l1l2 , 点C、A分别在l1、l2上,以点C为圆心,CA长为半径画弧,交l1于点B,连接AB.若∠BCA=150°,则∠1的度数为( )
A、 B、 C、 D、4. 如图,直线l1l2 , 点C、A分别在l1、l2上,以点C为圆心,CA长为半径画弧,交l1于点B,连接AB.若∠BCA=150°,则∠1的度数为( ) A、10° B、15° C、20° D、30°5. 两根木条的长分别是4cm和9cm,要拼成一个三角形,若第三根木条的长度为奇数,则第三根木条的长度的取值情况有( )A、3种 B、4种 C、5种 D、0种6. 等腰三角形的一个角是 , 则它的一个底角是( )A、 B、 C、或 D、或7. 在中, , 且 , 则的最长的边的长度是( )A、4 B、6 C、8 D、98. 如图,直四棱柱,底面是边长为的正方形,侧棱长为 , 点是的中点,蚂蚁从点沿着表面爬行到点的最短路程是 , 则的值是( )
A、10° B、15° C、20° D、30°5. 两根木条的长分别是4cm和9cm,要拼成一个三角形,若第三根木条的长度为奇数,则第三根木条的长度的取值情况有( )A、3种 B、4种 C、5种 D、0种6. 等腰三角形的一个角是 , 则它的一个底角是( )A、 B、 C、或 D、或7. 在中, , 且 , 则的最长的边的长度是( )A、4 B、6 C、8 D、98. 如图,直四棱柱,底面是边长为的正方形,侧棱长为 , 点是的中点,蚂蚁从点沿着表面爬行到点的最短路程是 , 则的值是( ) A、20 B、148 C、400 D、4649. 如图,在中, , , 点D是上一点,将沿折叠,使点B落在边上处,则的度数为( )
A、20 B、148 C、400 D、4649. 如图,在中, , , 点D是上一点,将沿折叠,使点B落在边上处,则的度数为( )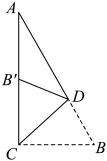 A、 B、 C、 D、10. 在学习三角形时,李峰同学发现可以折叠出三角形的高. 他在折叠其中一个三角形纸片时,只能折叠出一条高,这个纸片的形状是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、直角三角形或钝角三角形11. 在△ABC和△A1B1C1中,已知∠C=∠A1 , ∠B=∠B1 , 要使这两个三角形全等,还需要条件( )A、AB=A1B1 B、AB=A1C1 C、CA=A1C1 D、∠A=∠C112. 如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC , AD=AE , 点C , D , E在同一条直线上,连接B , D和B , E . 下列四个结论:
A、 B、 C、 D、10. 在学习三角形时,李峰同学发现可以折叠出三角形的高. 他在折叠其中一个三角形纸片时,只能折叠出一条高,这个纸片的形状是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、直角三角形或钝角三角形11. 在△ABC和△A1B1C1中,已知∠C=∠A1 , ∠B=∠B1 , 要使这两个三角形全等,还需要条件( )A、AB=A1B1 B、AB=A1C1 C、CA=A1C1 D、∠A=∠C112. 如图,在△ABC和△ADE中,∠BAC=∠DAE=90°,AB=AC , AD=AE , 点C , D , E在同一条直线上,连接B , D和B , E . 下列四个结论: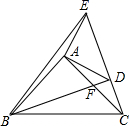
①BD=CE , ②BD⊥CE , ③∠ACE+∠DBC=30°,④ .其中,正确的个数是( )
A、1 B、2 C、3 D、4二、填空题
-
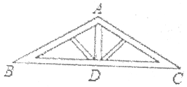
13. 写出一个有3条对称轴的平面图形 .14. 如图,屋顶钢架外框是等腰三角形,其中 , 立柱 , 且顶角 , 立柱 , 则的值为 .
 15.
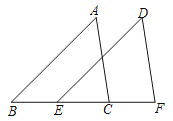
15.如图,点B、E、C、F在一条直线上,AB∥DE,且AB=DE,请添加一个条件 , 使△ABC≌△DEF.
 16. 如图,牧童在A处放牛,牛棚在B处,A、B到河岸的距离相等,即 , 若点A到河岸的距离为 , C、D两点间的距离为 , 则牧童从A处把牛牵到河边饮完水,再把牛送回牛棚的最短路程是 .
16. 如图,牧童在A处放牛,牛棚在B处,A、B到河岸的距离相等,即 , 若点A到河岸的距离为 , C、D两点间的距离为 , 则牧童从A处把牛牵到河边饮完水,再把牛送回牛棚的最短路程是 .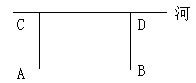 17. 如图,在 网格中,各小正方形边长均为1,点O,A,B,C,D,E均在格点上,点O是 的外心,在不添加其他字母的情况下,则除 外把你认为外心也是O的三角形都写出来 .
17. 如图,在 网格中,各小正方形边长均为1,点O,A,B,C,D,E均在格点上,点O是 的外心,在不添加其他字母的情况下,则除 外把你认为外心也是O的三角形都写出来 .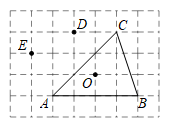 18. 下列说法:
18. 下列说法:①因为0.6,0.8,1不是勾股数,所以以0.6,0.8,1为边的三角形不是直角三角形
②若a,b,c是勾股数,且 , , 则必有
③因以0.5,1.2,1.3为边长的三角形是直角三角形,所以0.5,1.2,1.3是勾股数
④若三个整数a,b,c是直角三角形的三条边,则3a,3b,3c必是勾股数
其中正确的是(填序号).
三、解答题
-
19. 已知: , .
求作:点 , 使点在内部.且 , .
 20. 如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A、B间的距离,但绳子不够长,你能帮他想个办法吗?
20. 如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A、B间的距离,但绳子不够长,你能帮他想个办法吗? (1)、把你的方法写出来.(2)、写出其中的道理.21. 如图, ,AD是 内部一条射线,若 , 于点E, 于点F.求证: .
(1)、把你的方法写出来.(2)、写出其中的道理.21. 如图, ,AD是 内部一条射线,若 , 于点E, 于点F.求证: . 22. 问题情境:
22. 问题情境:在数学探究活动中,老师给出了如图的图形及下面三个等式:;; . 若以其中两个等式作为已知条件,能否得到余下一个等式成立?
解决方案:
探究与全等.
问题解决:
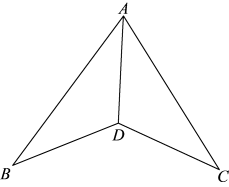 (1)、当选择①②作为已知条件时,与全等吗? ▲ (填“全等”或“不全等”),为什么?(2)、任意选择两个等式作为已知条件,可以说明的还有 .(3)、选择这两个条件不能说明 , 再加上这个条件就可以说明 .23. 如图所示,有一个直角三角形纸片,两直角边 , , 现将直角边AC沿直线AD折叠,使它落在斜边AB上且与AE重合,求CD的长.
(1)、当选择①②作为已知条件时,与全等吗? ▲ (填“全等”或“不全等”),为什么?(2)、任意选择两个等式作为已知条件,可以说明的还有 .(3)、选择这两个条件不能说明 , 再加上这个条件就可以说明 .23. 如图所示,有一个直角三角形纸片,两直角边 , , 现将直角边AC沿直线AD折叠,使它落在斜边AB上且与AE重合,求CD的长. 24. 如图,在10×10的正方形网格中,小正方形的顶点称为格点,顶点均在格点上的图形称为格点图形,图中为格点三角形.请按要求作图,不需说明.
24. 如图,在10×10的正方形网格中,小正方形的顶点称为格点,顶点均在格点上的图形称为格点图形,图中为格点三角形.请按要求作图,不需说明. (1)、在图1中,作出三个与全等的格点三角形,要求所作格点三角形与有一条公共边,且不与重叠;(2)、在图2中,作出关于直线l对称的三角形 .
(1)、在图1中,作出三个与全等的格点三角形,要求所作格点三角形与有一条公共边,且不与重叠;(2)、在图2中,作出关于直线l对称的三角形 .