山东省潍坊市奎文区2022-2023学年七年级上学期期中数学试题

试卷更新日期：2022-12-20 类型：期中考试

进入出卷网下载

一、单选题

1. -4的倒数为（）

A、 $- 4$ B、 $- \frac{1}{4}$ C、4 D、 $\frac{1}{4}$

查看试题解析
2. 中国古代数学著作《九章算术》第八章（《方程》篇）中最早使用了负数．如果支出160元记作 $- 160$ 元，那么 $+ 60$ 元表示（）

A、收入60元 B、支出60元 C、收入100元 D、支出100元

查看试题解析
3. 下列几何图形与相应语言描述相符的是（）

A、如图1所示，延长线段 $B A$ 到点 $C$ B、如图2所示，射线 $C B$ 不经过点 $A$ C、如图3所示，直线 $a$ 和直线 $b$ 相交于点 $A$ D、如图4所示，射线 $C D$ 和线段 $A B$ 没有交点

查看试题解析
4. 下列调查方式合适的是（）

A、为了解市民对电影《平凡英雄》的感受，小明在某校随机采访了8名初三学生 B、为了解全校学生国庆节假期做实践作业的时间，小莹同学在网上向3位好友做了调查 C、为了解全国青少年儿童的睡眠时间，统计人员采用了普查的方式 D、为了解“神舟十四号”载人飞船发射前零部件的状况，检测人员采用了普查的方式

查看试题解析
5. 如图是一个正方体的表面展开图，则原正方体与“祖”所在面相对的面上的汉字是（）

A、我 B、和 C、国 D、的

查看试题解析
6. 国家疾控中心网站显示：截至2022年9月28日，全国累计报告接种新冠疫苗34亿3663万剂次，覆盖人数13亿323.2万元，其中数据3663万用科学记数法（精确到百万位）表示为（）

A、 $3.663 \times 1 0^{7}$ B、 $0.36 \times 1 0^{8}$ C、 $3.7 \times 1 0^{7}$ D、 $3.7 \times 1 0^{8}$

查看试题解析
7. 与下面科学计算器的按键顺序对应的计算任务是（）

A、 $- 1 5^{4} \div 5 \times 2$ B、 $- 1 5^{4} \div 5^{2}$ C、 ${(- 15)}^{4} \div 5 \times 2$ D、 ${(- 15)}^{4} \div 5^{2}$

查看试题解析
8. 如图，数轴上 $A$ ， $B$ 两点所表示的有理数分别是 $a$ ， $b$ ，则下列结论正确的是（）

A、 $a > - b$ B、 $| a | > | b |$ C、 $(a - 1) (b + 1) > 0$ D、 $| a + b | = | a | + | b |$

查看试题解析

二、多选题

9. 下列各组数中，相等的是（）

A、 $\frac{2^{2}}{3}$ 与 ${(\frac{2}{3})}^{2}$ B、 ${(- 4)}^{3}$ 与 $- 4^{3}$ C、 ${| - 5 |}^{3}$ 与 $- {(- 5)}^{3}$ D、 $- 3^{4}$ 与 ${(- 3)}^{4}$

查看试题解析
10. 如图，两根木条的长度分别为 $7 c m$ 和 $12 c m$ ，在它们的中点处各打一个小孔 $M$ ， $N$ （木条的厚度，宽度及小孔大小均忽略不计）．将这两根木条的一端重合并放置在同一条直线上，则两小孔间的距离 $M N$ 为（）

A、 $19 c m$ B、 $9.5 c m$ C、 $5 c m$ D、 $2.5 c m$

查看试题解析
11. 随着物联网技术的推广与应用，我国快递行业得到迅猛发展．结合下图所提供的信息，请你判断以下结论正确的是（）

A、2017-2021年，快递业务量持续增加 B、2017-2021年，快递业务量较上一年的增长速度持续提高 C、2017-2021年，较上一年快递业务量的增长速度最快的是2020年 D、2021年较2017年快递业务量的增长速度是57.9%

查看试题解析
12. 下表为国外几个城市与北京的时差（正数表示同一时刻比北京时间早的时数）
城市
东京
伦敦
巴黎
莫斯科
纽约
悉尼
时差/时
$+ 1$
$- 8$
$- 7$
$- 5$
$- 13$
$+ 2$
则以下说法正确的是（）

A、北京10月7日23时，悉尼10月8日1时 B、伦敦10月7日23时，巴黎10月7日22时 C、东京时间比悉尼时间早一个小时 D、10月7日23时从北京出发，经16小时到达纽约，此时纽约时间为10月8日2时

查看试题解析

三、填空题

13. 计算： $- 1^{6} \div \frac{1}{3} =$ ．

查看试题解析
14. 如图，小亮将一个衣架固定在墙上，他在衣架两端各用一个钉子进行固定，请你用数字知识解释他这样操作的原因是．

查看试题解析
15. 若 $a$ 和 $b$ 互为相反数， $m$ 是最大的负整数，则 $a + b - m =$ ．

查看试题解析
16. 如图，下面的几何体是由图（填写序号）的平面图形绕直线 $l$ 旋转一周得到的．

查看试题解析
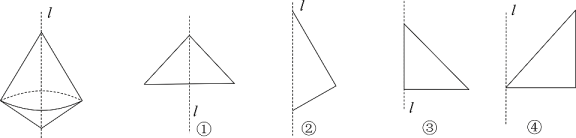17. 在数轴上，点 $A$ 到2的距离为3，则点 $A$ 到原点的距离为．

查看试题解析
18. 已知有理数x，y，数 $| x | = 3$ ， $| y | = 2$ ，且 $x < 0 < y$ ，则 $x^{y} =$ ．

查看试题解析
19. 观察下列各式： $- 1 \times \frac{1}{2} = - 1 + \frac{1}{2}$ ， $- \frac{1}{2} \times \frac{1}{3} = - \frac{1}{2} + \frac{1}{3}$ ， $- \frac{1}{3} \times \frac{1}{4} = - \frac{1}{3} + \frac{1}{4}$ ， …
试运用你发现的规律计算：
$(- 1 \times \frac{1}{2}) + (- \frac{1}{2} \times \frac{1}{3}) + (- \frac{1}{3} \times \frac{1}{4}) + \cdot \cdot \cdot + (- \frac{1}{2020} \times \frac{1}{2021}) + (- \frac{1}{2021} \times \frac{1}{2022}) =$ ．

查看试题解析

四、解答题

20. 计算下列各题：

(1)、 $- 8 - (- 12) + (- 16) + 11$ ；

(2)、 $- 0.9 + \frac{2}{5} - 8.1 - \frac{7}{5}$ ；

(3)、 $(\frac{1}{2} - \frac{2}{3} - \frac{5}{6}) \div (- \frac{1}{36})$ ；

(4)、 $32 \times {(- \frac{1}{2})}^{3} - 0 . 5^{2} \times | - 2^{3} |$ ．

查看试题解析
21. 画一条数轴，在数轴上表示下列各数，并把它们按照从小到大的顺序用“＜”号连接起来．
$- 1$ ， $- (- 2)$ ， 0， $- 2.5$ ， $| - 5 |$ ， $3 \frac{1}{2}$

查看试题解析
22. 某校利用“阳光大课间”开展跳绳训练活动以增强学生体质．为检测训练效果，学期初和学期末体育老师对七年级的200名学生分别进行“30秒跳绳数量”的摸底测试和终结测试，将两次测试数据绘制成如图的统计表和扇形统计图．
“30秒跳绳数量”测试成绩的人数统计表
跳绳个数（ $x$ ）
$x \leq 50$
$50 < x \leq 60$
$60 < x \leq 70$
$70 < x \leq 80$
$x > 80$
人数（摸底测试）
19
27
$a$
65
17
人数（终结测试）
3
6
59
$b$
$c$
请按要求回答下列问题：

(1)、表格中 $a =$ ； $b =$ ； $c =$ ．

(2)、请计算“ $x > 80$ ”对应的扇形圆心角的度数；

(3)、若“30秒跳绳”数量超过80个为优秀，请问经过一个学期的训练，该校七年级学生“30秒跳绳”的优秀率提高了多少？

查看试题解析
23. 已知点 $C$ 在直线 $A B$ 上，点 $M$ ， $N$ 分别为 $A C$ ， $B C$ 的中点．

(1)、如图所示，若 $C$ 在线段 $A B$ 上， $A C = 6$ 厘米， $M B = 10$ 厘米，求线段 $B C$ ， $M N$ 的长；

(2)、若点 $C$ 在线段 $A B$ 的延长线上，且满足 $A C - B C = a$ 厘米，请根据题意画图，并求 $M N$ 的长度（结果用含 $a$ 的式子表示）．

查看试题解析
24. 某风筝加工厂计划一周生产某种型号的风筝700只，平均每天生产100只，但由于种种原因，实际每天生产量与计划量相比有出入．下表是某周的生产情况（增产记为正、减产记为负）；
星期
一
二
三
四
五
六
日
增减
$+ 5$
$- 2$
$- 4$
$+ 13$
$- 6$
$+ 6$
$- 3$

(1)、根据记录的数据，该厂生产风筝最多的一天是星期；

(2)、产量最多的一天比产量最少的一天多生产多少只风筝？

(3)、该厂实行每周计件工资制，每生产一只风筝可得20元，若超额完成任务，则超过部分每只另奖5元；少生产一只扣4元，那么该厂工人这一周的工资总额是多少元？

查看试题解析
25. 如图，在一张纸面上画了一条数轴，数轴上从左到右有点 $A$ ， $B$ ， $C$ ， $D$ ，其中点 $C$ 为原点， $A$ ， $D$ 所对应的数分别为 $- 5$ ， 1，点 $B$ 为 $A D$ 的中点．

(1)、请在图中标出点B，C的位置；

(2)、已知数轴上有两点 $P$ 和 $Q$ ，点 $P$ 在点 $Q$ 的左侧，且 $P Q = 10$ ，折叠一次纸面，使点 $A$ 与点 $D$ 重合，若此时点 $P$ 和 $Q$ 也恰好重合，则点 $P$ 表示的数是 ▲ ，点Q表示的数是 ▲ ；请在图中标出点P和Q的位置；

(3)、已知点M是数轴上的一动点．
①当点M分别到（2）中P，Q两点的距离之和是16时，请求出点M表示的数；
②请直接写出点M在数轴上何位置时，它到P，A，D，Q四点的距离之和最小．

查看试题解析

城市	东京	伦敦	巴黎	莫斯科	纽约	悉尼
时差/时	$+ 1$	$- 8$	$- 7$	$- 5$	$- 13$	$+ 2$

跳绳个数（ $x$ ）	$x \leq 50$	$50 < x \leq 60$	$60 < x \leq 70$	$70 < x \leq 80$	$x > 80$
人数（摸底测试）	19	27	$a$	65	17
人数（终结测试）	3	6	59	$b$	$c$

星期	一	二	三	四	五	六	日
增减	$+ 5$	$- 2$	$- 4$	$+ 13$	$- 6$	$+ 6$	$- 3$