山东省青岛市李沧区2022-2023学年七年级上学期期中数学试题
试卷更新日期:2022-12-20 类型:期中考试
一、单选题
-
1. 2023的相反数是( )A、 B、2023 C、 D、2. 中国人最先使用负数,魏晋时期的数学家刘徽在“正负术”的注文中指出,可将算筹(小棍形状的记数工具)正放表示正数,斜放表示负数.根据刘徽的这种表示法,图1表示的数值为:(+1)+(﹣1)=0,则可推算图2表示的数值为( )
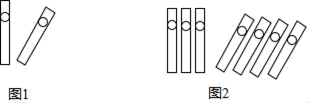 A、7 B、﹣1 C、1 D、±13. 一个几何体的侧面展开图如图所示,则该几何体的底面是( )
A、7 B、﹣1 C、1 D、±13. 一个几何体的侧面展开图如图所示,则该几何体的底面是( )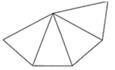 A、
A、 B、
B、 C、
C、 D、
D、 4. 2022年10月16日上午10时,中国共产党第二十次全国代表大会开幕,习近平代表第十九届中央委员会向党的二十大作报告,报告中提到,十年来,我国人均国内生产总值从三万九千八百元增加到八万一千元,八万一千用科学记数法可以表示为( )A、 B、 C、 D、5. 数轴上-2.1和3.9之间的整数有( )A、4个 B、5个 C、6个 D、7个6. 如图,小红做了 4 道判断题每小题答对给10 分,答错不给分,则小红得分为( )
4. 2022年10月16日上午10时,中国共产党第二十次全国代表大会开幕,习近平代表第十九届中央委员会向党的二十大作报告,报告中提到,十年来,我国人均国内生产总值从三万九千八百元增加到八万一千元,八万一千用科学记数法可以表示为( )A、 B、 C、 D、5. 数轴上-2.1和3.9之间的整数有( )A、4个 B、5个 C、6个 D、7个6. 如图,小红做了 4 道判断题每小题答对给10 分,答错不给分,则小红得分为( ) A、0 B、10 C、20 D、307. 小刚同学设计了一种“幻圆”游戏,将分别填入图中的圆圈内,使横、竖以及内外两圈上的4个数之和都相等,他已经将这五个数填入了圆圈,则图中a+b的值为( )
A、0 B、10 C、20 D、307. 小刚同学设计了一种“幻圆”游戏,将分别填入图中的圆圈内,使横、竖以及内外两圈上的4个数之和都相等,他已经将这五个数填入了圆圈,则图中a+b的值为( ) A、 B、 C、 D、8. 如图,在一个正方体纸盒上切一刀,切面与棱的交点分别为 , , , 切掉角后,将纸盒剪开展成平面,则展开图不可能是( )
A、 B、 C、 D、8. 如图,在一个正方体纸盒上切一刀,切面与棱的交点分别为 , , , 切掉角后,将纸盒剪开展成平面,则展开图不可能是( )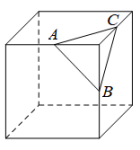 A、
A、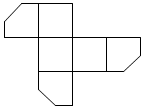 B、
B、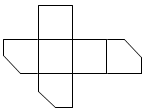 C、
C、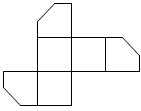 D、
D、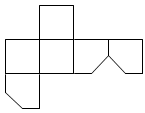
二、填空题
-
9. 2020年6月9日,我国全海深自主遥控潜水器“海斗一号”在马里亚纳海沟刷新了我国潜水器下潜深度的纪录,最大下潜深度达10907米.假设以马里亚纳海沟所在海域的海平面为基准,记为0米,高于马里亚纳海沟所在海域的海平面100米的某地的高度记为 米,根据题意,“海斗一号”下潜至最大深度10907米处,该处的高度可记为米.10. 六棱柱有条棱.11. 比较大小: . (用“>”“<”“=”填空)12. 请写出一个系数是 , 次数是3的单项式: .13. 若 , 互为倒数,则的值为 .14. 甲、乙、丙三家超市为了促销一种定价为x元的商品,甲超市连续两次降价 ;乙超市一次性降价 ;丙超市第一次降价 ,第二次降价 ;顾客要购买这种商品,最划算的超市是.15. 如图,将两张边长分别为和的正方形纸片分别按图①和图②两种方式放置在长方形内(图①和图②中两张正方形纸片均有部分重叠),未被这两张正方形纸片覆盖的部分用阴影表示.若长方形中边 , 的长度分别为 , . 设图①中阴影部分面积为 , 图②中阴影部分面积为 , 当时,的值为 .
 16. 如图,模块①由15个棱长为1的小正方体构成,模块②一⑥均由4个棱长为1的小正方体构成,现在从模块②一⑥中选出三个模块放到模块①上,与模块①组成一个棱长为3的大正方体,则符合上述要求的三个模块序号是 .
16. 如图,模块①由15个棱长为1的小正方体构成,模块②一⑥均由4个棱长为1的小正方体构成,现在从模块②一⑥中选出三个模块放到模块①上,与模块①组成一个棱长为3的大正方体,则符合上述要求的三个模块序号是 .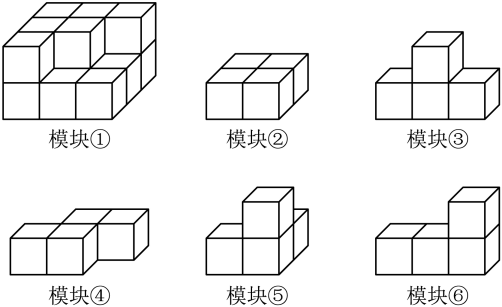
三、解答题
-
17. 计算化简:(1)、计算:;(2)、计算:;(3)、计算:;(4)、化简:;(5)、化简:;(6)、先化简,再求值:;其中 , .18. 有筐白菜,以每筐千克为标准,超过的千克数记作正数,不足的千克数记作负数,称后的记录如下:







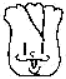
回答下列问题:
(1)、这8筐白菜中,最接近25千克的那筐白菜为 千克;(2)、以每筐千克为标准,这筐白菜总计超过或不足多少千克?(3)、若白菜每千克售价元,则售出这筐白菜可得多少元?19. 如图是一个正方体纸盒的展开图,已知这个正方体纸盒相对两个面上的代数式的值相等.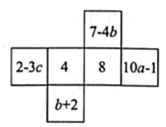 (1)、求 , , 的值;(2)、求代数式的值.20. 小明早晨跑步,他从自己家出发,向东跑了2到达小彬家,继续向东跑了1.5到达小红家,然后又向西跑了4.5到达学校,最后又向东,跑回到自己家.(1)、若以小明家为原点,向东的方向为正方向,用1个单位长度表示1 , 请在如图所示的数轴上,分别用点表示出小彬家,小红家和学校的位置;
(1)、求 , , 的值;(2)、求代数式的值.20. 小明早晨跑步,他从自己家出发,向东跑了2到达小彬家,继续向东跑了1.5到达小红家,然后又向西跑了4.5到达学校,最后又向东,跑回到自己家.(1)、若以小明家为原点,向东的方向为正方向,用1个单位长度表示1 , 请在如图所示的数轴上,分别用点表示出小彬家,小红家和学校的位置; (2)、小彬家与学校之间的距离为;(3)、如果小明跑步的速度是200 , 那么小明跑步一共用了多长时间?21. 用6个相同的小正方体摆成如图所示的几何体.
(2)、小彬家与学校之间的距离为;(3)、如果小明跑步的速度是200 , 那么小明跑步一共用了多长时间?21. 用6个相同的小正方体摆成如图所示的几何体.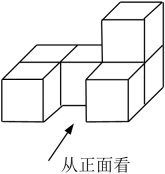 (1)、画出该几何体从正面、左面和上面看到的形状图;(2)、如果每个小正方体棱长为1,则该几何体的表面积是;(3)、在这个几何体上再添加一些相同的小正方体,如果从左面和从上面看到的形状图不变,那么最多可以再添加小正方体.22. 如表所示的数中,第个数比第个数大2(其中是正整数).
(1)、画出该几何体从正面、左面和上面看到的形状图;(2)、如果每个小正方体棱长为1,则该几何体的表面积是;(3)、在这个几何体上再添加一些相同的小正方体,如果从左面和从上面看到的形状图不变,那么最多可以再添加小正方体.22. 如表所示的数中,第个数比第个数大2(其中是正整数).第1个数
第2个数
第3个数
第4个数
第5个数
…
…
(1)、第个数可表示为;第个数可表示为;(2)、第个数是 , 第个数为 , 则 , ;(3)、第个数可表示为 .23. 如图①,A,B为数轴上不重合的两个定点,点P也在该数轴上,我们比较线段和的长度,将较短线段的长度定义为点P到线段的“靠近距离”.特别地,若线段和的长度相等,则将线段或的长度定义为点P到线段的“靠近距离”.如图②,数轴的原点为O,点A表示的数为 , 点B表示的数为4.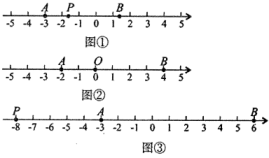 (1)、点O到线段的“靠近距离”为;(2)、点P表示的数为m,若点P到线段的“靠近距离”为7,则m的值为 .(3)、如图③,在数轴上,点P表示的数为 , 点A表示的数为 , 点B表示的数为6,点P以每秒1个单位长度的速度沿数轴向正方向移动.设移动的时间为秒,当点P到线段的“靠近距离”为4.5时,求t的值.
(1)、点O到线段的“靠近距离”为;(2)、点P表示的数为m,若点P到线段的“靠近距离”为7,则m的值为 .(3)、如图③,在数轴上,点P表示的数为 , 点A表示的数为 , 点B表示的数为6,点P以每秒1个单位长度的速度沿数轴向正方向移动.设移动的时间为秒,当点P到线段的“靠近距离”为4.5时,求t的值.