山东省聊城市阳谷县2022-2023学年七年级上学期期中数学试题

试卷更新日期：2022-12-20 类型：期中考试

进入出卷网下载

一、单选题

1. 在朱自清的《春》中描写春雨“像牛毛、像花针、像细丝，密密麻麻地斜织着”的语句，这里把雨看成了线，这说明了（）

A、点动成线 B、线动成面 C、面动成体 D、以上都不对

查看试题解析
2. 如图所示，某同学的家在P处，他想尽快赶到附近C处搭顺风车，他选择第②条路线，用几何知识解释其道理正确的是（）

A、两点确定一条直线 B、两点之间，直线最短 C、两点之间，线段最短 D、经过一点有无数条直线

查看试题解析
3. 若盈余2万元记作 $+ 2$ 万元，则 $- 2$ 万元表示（）

A、盈余2万元 B、亏损2万元 C、亏损 $- 2$ 万元 D、不盈余也不亏损

查看试题解析
4. 如图，数轴上有三个点A，B，C，若点A，B表示的数互为相反数，且 $A B = 4$ ，则点C表示的数是（）

A、6 B、4 C、2 D、0

查看试题解析
5. 有理数a，b在数轴上的位置如图所示，则下列各式正确的是（）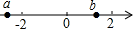

A、a+b>0 B、|a|<|b| C、ab<0 D、|a−b|=a−b

查看试题解析
6. 如图，点 $B$ 是线段 $A D$ 的中点，点 $C$ 在线段 $B D$ 上，且 $A B = a$ ， $C D = b$ ，则下列结论中错误的是（）

A、 $A D = 2 a$ B、 $B C = a - b$ C、 $A C = 2 a - b$ D、 $B C = \frac{1}{3} b$

查看试题解析
7. 下列运算结果最小的是（）

A、－1＋0.5 B、－1－0.5 C、－1×0.5 D、－1÷0.5

查看试题解析
8. 计算： $1 - (+ 2) + 3 - (+ 4) + 5 - (+ 6) + ⋯ - (+ 2022) =$ （）

A、2022 B、 $- 2022$ C、 $- 1011$ D、1011

查看试题解析
9. 已知|a|＝2，b²＝25，且ab＞0，则a﹣b的值为（　　）

A、7 B、﹣3 C、3 D、3或﹣3

查看试题解析
10. 下面调查中，适合采用普查的是（）

A、调查全国中学生心理健康现状 B、10月20日阳谷全员核酸检测 C、调查我市食品合格情况 D、调查南通电视台《今日观察》收视率

查看试题解析
11. 某校有4000名学生，随机抽取了400名学生进行体重调查，下列说法错误的是（）

A、总体是该校4000名学生的体重 B、个体是每一个学生 C、样本是抽取的400名学生的体重 D、样本容量是400

查看试题解析
12. 下列四个统计图中，用来表示不同品种的奶牛的日平均产奶量最为合适的是（）

A、 B、 C、 D、

查看试题解析

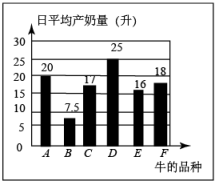
二、填空题

13. 如图图中有a条直线，b条射线，c条线段，则a+b－c的值等于．

查看试题解析
14. 将如图折叠成一个正方体，与“思”字相对的面上的字是．

查看试题解析
15. 比较大小：－ $\frac{5}{6}$ － $\frac{3}{4}$ ．

查看试题解析
16. 数轴上的点A，C，B分别表示-2，4，8，若 $A C = B D$ ，则数轴上的点D表示的数是．

查看试题解析
17. 为了解某市5万名学生平均每天完成课后作业的时间，请你运用数学的统计知识将统计的主要步骤进行排序：
①得出结论，提出建议；
②分析数据；
③从5万名学生中随机抽取500名学生，调查他们平均完成课后作业的时间；
④利用统计图表将收集的数据整理和表示．
合理的排序是

查看试题解析
18. 2022年春节前夕，学校向2000名学生发出“减少空气污染，少放烟花爆竹”倡议书，并围绕“A类：不放烟花爆竹；B类：少放烟花爆竹；C类：使用电子鞭炮；D类：不会减少烟花爆竹数量”四个选项进行问卷调查（单选），并对100名学生的调查结果绘制成统计图（如图所示）．根据抽样结果，估计全校“使用电子鞭炮”的学生有名．

查看试题解析

三、解答题

19. 如图，点B，D都在线段AC上，AB＝18，点D是线段AB的中点，BD＝3BC，求AC的长．

查看试题解析
20. 把下列各数填在相应的集合中：8，－1，－0.4， $\frac{3}{5}$ ， 0， $\frac{1}{3}$ ， $- 1 \frac{3}{7}$ ， $- (- 5)$ ， $- | - \frac{20}{7} |$ ．
正数集合{    …}；
负数集合{    …}；
整数集合{    …}；
分数集合{        …}；
非负有理数集合{         …}．

查看试题解析
21. 薛老师坚持跑步锻炼身体，他以 $30 m i n$ 为基准，超过 $30 m i n$ 的部分计为“+”，不足 $30 m i n$ 的部分计为“-”，将连续7天的跑步时间（单位： $m i n$ ）记录如下：
星期
一
二
三
四
五
六
日
与30分钟差值
$+ 10$
$- 8$
$+ 12$
$- 6$
$+ 11$
$+ 14$
$- 3$

(1)、薛老师跑步时间最长的一天比最短的一天多跑几分钟？

(2)、若薛老师跑步的平均速度为 $0.1 k m / m i n$ ，请计算这七天他共跑了多少 $k m$ ？

查看试题解析
22. 根据实际规律我们知道：海拔高度每升高100米，气温将下降0.6℃．甲、乙两名登山运动员在攀登同一座高峰，途中甲发信息说他所在地的气温为5℃，海拔为1200米，同一时刻乙发回信息说他所在地气温为-4℃．（设地面海拔为0米）

(1)、求此刻地面的气温为多少℃；

(2)、求乙所在地的海拔高度．

查看试题解析
23. 计算

(1)、 $- 4^{2} - 3 \times 2^{2} \times (\frac{1}{3} - \frac{1}{2}) \div (- 1 \frac{1}{3})$ ；

(2)、 $- 1^{2022} + 24 \div (- 2)^{3} - 3^{2} \times {(- \frac{1}{3})}^{2}$ ．

查看试题解析
24. 如图，点C在线段AB上， $A C < C B$ ，点D、E分别是AB和CB的中点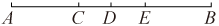， $A C = 10 c m$ ， $E B = 8 c m$ .

(1)、求线段CD，DE，AB的长；

(2)、是否存在点M，使它到A，C两点的距离之和等于8cm，为什么？

(3)、是否存在点M，使它到A，C两点的距离之和大于10cm？如果点M存在，点M的位置应该在哪里？为什么？这样的点M有多少个？

查看试题解析
25. 为进一步开展“睡眠管理”工作，某校对部分学生的睡眠情况进行了问卷调查．设每名学生平均每天的睡眠时间为x小时，其中的分组情况是：
A组： $x < 8.5$ B组： $8.5 \leq x < 9$

C组： $9 \leq x < 9.5$ D组： $9.5 \leq x < 10$ E组： $x \geq 10$

根据调查结果绘制成两幅不完整的统计图，请根据图中提供的信息，解答下列问题：

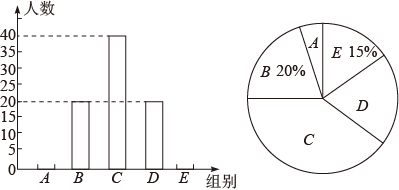(1)、本次共调查了名学生；

(2)、补全条形统计图；

(3)、在扇形统计图中，求D组所对应的扇形圆心角的度数；

(4)、若该校有1500名学生，请估计该校睡眠时间不足9小时的学生有多少人？

查看试题解析
26. 某校想调查学生对跳绳运动的意见，特向八年级的300名学生作问卷调查，其结果如下：
意见
非常喜欢
喜欢
有一点喜欢
不喜欢
人数
135
60
60
45

(1)、请用条形统计图表示表中描述的信息；

(2)、请用扇形统计图表示各种意见占总调查人数的百分比情况；

(3)、从你画的统计图表中你能得出什么结论．

查看试题解析

星期	一	二	三	四	五	六	日
与30分钟差值	$+ 10$	$- 8$	$+ 12$	$- 6$	$+ 11$	$+ 14$	$- 3$

意见	非常喜欢	喜欢	有一点喜欢	不喜欢
人数	135	60	60	45