山东省济南市市中区2022-2023学年七年级上学期期中数学试题

试卷更新日期：2022-12-20 类型：期中考试

进入出卷网下载

一、单选题

1. 2022的相反数是（）

A、 $\frac{1}{2022}$ B、 $- \frac{1}{2022}$ C、 $2022$ D、 $- 2022$

查看试题解析
2. 如图所示图形绕直线旋转一周，可以得到圆柱的是（）

A、 B、 C、 D、

查看试题解析
3. 党的十八大以来，以习近平同志为核心的党中央重视技能人才的培育与发展．据报道，截至2021年底，我国高技能人才超过65000000人，将数据65000000用科学记数法表示为（）

A、 $6.5 \times 1 0^{6}$ B、 $65 \times 1 0^{6}$ C、 $0.65 \times 1 0^{8}$ D、 $6.5 \times 1 0^{7}$

查看试题解析
4. 某品牌大米包装袋上印有【（9±0.10）（kg）】字样．即标准重量为9kg，上下偏差不超过0.1kg就符合标准．则下列不符合标准的是（）

A、9.15kg B、8.95kg C、9.05kg D、8.90kg

查看试题解析
5. 用一个平面去截一个三棱柱，不能得到的截面形状是（）

A、等边三角形 B、长方形 C、梯形 D、六边形

查看试题解析
6. 多项式 $\frac{1}{2} x^{6} y^{2} - 2 x^{3} y^{4} + 3$ 的次数和项数分别为（）

A、 $7 ， 2$ B、 $8 ， 3$ C、 $8 ， 2$ D、 $7 ， 3$

查看试题解析
7.
一个正方体的平面展开图如图所示，每一个面都有一个汉字，则在该正方体中和“国”字相对的汉字是（　　）

A、追 B、逐 C、梦 D、想

查看试题解析
8.
已知有理数a、b在数轴上的位置如图所示，下列结论正确的是（）

A、a＞b B、ab＜0 C、b－a＞0 D、a＋b＞0

查看试题解析
9. 已知有2个完全相同的边长为a、b的小长方形和1个边长为m、n的大长方形，小明把这2个小长方形按如图所示放置在大长方形中，小明经过推事得知，要求出图中阴影部分的周长之和，只需知道a、b、m、n中的一个量即可，则要知道的那个量是（）

A、a B、b C、m D、n

查看试题解析
10. 定义一种对正整数n的“F”运算：①当n为奇数时，结果为 $3 n + 5$ ；②当n为偶数时，结果为 $\frac{n}{2^{k}}$ （其中k是使 $\frac{n}{2^{k}}$ 为奇数的最大正整数），并且运算可以重复进行，例如如图所示为 $n = 26$ 时的运算过程，若 $n = 49$ ，则第 $2022$ 次“F”运算的结果是（）

A、152 B、49 C、62 D、31

查看试题解析

二、填空题

11. 单项式 $- 2 x^{4} y$ 的系数是．

查看试题解析
12. 比较大小：-4-3．（填＞或＜号）

查看试题解析
13. 一个棱柱有10个面，且所有侧棱的和为40cm，则每条侧棱长为cm．

查看试题解析
14. 如图是一组有规律的图案，第1个图案由4个基础图形组成，第2个图案由7个基础图形组成，…，第100个图案中的基础图形个数为．

查看试题解析
15. 已知 $x^{2} - 2 x - 3 = 0$ ，则 $7 + x^{2} - 2 x =$ ．

查看试题解析
16. x是不为1的有理数，我们把 $\frac{1}{1 - x}$ 称为x的差倒数．现有若干个数，第一个数记为 $a_{1}$ ，第二个数记为 $a_{2}$ ，第3个数记为 $a_{3}$ ， …，第n个数记为 $a_{n}$ ，已知 $a_{1}$ ＝-0.5， $a_{2}$ 是 $a_{1}$ 的差倒数， $a_{3}$ 是 $a_{2}$ 的差倒数……以此类推．则 $a_{1009} - a_{1011}$ ＝．

查看试题解析

三、解答题

17. 图1是由7个小正方体（每个小正方体的棱长都是1）所堆成的几何体．请画出这个儿何体从正面、左面、上面三个方向看到的形状图；

查看试题解析
18. 在数轴上表示下列各数： $\frac{1}{2} ， - 3.5 ， - 1.6 ， - \frac{1}{3} ， - 4 ， 2.5$ ．并用“<”把这些数连接起来．

查看试题解析
19. 如图，是一个几何体的表面展开图，依据图中数据求该几何体的表面积和体积．

查看试题解析
20. 计算：

(1)、 $2 - (- 4) + (- 1)$

(2)、 $- \frac{6}{7} \times (- 15) \div (- \frac{6}{7})$

(3)、 $- 1^{2022} - (\frac{7}{12} - \frac{5}{6}) \times | - 24 |$

(4)、 $(- 36) \times (\frac{1}{3} - \frac{1}{2}) + 16 \div (- 2)^{3}$

查看试题解析
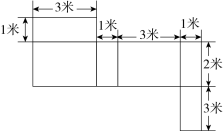21. 高速公路养护小组，乘车沿东西向公路巡视维护，如果约定向东为正，向西为负，当天的行驶记录如下（单位：千米）： $+ 17$ ， $- 9$ ， $+ 7$ ， $- 15$ ， $- 3$ ， $+ 11$ ， $- 6$ ， $- 8$ ， $+ 5$ ， $+ 16$

(1)、养护小组最后到达的地方在出发点的哪个方向？距出发点多远？

(2)、若汽车耗油量为0.5升/千米，则这次养护共耗油多少升？

查看试题解析
22. 化简：

(1)、 $5 x - 4 y - 3 x + y$

(2)、 $2 a - (4 a + 5 b) + 2 (3 a - 4 b)$

查看试题解析
23. 有理数a，b，c在数轴上的位置如图所示

(1)、a0；b0；c0．

(2)、化简 $| a | + | a + b | - | c - b |$ ．

查看试题解析
24. 已知 $A = b^{2} - a^{2} + 5 a b$ ， $B = 3 a b + 2 b^{2} - a^{2}$ ．

(1)、化简： $2 A - B$ ；

(2)、当 $a = - 1$ ， $b = 2$ 时，求 $2 A - B$ 的值．

查看试题解析
25. 综合与探究：
【概念学习】
现规定：求若干个相同的有理数（均不等于0）的商的运算叫做除方，比如 $2 \div 2 \div 2$ ， $(- 3) \div (- 3) \div (- 3) \div (- 3)$ 等，类比有理数的乘方，我们把 $2 \div 2 \div 2$ 写作 $2^{③}$ ，读作“2的圈3次方”， $(- 3) \div (- 3) \div (- 3) \div (- 3)$ 写作 ${(- 3)}^{④}$ ，读作“ $(- 3)$ 的圈4次方”，一般地把 $\frac{a \div a \div a \div ⋯ \div a}{n 个 a} (a \neq 0)$ 写作 $a^{ⓝ}$ ，读作“a的圈n次方”．

(1)、【初步探究】
直接写出计算结果： $2^{③}$ =； ${(- \frac{1}{2})}^{③}$ = ．

(2)、【深入思考】
我们知道，有理数的减法运算可以转化为加法运算，除法运算可以转化为乘法运算，那么有理数的除方运算如何转化为乘方运算呢？
除方→ $2^{④}$ $= 2 \div 2 \div 2 \div 2 = 2 \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} = {(\frac{1}{2})}^{2}$ →乘方幂的形式
试一试：仿照上面的算式，把下列除方运算直接写成幂的形式： ${(- 3)}^{⑤}$ = ， ${(\frac{1}{5})}^{⑥}$ = ．

(3)、算一算： $1 2^{2} \div {(- \frac{1}{3})}^{④} \times (- 2)^{⑥} - {(- \frac{1}{3})}^{⑥} \div 3^{3}$ ．

查看试题解析
26. 已知数轴上三点M，O，N对应的数分别为 $- 1$ ， 0，3，点P为数轴上任意一点，其对应的数为x，

(1)、MN的长为；

(2)、如果点P到点M、点N的距离相等，那么x的值是；

(3)、数轴上是否存在点P，使点P到点M、点N的距离之和是8？若存在，直接写出x的值；若不存在，请说明理由，

(4)、如果点P以每分钟1个单位长度的速度从点O向左运动，同时点M和点N分别以每分钟2个单位长度和每分钟3个单位长度的速度也向左运动，设t分钟时点P到点M、点N的距离相等，求t的值，

查看试题解析