山东省济南市历城区2022-2023学年七年级上学期期中考试数学试题

试卷更新日期：2022-12-20 类型：期中考试

进入出卷网下载

一、单选题

1. $- 3$ 的绝对值是（）

A、3 B、 $\frac{1}{3}$ C、 $- \frac{1}{3}$ D、 $- 3$

查看试题解析
2. 北京冬奥会标志性场馆国家速滑馆“冰丝带”近12000平方米的冰面采用分模块控制技术，可根据不同项目分区域、分标准制冰．将12000用科学记数法表示为（）

A、 $0.12 \times 1 0^{5}$ B、 $1.2 \times 1 0^{5}$ C、 $1.2 \times 1 0^{4}$ D、 $12 \times 1 0^{3}$

查看试题解析
3. 将下列平面图形绕轴旋转一周，可得到图中所示的立体图形的是（）

A、 B、 C、 D、

查看试题解析
4. 在苏果超市，某品牌的食品包装袋上“质量”标注：500g±10g下列待检查的各袋食品中质量合格的是（　　）

A、530g B、515g C、480g D、495g

查看试题解析
5. 用一个平面去截下列的几何体，可以得到长方形截面的几何体有（）

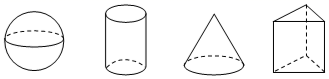A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 如果 $2 x^{2 m} y^{6}$ 与 $- 3 x^{8} y^{2 n}$ 是同类项，那么m、n的值分别为（）

A、 $m = 4 ， n = 3$ B、 $m = - 2 ， n = 3$ C、 $m = 3 ， n = 2$ D、 $m = 4 ， n = 4$

查看试题解析
7. 已知2a-3b＝2，则5-6a+9b的值是（）

A、0 B、2 C、-1 D、1

查看试题解析
8. 有理数a，b在数轴上对应的位置如图所示，则（）

A、 $| a | < | b |$ B、 $a b > 0$ C、 $a + b < 0$ D、 $a - b > 0$

查看试题解析
9. 若 $x^{2} = 9 ， | y | = 7$ ，且 $x > y$ ，则 $x + y$ 的值为（）

A、 $- 4$ 或 $- 10$ B、 $- 4$ 或10 C、4或10 D、4或 $- 10$

查看试题解析
10. 将正偶数按下表排成5列：

第1列
第2列
第3列
第4列
第5列
第1行
2
4
6
8
第2行
16
14
12
10
第3行
18
20
22
24

28
26

若2022在第m行第n列，则 $m + n =$ （）

A、256 B、257 C、510 D、511

查看试题解析

二、填空题

11. 单项式 $4 a^{3} b^{2}$ 的次数是．

查看试题解析
12. 如图，在正方体表面展开图的每个面内都写有1个汉字，则该正方体中与“胜”相对的字是．

查看试题解析
13. 一本笔记本原价a元，降价后比原来便宜了b元，小玲买了3本这样的笔记本，比原来便宜了元．

查看试题解析
14. 若 $| x - 2 |$ 与 $| 2 y + 6 |$ 互为相反数，则 $x + y =$ ．

查看试题解析
15. 如图是一个运算程序的示意图，若开始输入的x值为81，我们看到第一次输出的结果为27，第二次输出的结果为9，则第8次输出的结果为．

查看试题解析
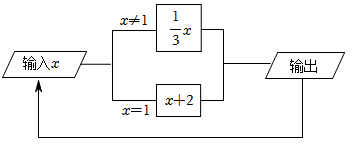16. 有依次排列的3个数：2，6，7，对任意相邻的两个数，都用右边的数减去左边的数，所得之差写在这两个数之间，可产生一个新数串：2，4，6，1，7，这称为第一次操作；做第二次同样的操作后也产生一个新数串：2，2，4，2，6， $- 5$ ， 1，6，7，若相继依次操作，则从数串：2，6，7开始操作第100次时所产生的那个新数串的所有数之和是．

查看试题解析

三、解答题

17. 在数轴上表示下列各数， $3.5 ， - \frac{1}{2} ， 1 \frac{1}{2} ， - 4 ， - 2.5$ ．并用“＜”把这些数连接起来．

查看试题解析
18. 计算题

(1)、 $- 20 + (- 14) - (- 18)$ ；

(2)、 $(- \frac{3}{8} - \frac{1}{6} + \frac{3}{4}) \times (- 24)$ ；

(3)、 $- 8 \div 2 \times (- \frac{1}{2}) \times 0.25$ ；

(4)、 $- 1^{4} - 8 \div (- 4) \times | - 6 + 4 |$ ．

查看试题解析
19.

(1)、化简： $m - n + 5 m - 4 n$

(2)、化简： $3 (x^{2} - 2 y) - \frac{1}{2} (6 x^{2} - 14 y) + 10$ ．

(3)、先化简，再求值： $2 x^{2} + 4 y^{2} + (2 y^{2} - 3 x^{2}) - 2 (y^{2} - 2 x^{2}) ，$ ，其中 $x = - 1 ， y = \frac{1}{2}$ ．

查看试题解析
20. 如图是由一些棱长都为1cm的小正方体组合成的简单几何体．

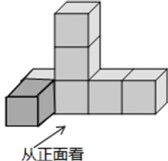
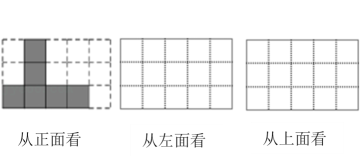(1)、从正面看该几何体，看到的形状图如图所示，请在下面方格纸中分别画出从左面看和从上面看该几何体看到的形状图；（画出的图需涂上阴影或斜线）

(2)、如果在这个几何体上再添加一些小正方体，并保持从左面看和从上面看观察到的形状图不变，最多可以再添加块小正方体．

查看试题解析
21. 李强靠勤工俭学的收入维持上大学的费用．下面是他某一周的收支情况表（收入为正，支出为负，单位为元）
周一
周二
三
四
五
六
日
+15
+10
0
+20
+15
+10
+14
-8
-12
-19
-10
-9
-11
-8

(1)、到这个周末，李强有多少节余？

(2)、照这样，李强一个月（按30天计算）能有多少节余？

(3)、按以上的支出水平，李强一个月（按30天计算）至少有多少收入才能维持正常开支？

查看试题解析
22. 为了提高居民的宜居环境，某小区规划修建一个广场（平面图如图中阴影部分所示）．

(1)、用含m，n的式子表示广场（阴影部分）的周长C和面积S；

(2)、若 $m = 30$ 米， $n = 20$ 米，修建每平方米需费用200元，求修建广场的总费用W的值．

查看试题解析
23. 已知 $A = 2 a^{2} + 3 a b - 2 a - 1$ ， $B = - a^{2} + 12 a b + 2$

(1)、化简 $4 A - (3 A - 2 B)$

(2)、若（1）中式子的值与a的取值无关，求b的值

查看试题解析
24. 利用图形来表示数量或数量关系，也可以利用数量或数量关系来描述图形特征或图形之间的关系，这种思想方法称为数形结合．请你尝试利用数形结合的思想方法解决下列问题

(1)、如图①，一个边长为1的正方形，依次取正方形面积的 $\frac{1}{2} ， \frac{1}{4} ， \frac{1}{8} ⋯ \frac{1}{2^{n}}$ ，根据图示我们可以知道： $\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + ⋯ + \frac{1}{2^{n}}$ ＝．（用含有n的式子表示）

(2)、如图②，一个边长为1的正方形，第一次取正方形面积的 $\frac{2}{3}$ ，然后依次取剩余部分的 $\frac{2}{3}$ ，根据图示：计算： $\frac{2}{3} + \frac{2}{9} + \frac{2}{27} + ⋯ + \frac{2}{3^{n}}$ ＝．（用含有n的式子表示）

(3)、如图③是一个边长为1的正方形，根据图示：计算： $\frac{1}{3} + \frac{2}{9} + \frac{4}{27} + \frac{8}{81} + ⋯ + \frac{2^{n - 1}}{3^{n}}$ ＝．（用含有n的式子表示）

查看试题解析
25. 如图，点A、B、C在数轴上，它们对应的数分别是a、b、c，已知a的相反数是8．一个点从数轴上的原点向右移动4个单位到达B点，从B点再向右移动5个单位到达C点．

(1)、写出a＝；b＝；c＝．

(2)、若甲、乙、丙三个动点分别从A、B、C三点同时出发沿数轴负方向运动，它们的速度分别是4、1、2（单位/秒），运行t秒后，甲、乙、丙三个动点位置的对应数分别为： $x_{甲} ， x_{乙} ， x_{丙} ，$ ，当 $t > 5$ 时，求式子 $\frac{| x_{甲} - x_{乙} | + | x_{乙} - x_{丙} | - | x_{甲} - x_{丙} |}{t - 5}$ 的值．

(3)、若甲、乙、丙三个动点分别从A、B、C三点同时出发沿数轴正方向运动，它们的速度分别是4、1、2（单位/秒），运动多长时间时，丙与甲、乙等距离？

查看试题解析

	第1列	第2列	第3列	第4列	第5列
第1行		2	4	6	8
第2行	16	14	12	10
第3行		18	20	22	24
			28	26

周一	周二	三	四	五	六	日
+15	+10	0	+20	+15	+10	+14
-8	-12	-19	-10	-9	-11	-8