广东省深圳市2021-2022学年第二学期学科素养形成七年级数学阶段巩固一
试卷更新日期：2022-12-20 类型：月考试卷
一、选择题(共10小题，共30分)
-
1. 下列运算正确的是（ ）A、(a-b)2=a2-b2 B、(a3)2=a5 C、a5÷a3=a2 D、a3+a2=a52. 科学家借助电子显微镜发现新型冠状病毒的平均直径约为0.000000125米，则数据0.000000125用科学记数法表示正确的是（ ）A、1.25×108 B、1.25×10-8 C、1.25×107 D、1.25×10-73. 下列说法中，正确的是（ ）A、从直线外一点到这条直线的垂线段，叫做这个点到这条直线的距离 B、平面内，互相垂直的两条直线不一定相交 C、过一点有且只有一条直线垂直于已知直线 D、直线AB外一点P与直线上各点连接而成的所有线段中最短线段的长是7cm，则点P到直线AB的距离是7cm4. 如图，直线DE分别交射线BA，BG于点D，F，则下列条件中能判定DE∥BC的个数是（ ）
①∠ADE=∠GBC；②∠DFB=∠GBC；③∠EDB+∠ABC=180°；④∠GFE=∠GBC．
A、1 B、2 C、3 D、45. 如图，已知直线m∥n，线段AB的两个端点A，B分别落在直线m，n上，将线段AB绕点A按逆时针方向旋转80°得到线段AC，连接BC．若∠1=30°，则∠2的度数为（ ）
A、15° B、20° C、25° D、30°6. 如图，点C在∠AOB的OB边上，用尺规作出了∠BCD=∠AOB．以下是排乱的作图过程：①以点C为圆心，OE长为半径画 ， 交OB于点M．②作射线CD，则∠BCD=∠AOB．③以点M为圆心，EF长为半径画弧，交于点D．④以点O为圆心，任意长为半径画 ， 分别交OA，OB于点E，E则正确的作图顺序是（ ）
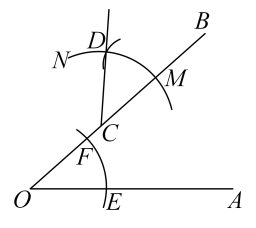A、①②③④ B、③②④① C、④①③② D、④③①②7. 已知(－x)(2x2－ax－1)－2x3＋3x2中不含x的二次项，则a的值是（ ）A、3 B、2 C、-3 D、-28. 若a=0.32 ， b=-3-2 ， c=()-2 ， d=()0 ， 则（ ）A、a<b<c<d B、a<d<c<b C、b<a<d<c D、c<a<d<b9. 长方形面积是3a2-3ab+6a，一边长为3a，则它的周长为（ ）A、2a-b+2 B、8a-2b C、8a-2b+4 D、4a-b+210. 有若干个大小形状完全相同的小长方形，现将其中4个如图1摆放，构造出一个正方形，其中阴影部分面积为35；其中5个如图摆放，构造出一个长方形，其中阴影部分面积为102(各个小长方形之间不重叠、不留空)，则每个小长方形的面积为（ ）
A、4 B、8 C、12 D、16二、填空题(每题3分，共15分)
-
11. 已知关于x，y的多项式x2-2kxy+16y是完全平方式，则k=12. 若2x+3y-2=0，则9x·27y的值是.13. 如图，已知EF⊥AB，∠1=26°，则当AB∥CD时，∠2=.
14. 如图，直线a∥b，三角尺(各角分别为：30°，60，90°)如图摆放，若∠1=52°，则∠2的度数为
15. 数学活动课上，小明同学尝试将正方形纸片剪去一个小正方形，剩余部分沿虚线剪开，拼成新的图形。现给出下列3种不同的剪、拼方案，其中能够验证平方差公式的方案是 。(请填上正确的序号)
三、解答题(共55分)
-
16. 计算：已知(x+y)2=1，(x-y)2=49，求x2+y2和xy的值．17. 阅读下列文字，并解决问题。
已知x2y=3，求2xy（x5y2-3x3y-4x）的值.
分析：考虑到满足x2y=3的x，y的可能值较多，不可以逐一代入求解，故考虑整体思想，将x2y=3整体代入.
解：2xy（x5y2-3x3y-4x）
=2x6y3-6x4y2-8x2y
=2（x2y）3-6（x2y）2-8x2y，
将x2y=3代入
原式=2×33-6×32-8×3=-24.
请你用上述方法解决下面问题：
已知ab=3，求（2a3b2-3a2b+4a）·（-2b）的值.
18. 如图，已知：CD平分∠ACB，AC∥DE，CD∥EF，求证：EF平分∠DEB．
证明：∵CD平分∠ACB (已知)，
∴∠DCA=∠DCE(角平分线的定义)．
∵AC∥DE (已知)，
∴∠DCA= ▲
∴∠DCE=∠CDE (等量代换) ．
∵CD∥EF(已知)，
∴ ▲ =∠CDE（ ），
∠DCE=∠BEF（ ），
∴ ▲ = ▲ (等量代换)，
∴EF平分∠DEB（ ）
19. 如图，∠AOB是花园内两条小路组成的角，点C在OA上，点D在OB上，现在过点C、点D分别建一条平行于 OB和OA的小路，请用尺规在图上画出它的位置．
20. 已知：如图， ， .求证： ∥ .
21. 我国古代数学的许多发现都曾位居世界前列，其中“杨辉三角”就是一例．如图，这个三角形的构造法则：两腰上的数都是1，其余每个数均为其上方左右两数之和，它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律．例如，在三角形中第三行的三个数1，2， 1，恰好对应(a+b)2=a2+2ab+b2展开式中的系数；第四行的四个数1，3，3，1，恰好对应着(a+b)3=a3+3a2b+3ab2+b3展开式中的系数等等．
(1)、根据上面的规律，写出(a+b)5的展开式．(2)、利用上面的规律计算：25-5×24+10×23-10×22+5×2-1．22. 阅读材料：
（1）1的任何次幂都为1；
（2）-1的奇数次幂为-1；
（3）-1的偶数次幂为1；
（4）任何不等于零的数的零次幂为1．请问当x为何值时，代数式(2x+3)x+2020的值为1．
23. 如图，AB∥CD，定点E，F分别在直线AB，CD上，在平行线AB，CD之间有一动点P，满足0°<∠EPF<180° ．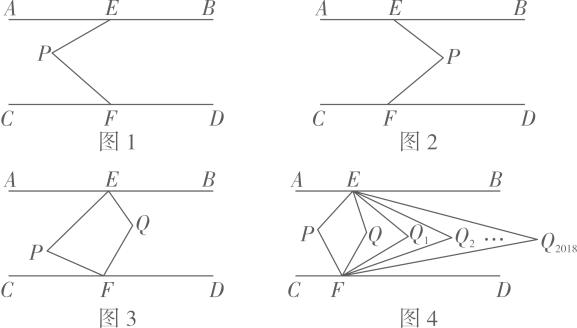
(1)、试问∠AEP，∠EPF，∠PFC满足怎样的数量关系？解：由于点P是平行线AB， CD之间的一动点，因此需要对点P的位置进行分类讨论：
如图1，当点P在EF的左侧时，∠AEP，∠EPF，∠PFC满足数量关系为
如图2，当点P在EF的右侧时，∠AEP，∠EPF，∠PFC满足数量关系为
(2)、如图3，QE，QF分别平分∠PEB和∠PFD， 且点P在EF左侧．①若∠EPF=60°，则∠EQF= ．
②猜想∠EPF与∠EQF的数量关系，并说明理由；
③如图4，若∠BEQ与∠DFQ的平分线交于点Q1 ， ∠BEQ1与∠DFQ1的平分线交于点Q2 ， ∠BEQ2与∠DFQ2的平分线交于点Q；依次类推，则∠EPF与∠EQ2018F满足怎样的数量关系？(直接写出结果)