广东省深圳市数学2022-2023学年第一学期七年级期中试题

试卷更新日期：2022-12-20 类型：期中考试

进入出卷网下载

一、选择题：本大题共10小题，每小题3分，共30分。

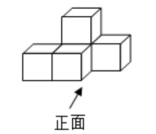
1. 2022的相反数是（）

A、 $- \frac{1}{2022}$ B、-2022 C、 $\frac{1}{2022}$ D、2022

查看试题解析
2. 如图是由5个相同的正方体搭成的几何体，这个几何体的俯视图是（）

A、 B、 C、 D、

查看试题解析
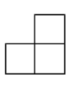3. 下列运算正确的是（）

A、5m+n=5mn B、4m-n=3 C、3n²+2n³=5n⁵ D、-m²n+2m²n=m²n

查看试题解析
4. 一个正方体的表面展开图如图所示，六个面上各有一字，连起来的意思是“全面落实双减”，把它折成正方体后，与“落”相对的字是（）

A、双 B、减 C、全 D、面

查看试题解析
5. 如图，数轴上的整数a被星星遮挡住了，则-a的值是（）

A、1 B、2 C、-2 D、-1

查看试题解析
6. 已知x-y=1，则代数式3x-3y+1的值是（）

A、2 B、-2 C、4 D、-4

查看试题解析
7. 用一个平面去截一个三棱柱，所得截面的边数最少是a条，最多是b条，下列的选项中正确的是（）

A、a=3，b=6 B、a=2，b=5 C、a=4，b=6 D、a=3，b=5

查看试题解析
8. 下列说法正确的是（）

A、用一个平面去截一个圆锥不能得到一个三角形 B、-3.5是负分数 C、单项式 $\frac{3 x^{2}}{π}$ 的系数是3 D、-3³的底数是-3

查看试题解析
9. 某商场举行促销活动，促销的方法是“消费超过200元时，所购买的商品按原价打8折后，再减少20元”。若某商品的原价为x(x>200)元，则购买该商品实际付款的金额是（）

A、(80%x-20)元 B、80%(x-20)元 C、(20%x-20)元 D、20%(x-20)元

查看试题解析
10. a是不为2的有理数，我们把 $\frac{2}{2 - a}$ 称为a的“哈利数”，如3的“哈利数”是 $\frac{2}{2 - 3}$ =-2，-2的“哈利数”是 $\frac{2}{2 - (- 2)} = \frac{1}{2}$ .已知a₁=3，a₂是a₁的“哈利数”，a₃是a₂的“哈利数”，a₄是a₃的“哈利数”，……依此类推，则a₂₀₂₃=（）

A、3 B、-2 C、 $\frac{1}{2}$ D、 $\frac{4}{3}$

查看试题解析

二、填空题：本大题共7小题，每小题4分，共28分。

11. 一次数学测试，如果80分为优秀，以80分为基准简记，例如90分记为+10，那么75分应记为分．

查看试题解析
12. “扶贫” 是新时期党和国家的重点工作之一，为落实习近平总书记提出的“精准扶贫”战略构想，某省预计三年内脱贫1020000人，数字1020000用科学记数法可表示为

查看试题解析
13. 若|a- $\frac{1}{2}$ |+|b+5|=0，则a+b的值为

查看试题解析
14. 已知 $- \frac{1}{2} x^{n} y^{2}$ 与^{$x^{3} y^{m}$}是同类项，则^{$m^{n}$}＝．

查看试题解析
15. 将一个长4cm，宽2cm的长方形绕它的长边所在的直线旋转一周，所得几何体的体积为cm³ ．

查看试题解析
16. 小颖同学到学校领来n盒粉笔，整齐地摞在讲桌上，其三视图如图，则n的值是

查看试题解析
17. 近几年来魔术风靡我国，小亮发明了一个魔术盒，把一个实数对(a，b)放入其中，就得到一个数为a²-3b+1，如把(3，2)放入其中，就得到3²-3×2+1=4，若把(-3，2)放入其中，得到数m，再把(m，4)放入其中，则得到的数是

查看试题解析

三、解答题：本大题共8小题，共62分。

18. 计算：

(1)、(-2)+(+3)-(-5)-(+4)；

(2)、 $- \frac{3}{4} \times - 8 + \frac{2}{3} - \frac{1}{6}$

(3)、100÷(-2)²-(-2)÷ $- \frac{2}{3}$

查看试题解析
19. 在数轴上表示下列各数： $\frac{1}{2}$ ， -3.5，-1.9，0，-4，-(-2)，并用“<”把这些数连接起来.

查看试题解析
20. 先化简，再求值：3x²y+[-3(x²y+1)+2xy+1]，其中x=-4，y= $\frac{1}{2}$

查看试题解析
21. 如图，从一个长方形铁皮中剪去一个小正方形，长方形的长为2a米，宽为b米，小正方形的边长为a米．

(1)、剩余铁皮的面积为平方米；(用含a、b的代数式表示)

(2)、为了防止铁皮生锈，要把剩余铁皮都喷上油漆，已知每平方米喷漆的费用为30元，当a=3，b=5时，求剩余铁皮喷漆的费用．

查看试题解析
22. 在抗洪抢险中，解放军战士的冲锋舟加满油沿东西方向的河流抢救灾民，早晨从A地出发，晚上到达B地，约定向东记为正，向西记为负，当天的航行路程记录如下(单位：千米) ：
14，-9，+8，-7，+13，-6，+12，-5．

(1)、请你通过计算帮忙确定B地相对于A地的位置；

(2)、若冲锋舟每千米耗油0.5升，油箱容量为28升，求冲锋舟当天救灾过程中至少还需补充多少升油？

查看试题解析
23. 如图，在平整的地面上，有若干个完全相同的棱长为10cm的小正方体堆成一个几何体(四面都不靠墙) ．

(1)、这个几何体由个小正方体组成．

(2)、如果在这个几何体的表面喷上黄色的漆，则在所有的小正方体中，有个正方体只有一个面是黄色，有个正方体只有两个面是黄色，有个正方体只有三个面是黄色．

(3)、这个几何体喷漆的面积为cm² ．

查看试题解析
24. 某商场销售一种西装和领带，西装每套定价1000元，领带每条定价200元．“国庆节”期间商场决定开展促销活动，活动期间向客户提供两种优惠方案(客户只能选择其中一种)：
方案一：买一套西装送一条领带；

方案二：西装和领带都按定价的90%付款．

现某客户要到该商场购买西装20套，领带x条(x>20)

(1)、若该客户按方案一购买，需付款元；若该客户按方案二购买，需付款元，(用含 x的代数式表示)

(2)、若x=30，通过计算说明此时按哪种方案购买较为合算．

查看试题解析
25. 在学习绝对值后，我们知道，|a|表示数a在数轴上的对应点与原点的距离．如：|5|表示5在数轴．上的对应点到原点的距离．而|5|=|5-0|，即|5-0|也可理解为5、0在数轴．上对应的两点之间的距离．类似的，|5-3|表示5与3之差的绝对值，也可理解为5与3两数在数轴上所对应的两点之间的距离．如|x-3|的几何意义是数轴上表示有理数3的点与表示数x的点之间的距离，一般地，点A、B在数轴上分别表示数a、b，那么A、B之间的距离可表示为|a-b|．

请根据绝对值的意义并结合数轴解答下列问题：

(1)、数轴上表示2和3的两点之间的距离是；数轴上表示 $\frac{5}{6}$ 和-5的两点之间的距离是

(2)、数轴上点P表示的数是2，P、Q两点的距离为3，则点Q表示的数是

(3)、|x+ $\frac{4}{3}$ |的几何意义是数轴上表示有理数的点与表示x的点之间的距离；

(4)、若|m-3|+|m+2|=7，则m=

(5)、数轴上有一个点表示数a，则|a+1|+|a-3|+|a+8|的最小值为

查看试题解析