2022-2023学年苏科版数学七年级上学期期末练习卷

试卷更新日期：2022-12-20 类型：期末考试

进入出卷网下载

一、单选题（每题2分，共16分）

1. 在5，0、-3、-5四个数中最小的数是（）

A、5 B、0 C、-3 D、-5

查看试题解析
2. 如图1是一个小正方体的侧面展开图，小正方体从如图2所示的位置依次翻到第1格、第2格、第3格，这时小正方体朝上面的字是（）

A、祝 B、你 C、成 D、功

查看试题解析
3. 下列计算正确的是（）

A、 $3 x^{2} + 2 x^{2} = 5 x^{4}$ B、 $3 a + 2 b = 6 a b$ C、 $a^{3} + a^{2} = a^{5}$ D、 $x^{2} - 3 x^{2} = - 2 x^{2}$

查看试题解析
4. 根据成都市统计局发布的成都上半年经济运行数据，2021年上半年实现地区生产总值9602.72亿元，同比增长13.1%，两年平均增长6.7%，全市经济稳中加固、向好．其中数字9602.72亿用科学记数法可表示为（）

A、9.60272×10¹¹ B、9.60272×10¹² C、9.60272×10¹³ D、9.60272×10¹⁴

查看试题解析
5. 如图，将一块三角形纸片剪去一部分后，发现剩余阴影部分的纸片周长要比原三角形纸片的周长大，能正确解释这一现象的数学知识是（）

A、直线没有端点，向两端无限延伸 B、两点之间，线段最短 C、经过一点有无数条直线 D、两点确定一条直线

查看试题解析
6. “汽车的雨刷在挡风玻璃上画出一个扇面”可以说是（）

A、面与面交于线 B、点动成线 C、面动成体 D、线动成面

查看试题解析
7. 某理财产品的年收益率为5.21%，定期1年，每年到期后可连本带息继续购买下一年的产品．若张老师购买了x万元该种理财产品，2年后一共拿到10万元，则根据题意列方程正确的是（）

A、 $(1 + 5.21) x = 10$ B、 ${(1 + 5.21)}^{2} x = 10$ C、 $2 (1 + 5.21 %) x = 10$ D、 ${(1 + 5.21 %)}^{2} x = 10$

查看试题解析
8. 若x、y、z是三个连续的正整数，若x²＝44944，z²＝45796，则y²＝（）

A、45369 B、45371 C、45465 D、46489

查看试题解析

二、填空题（每题2分，共20分）

9. 若 $3 x^{m} y$ 与 $- 5 x^{2} y^{n}$ 是同类项，则m＋2n＝．

查看试题解析
10. 已知n是关于x的方程 $\frac{1}{2} (1 - 4 x) = - m$ 的解，则 $2022 - 4 m + 8 n$ 的值为.

查看试题解析
11. 一个角的补角比它的余角的3倍还多10°，则这个角的度数为．

查看试题解析
12. 若 $x = 2$ 时，代数式 $a x^{3} - 5 b x - 1$ 的值为2，则 $x = - 2$ 时，代数式 $a x^{3} - 5 b x - 1$ 的值为.

查看试题解析
13. 如图是一个圆柱体的三视图，由图中数据计算此圆柱体的侧面积为．（结果保留π）

查看试题解析
14. 已知A，B，C是数轴上的三个点，点A，B表示的数分别是1，3.如图所示，若BC=2AB，则点C表示的数是．

查看试题解析
15. $48 ° 39 + 67 ° 31 =$ .

查看试题解析
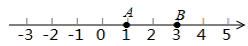16.
如图，线段AB=8cm，C是线段AB上一点，AC=3.2cm，M是AB的中点，N是AC的中点，则线段MN=cm．

查看试题解析
17. 小明在计算1－3＋5－7＋9－11＋13－15＋17时，不小心把一个运算符号写错了（“＋”错写成“－”或“－”错写成“＋”），结果算成了－17，则原式从左往右数，第个运算符号写错了.

查看试题解析
18. 小淇同学在元旦晚会上表演了一个节目：他准备了♥（红桃）和♠（黑桃）的扑克牌各10张，洗匀后将这些牌的牌面朝下，排成两列：一列m（m＞10）张，一列（20－m）张，他立刻报出长的一列中的♠（黑桃）比短的一列中的♥（红桃）多了张.（结果用含有m的代数式表示）

查看试题解析

三、解答题（共9题，共64分）

19. 计算：

(1)、 $- 10 + (- 17) - (- 23)$

(2)、 ${(- 1)}^{12} \times 6 - {(- 3)}^{3} \div (- 3) + | - 5 |$

查看试题解析
20. 先化简，再求值：3（x²﹣2xy）﹣2 $[\frac{1}{4} x y - 1 + \frac{3}{2} (- x y + x^{2})]$ ，其中x=﹣4，y= $\frac{1}{2}$ .

查看试题解析
21. 解方程：

(1)、 $4 (x - 1) = 1 - x$

(2)、 $\frac{x + 1}{3} - \frac{5 x - 1}{6} = 1$

查看试题解析
22. 如图，在6×6的正方形网格中，每个小正方形的边长都为1

（ 1 ）在图中确定三角形顶点A，B，C的位置，使AB＜BC＜CA.

（ 2 ）利用网格，作△ABC的高线CD.

（ 3 ）△ABC的面积为▲ .

查看试题解析
23. 如图，由6相同的小正方体组合成的简单几何体.

(1)、请在方格纸中分别画出几何体的主视图、左视图和俯视图；

(2)、如果在这个几何体上再添加一些相同的小正方体，并保持这个几何体的主视图和俯视图不变，那么最多可以再添加个小正方体.

查看试题解析
24. 如图，直线AB与CD相交于点O， $∠ A O E = 90 °$ .

(1)、如果 $∠ A O C = 20 °$ ，求 $∠ C O E$ 和 $∠ B O D$ 的度数.

(2)、如果 $∠ C O E = 2 ∠ B O D$ ，求 $∠ B O C$ 的度数.

查看试题解析
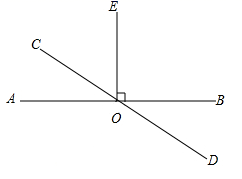25. 某机械厂甲、乙两个生产车间承担生产同一种零件的任务，甲、乙两车间共有60人，甲车间平均每人每天生产零件30个．乙车间平均每人每天生产零件20个，甲车间每天生产零件总数与乙车间每天生产零件总数之和为1400个．

(1)、求甲、乙两车间各有多少人；

(2)、该机械厂改进了生产技术，在甲、乙两车间总人数不变的情况下，从乙车间调出一部分人到甲车间．调整后甲乙车间平均每人每天生产零件都比原来多5个，甲乙两车间每天生产零件总数之和是1800个，且甲乙车间每人的计件工资分别是10元和8元，求甲乙两车间每天计件收入总和．

查看试题解析
26. 如图，将一副直角三角板的直角顶点C叠放在一起.

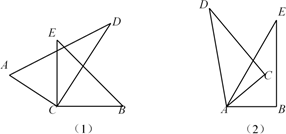(1)、如图（1），若∠DCE＝33°，则∠BCD＝， ∠ACB＝.

(2)、如图（1），猜想∠ACB与∠DCE的大小有何特殊关系？并说明理由.

(3)、如图（2），若是两个同样的直角三角板60°锐角的顶点A重合在一起，则∠DAB与∠CAE的数量关系为.

查看试题解析
27. 如图，已知直线AB和CD相交于点O，∠COE＝90°，OF平分∠AOE，∠COF＝37°.

(1)、求∠EOB的度数.

(2)、若射线OF、OD分别绕着点O按顺时针方向转动，两射线同时出发，射线OF每分钟转动6°，射线OD每分钟转动0.5°，多少分钟后，射线OF与射线OD第一次重合.

(3)、在（2）的条件下，假设转动时间不超过60分钟，若∠FOD=33°，则两射线同时出发分钟.

查看试题解析