沪科版数学九年级上册第21章二次函数与反比例函数单元过关卷
试卷更新日期:2022-12-19 类型:单元试卷
一、单选题(每题4分,共40分)
-
1. 抛物线的顶点坐标是( )A、 B、 C、 D、2. 将抛物线向左平移1个单位长度,再向上平移2个单位长度,所得到的抛物线为( )A、 B、 C、 D、3. 已知二次函数的图象上有三点 , , , 则、、的大小关系为( )A、 B、 C、 D、4. 如图,抛物线y1=ax2+bx+c与直线y2=mx+n相交于点(3,0)和(0,3),若ax2+bx+c>mx+n,则x的取值范围是( )
 A、0<x<3 B、1<x<3 C、x<0或x>3 D、x<1减x>35. 根据下列表格的对应值,判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是( )
A、0<x<3 B、1<x<3 C、x<0或x>3 D、x<1减x>35. 根据下列表格的对应值,判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是( )x
3.23
3.24
3.25
3.26
ax2+bx+c
﹣0.06
﹣0.02
0.03
0.09
A、3<x<3.23 B、3.23<x<3.24 C、3.24<x<3.25 D、3.25<x<3.266. 如图,某涵洞的截面是抛物线形,现测得水面宽AB=1.6m,涵洞顶点O与水面的距离CO是2m,则当水位上升1.5m时,水面的宽度为( ) A、1m B、0.8m C、0.6m D、0.4m7. 已知二次函数y=kx2﹣5x﹣5的图象与x轴有交点,则k的取值范围是( )A、 B、 且k≠0 C、 D、 且k≠08. 如图,在平面直角坐标系中,点P在反比例函数( , )的图象上,其纵坐标为2,过点P作//轴,交x轴于点Q,将线段绕点Q顺时针旋转60°得到线段 . 若点M也在该反比例函数的图象上,则k的值为( )
A、1m B、0.8m C、0.6m D、0.4m7. 已知二次函数y=kx2﹣5x﹣5的图象与x轴有交点,则k的取值范围是( )A、 B、 且k≠0 C、 D、 且k≠08. 如图,在平面直角坐标系中,点P在反比例函数( , )的图象上,其纵坐标为2,过点P作//轴,交x轴于点Q,将线段绕点Q顺时针旋转60°得到线段 . 若点M也在该反比例函数的图象上,则k的值为( )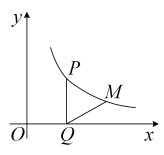 A、 B、 C、 D、49. 如图,平行四边形的顶点在双曲线上,顶点在双曲线上,中点恰好落在轴上,已知 , 则的值为( )
A、 B、 C、 D、49. 如图,平行四边形的顶点在双曲线上,顶点在双曲线上,中点恰好落在轴上,已知 , 则的值为( ) A、-8 B、-6 C、-4 D、-210. 如图所示,在平面直角坐标系中,抛物线y=-x2+2x的顶点为A点,且与x轴的正半轴交于点B,P点为该抛物线对称轴上一点,则OP+AP的最小值为( ).
A、-8 B、-6 C、-4 D、-210. 如图所示,在平面直角坐标系中,抛物线y=-x2+2x的顶点为A点,且与x轴的正半轴交于点B,P点为该抛物线对称轴上一点,则OP+AP的最小值为( ). A、3 B、 C、 D、
A、3 B、 C、 D、二、填空题(每题5分,共25分)
-
11. 若是关于x的二次函数,则m的值是 .12. 已知一个二次函数的图象开口向上,顶点坐标为 , 那么这个二次函数的解析式可以是 . (只需写一个).13. 已知二次函数 , 当时,y随x的增大而减小,则m的取值范围是 .14. 根据物理学规律,如果不考虑空气阻力,以的速度将小球沿与地面成角的方向击出,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间的函数关系是 , 当飞行时间t为s时,小球达到最高点.15. 已知抛物线 与x轴交于A , B两点(点A在点B的左侧),与y轴交于点C , 点 在抛物线上,E是该抛物线对称轴上一动点.当 的值最小时, 的面积为 .
三、综合题(共7题,共85分)
-
16. 已知二次函数y=﹣x2+6x﹣5的图象交x轴于A、B两点,点A在B左边,交y轴于点C.
 (1)、将函数y=﹣x2+6x﹣5的解析式化为y=a(x+m)2+k的形式,并指出该函数图象的开口方向、对称轴和顶点坐标;(2)、点D在该抛物线上,它是点C关于抛物线对称轴的对称点,求△ABD的面积.17. 如图,直线y=﹣x+2过x轴上的点A(2,0),且与抛物线y=ax2交于B,C两点,点B坐标为(1,1).
(1)、将函数y=﹣x2+6x﹣5的解析式化为y=a(x+m)2+k的形式,并指出该函数图象的开口方向、对称轴和顶点坐标;(2)、点D在该抛物线上,它是点C关于抛物线对称轴的对称点,求△ABD的面积.17. 如图,直线y=﹣x+2过x轴上的点A(2,0),且与抛物线y=ax2交于B,C两点,点B坐标为(1,1).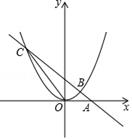 (1)、求抛物线的函数表达式;(2)、连结OC,求出△AOC的面积.(3)、当 -x+2>ax2 时,请观察图像直接写出x的取值范围.18. 如图,在 中, , , , 为 边上的动点(与 、 不重合), ,交 于点 ,连接 ,设 , 的面积为 .
(1)、求抛物线的函数表达式;(2)、连结OC,求出△AOC的面积.(3)、当 -x+2>ax2 时,请观察图像直接写出x的取值范围.18. 如图,在 中, , , , 为 边上的动点(与 、 不重合), ,交 于点 ,连接 ,设 , 的面积为 . (1)、用含 的代数式表示 的长;(2)、求 与 的函数表达式,并求当 随 增大而减小时 的取值范围.19. 如图,反比例函数与正比例函数的图象交于点和点 , 点是点关于轴的对称点,连接 , .
(1)、用含 的代数式表示 的长;(2)、求 与 的函数表达式,并求当 随 增大而减小时 的取值范围.19. 如图,反比例函数与正比例函数的图象交于点和点 , 点是点关于轴的对称点,连接 , .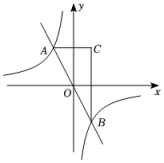 (1)、求该反比例函数的解析式;(2)、求的面积;(3)、请结合函数图象,直接写出不等式的解集.20. 如图1,灌溉车沿着平行于绿化带底部边线的方向行驶,为绿化带浇水,喷水口H离地竖直高度为 . 如图2,把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中两条抛物线的部分图象,把绿化带横截面抽象为矩形 , 其水平宽度 , 竖直高度为 . 下边缘抛物线是由上边缘抛物线向左平移得到,上边缘抛物线最高点A离喷水口的水平距离为 , 高出喷水口 , 喷出的水最远落在地面C处.
(1)、求该反比例函数的解析式;(2)、求的面积;(3)、请结合函数图象,直接写出不等式的解集.20. 如图1,灌溉车沿着平行于绿化带底部边线的方向行驶,为绿化带浇水,喷水口H离地竖直高度为 . 如图2,把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中两条抛物线的部分图象,把绿化带横截面抽象为矩形 , 其水平宽度 , 竖直高度为 . 下边缘抛物线是由上边缘抛物线向左平移得到,上边缘抛物线最高点A离喷水口的水平距离为 , 高出喷水口 , 喷出的水最远落在地面C处. (1)、求上边缘抛物线的函数解析式(用顶点式表示),并求喷出水的最大射程;(2)、灌溉车行驶时喷出的水能浇灌到整个绿化带,喷出的水恰好经过点F时,求此时点F的坐标.21. 某水产养殖户,一次性收购了小龙虾,计划养殖一段时间后再出售.已知每天放养的费用相同,放养天的总成本为万元;放养天的总成本为万元(总成本=放养总费用+收购成本).(1)、设每天的放养费用是a万元,收购成本为b万元,求a和b的值;(2)、设这批小龙虾放养t天后的质量为m(),销售单价为y元/.根据以往经验可知:m与t的函数关系式为 , y与t的函数关系如图所示
(1)、求上边缘抛物线的函数解析式(用顶点式表示),并求喷出水的最大射程;(2)、灌溉车行驶时喷出的水能浇灌到整个绿化带,喷出的水恰好经过点F时,求此时点F的坐标.21. 某水产养殖户,一次性收购了小龙虾,计划养殖一段时间后再出售.已知每天放养的费用相同,放养天的总成本为万元;放养天的总成本为万元(总成本=放养总费用+收购成本).(1)、设每天的放养费用是a万元,收购成本为b万元,求a和b的值;(2)、设这批小龙虾放养t天后的质量为m(),销售单价为y元/.根据以往经验可知:m与t的函数关系式为 , y与t的函数关系如图所示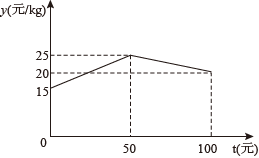
①求y与t的函数关系式;
②设将这批小龙虾放养t天后一次性出售所得利润为W元,求当t为何值时,W最大?并求出W的最大值.(利润=销售总额-总成本)
22. 已知:如图,抛物线与坐标轴分别交于点 , , , 点P是线段上方抛物线上的一个动点.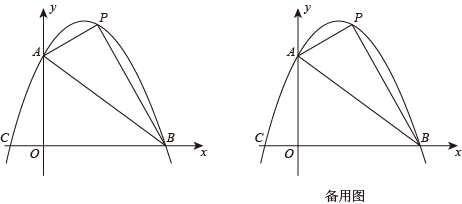 (1)、求抛物线的解析式;(2)、当点P运动到什么位置时,的面积有最大值,面积最大值是多少?(3)、已知抛物线的顶点为点D.点M是x轴上的一个动点,当点M的坐标为多少时,的周长最小?最小值是多少?
(1)、求抛物线的解析式;(2)、当点P运动到什么位置时,的面积有最大值,面积最大值是多少?(3)、已知抛物线的顶点为点D.点M是x轴上的一个动点,当点M的坐标为多少时,的周长最小?最小值是多少?