江苏省盐城市大丰区2022-2023学年七年级上学期期中数学试题

试卷更新日期：2022-12-19 类型：期中考试

进入出卷网下载

一、单选题

1. -1的相反数是（）

A、-1 B、0 C、1 D、2

查看试题解析
2. 多项式 $3 x^{2} - 2 x + 1$ 的各项分别是（）

A、3，2，1 B、 $x^{2}$ ， $x$ ， 1 C、 $3 x^{2}$ ， $2 x$ ， 1 D、 $3 x^{2}$ ， $- 2 x$ ， 1

查看试题解析
3. 2022年北京冬奥会计划于2月4日开幕.作为2022年北京冬奥会雪上项目的主要举办地，张家口市崇礼区建成7家大型滑雪场，拥有169条雪道，共162000米.数字162000用科学记数法表示为（）

A、 $162 \times 1 0^{3}$ B、 $16.2 \times 1 0^{4}$ C、 $1.62 \times 1 0^{5}$ D、 $0.162 \times 1 0^{6}$

查看试题解析
4. 单项式－2ab²的系数及次数分别是（）

A、0，2 B、一2，3 C、2，3 D、－2，2

查看试题解析
5. 当a为任意有理数时，下列代数式的值一定为正数的是（）

A、a B、 $a + 2$ C、2a D、 $a^{2} + 2$

查看试题解析
6. 单项式 $x^{m - 1} y^{3}$ 与 $- 4 x y^{n}$ 是同类项，则 $m^{n}$ 的值是（）

A、1 B、3 C、6 D、8

查看试题解析
7. 在﹣(﹣1)，﹣|﹣3.14|，0，(﹣3)⁴中，正数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 用“☆”定义一种新运算：对于任意有理数x和y，x☆y= $a^{2} x + a y + 1$ （a为常数），如：2☆3= $a^{2} \cdot 2 + a \cdot 3 + 1 = 2 a^{2} + 3 a + 1$ .若1☆2=3，则3☆6的值为（）

A、7 B、8 C、9 D、13

查看试题解析

二、填空题

9. 孔子出生于公元前551年，如果用-551来表示，则杜甫出生于公元712年表示为年.

查看试题解析
10. 比较大小：－4.3－3.4

查看试题解析
11. 数轴上与原点距离是4个单位长度的点所表示的数是 .

查看试题解析
12. 若关于x、y的多项式 $x^{2} - 2 k x y + y^{2} + 6 x y - 6$ 中不含xy项，则 $k =$ .

查看试题解析
13. 已知 $(x - 3)^{2} + | y + 5 | = 0$ ，则 $x + y =$

查看试题解析
14. 如图所示是计算机某计算程序，若开始输入x=2，则最后输出的结果是．

查看试题解析
15. 已知一个长为 $6 a$ ，宽为 $2 a$ 的长方形，如图1所示，沿图中虚线裁剪成四个相同的小长方形，按图2的方式拼接，则阴影部分正方形的边长是.(用含 $a$ 的代数式表示)

查看试题解析
16. 将一些相同的“〇”按如图所示的规律依次摆放，观察每个“龟图”的“〇”的个数，则第10个“龟图”中有个“〇”.

查看试题解析

三、解答题

17. 计算：

(1)、25-9+(-12)-(-7)；

(2)、 $\frac{1}{9} \times {(- 2)}^{3} \div {(\frac{2}{3})}^{2}$

查看试题解析
18. 计算题：

(1)、 $(\frac{5}{12} + \frac{2}{3} - \frac{3}{4}) \times (- 12)$ ；

(2)、 $- 1^{4} + (- 2) \div (- \frac{1}{3}) - | - 9 |$ .

查看试题解析
19. 已知一组数： $\frac{1}{2}$ ， 0 ，－3.5， 3， $- 2 \frac{1}{3}$ .

(1)、把这些数在下面的数轴上表示出来：

(2)、请将这些数按从小到大的顺序排列（用“＜”连接）.
.

查看试题解析
20. 把下列各数填入相应的括号内：
$- 6 ， - \frac{1}{6} ， 42 ， 0 ， - 0.33 ， - \frac{π}{3} ， 1 \frac{2}{5} ， - 3.3030030003 ⋯ ， - 2 . \dot{4} \dot{7}$
正数集合：（       …）
整数集合：（        …）
负分数集合：（        …）
无理数集合：（        …）

查看试题解析
21. 化简题：

(1)、 $3 x - y^{2} + x + y^{2}$ .

(2)、 $(5 a^{2} + 2 a - 1) - 4 (3 - 8 a + 2 a^{2})$ .

查看试题解析
22. 先化简，再求值：4（x²-2xy+3）-3（x²-xy+4），其中x＝-2，y＝ $\frac{1}{2}$ .

查看试题解析
23. 有8筐白菜，以每筐25千克为标准，超过的千克数记作正数，不足的千克数记作负数，称后的纪录如下：
编号
1
2
3
4
5
6
7
8
超过（或不足）
1.5
-3
2
-0.5
1
-2
-2.5
-2
回答下列问题：

(1)、这8筐白菜中最接近标准重量的这筐白菜重千克；

(2)、与标准重量比较，8筐白菜总计超过或不足多少千克？

(3)、若白菜每千克售价2.6元，则出售这8筐白菜可卖多少元？

查看试题解析
24. 盐外第18届运动会，初一某班需要购买运动鞋和短裤，运动鞋每双定价200元，短裤每条定价50元.某商店开展促销活动，可以同时向客户提供两种优惠方案：
方案一：买一双运动鞋送一条短裤；
方案二：运动鞋和短裤都按定价的90%付款.
现某班要购买运动鞋20双，短裤x条(x超过20).

(1)、若该班按方案一购买，需付款元；若该班按方案二购买，需付款元(用含x式子表示)；

(2)、当x=30时，哪种方案更划算？请通过计算说明理由；

(3)、若两种方案可以同时使用，当x=40时，你能给出一种最为省钱的购买方案吗？试写出你的购买方案，并计算该方案所需要付款金额.

查看试题解析
25. 我们用 $\bar{x y z}$ 表示一个三位数，其中x表示百位上的数，y表示十位上的数，z表示个位上的数，即 $\bar{x y z} = 100 x + 10 y + z$ .

(1)、说明 $\bar{a b c} + \bar{b c a} + \bar{c a b}$ 一定是111的倍数；

(2)、①写出一组a、b、c的取值，使 $\bar{a b c} + \bar{b c a} + \bar{c a b}$ 能被11整除，这组值可以是a= ， b= ， c=；
②若 $\bar{a b c} + \bar{b c a} + \bar{c a b}$ 能被11整除，则a、b、c三个数必须满足的数量关系是.

查看试题解析
26. 阅读：一个正整数n可以分解为两个正整数p、q的积，即 $n = p \times q$ （规定 $p \leq q$ ），在n的所有这种分解中，如果两因数p、q之差的绝对值最小，则称 $p \times q$ 是n的最优分解，称 $\frac{p}{q}$ 为n的最优分解比.

(1)、尝试：24可以分解成 $1 \times 24 、 2 \times 12 、 3 \times 8 、 4 \times 6$ ，其中 $4 \times 6$ 是24的最优分解，最优分解比为；

(2)、 $n^{2} - n$ 的最优分解是 $(n - 1) \times n$ ， $n^{2} - n$ 的最优分解比为；

(3)、请写出一个在20到40范围之间正整数：，使它的最优分解比为1；

(4)、探索：n是一个正整数（ $1 \leq n \leq 10 ）$ ，已知 $n^{2} - 2 n + 9$ 的最优分解比为 $\frac{1}{n^{2} - 2 n + 9}$ ，求 $n^{2} - 2 n + 9$ 的最小值，写出简要过程.

查看试题解析
27. 在数轴上有A、B两点，点B表示的数为b.对点A给出如下定义：当 $b \geq 0$ 时，将点A向右移动2个单位长度，得到点P；当 $b < 0$ 时，将点A向左移动 $| b |$ 个单位长度，得到点P.称点P为点A关于点B的“伴侣点”.如图，点A表示的数为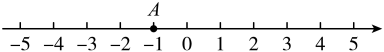 $- 1$ .

(1)、在图中画出当 $b = 6$ 时，点A关于点B的“伴侣点”P；

(2)、当点P表示的数为-6，若点P为点A关于点B的“伴侣点”，则点B表示的数；

(3)、点A从数轴上表示-1的位置出发，以每秒1个单位的速度向右运动，点B从数轴上表示8的位置同时出发，以每秒2个单位的速度向左运动，两个点运动的时间为t秒.
①点B表示的数为（用含t的式子表示）；

②是否存在t，使得此时点A关于点B的“伴侣点”P恰好与原点重合？若存在，请求出t的值；若不存在，请说明理由.

查看试题解析

编号	1	2	3	4	5	6	7	8
超过（或不足）	1.5	-3	2	-0.5	1	-2	-2.5	-2