江苏省盐城市大丰区2022-2023学年八年级上学期期中数学试题
试卷更新日期:2022-12-19 类型:期中考试
一、单选题
-
1. 下列常见的微信表情包中,属于轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 到三角形三个顶点距离相等的点是( )A、三边高线的交点 B、三条中线的交点 C、三边垂直平分线的交点 D、三条内角平分线的交点3. 下列各组数中,是勾股数的是( )A、6,8,10 B、4,6,8 C、0.3 ,0.4,0.5 D、3 ,6 ,94. 如图,在中,是斜边上的中线,若 , 则的度数为( )
2. 到三角形三个顶点距离相等的点是( )A、三边高线的交点 B、三条中线的交点 C、三边垂直平分线的交点 D、三条内角平分线的交点3. 下列各组数中,是勾股数的是( )A、6,8,10 B、4,6,8 C、0.3 ,0.4,0.5 D、3 ,6 ,94. 如图,在中,是斜边上的中线,若 , 则的度数为( ) A、 B、 C、 D、5. 的三条边分别为 , 下列条件不能判断是直角三角形的是( )A、 B、 C、 D、6. 用直尺和圆规作一个角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
A、 B、 C、 D、5. 的三条边分别为 , 下列条件不能判断是直角三角形的是( )A、 B、 C、 D、6. 用直尺和圆规作一个角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
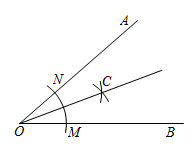 A、SSS B、ASA C、AAS D、SAS7. 如图,在等边中,D为BC边上的中点,以A为圆心,AD为半径画弧,与AC边交点为E,则的度数为( )
A、SSS B、ASA C、AAS D、SAS7. 如图,在等边中,D为BC边上的中点,以A为圆心,AD为半径画弧,与AC边交点为E,则的度数为( ) A、60° B、105° C、75° D、15°8. 在如图所示的网格中,是格点三角形(即顶点恰好是网格线的交点),则与有一条公共边且全等(不含)的所有格点三角形的个数是( )
A、60° B、105° C、75° D、15°8. 在如图所示的网格中,是格点三角形(即顶点恰好是网格线的交点),则与有一条公共边且全等(不含)的所有格点三角形的个数是( ) A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
9. 等腰三角形的顶角是100°,则底角是°.10. 小强站在镜前,从镜子中看到镜子对面墙上挂着的电子表,其读数如图所示,则电子表的实际时刻是.
 11. 如图,三个正方形围成一个直角三角形,64、400分别为所在正方形的面积,则图中字母M所代表的正方形面积是.
11. 如图,三个正方形围成一个直角三角形,64、400分别为所在正方形的面积,则图中字母M所代表的正方形面积是. 12. 如图,在中, , 是的垂直平分线,分别交于D、E两点.若 , 则的周长是.
12. 如图,在中, , 是的垂直平分线,分别交于D、E两点.若 , 则的周长是. 13. 如图,是直角三角形, , , cm.以点A为圆心、AB长为半径画弧,交BC边的延长线于点D,则AD长为cm.
13. 如图,是直角三角形, , , cm.以点A为圆心、AB长为半径画弧,交BC边的延长线于点D,则AD长为cm. 14. 如图,在正方形网格中,每个小正方形的边长都为 , 点在小正方形的格点上,连接 , 则.
14. 如图,在正方形网格中,每个小正方形的边长都为 , 点在小正方形的格点上,连接 , 则. 15. 如图,直线a,b交于点O,∠α=40°,点A是直线a上的一个定点,点B在直线b上运动,且始终位于直线a的上方,若以点O,A,B为顶点的三角形是等腰三角形,则∠OAB=°.
15. 如图,直线a,b交于点O,∠α=40°,点A是直线a上的一个定点,点B在直线b上运动,且始终位于直线a的上方,若以点O,A,B为顶点的三角形是等腰三角形,则∠OAB=°.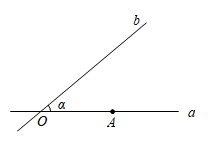 16. 如图,在中, , 点D为斜边的中点, , 连接 , 将△BCD沿翻折,使B落在点E处,点F为直角边上一点,连接 , 将沿翻折,使点A与点E重合,则的面积为.
16. 如图,在中, , 点D为斜边的中点, , 连接 , 将△BCD沿翻折,使B落在点E处,点F为直角边上一点,连接 , 将沿翻折,使点A与点E重合,则的面积为.
三、解答题
-
17. 如图,交于点O,在与中, , .求证:.
 18. 如图,△ABC中,已知AB=AC,BC平分∠ABD.
18. 如图,△ABC中,已知AB=AC,BC平分∠ABD. (1)、求证:;(2)、若∠A=100°,求∠1的度数.19. 已知:如图,在中, , 点D、E分别在边AC、AB上,且 , BD与CE相交于点O.求证:.
(1)、求证:;(2)、若∠A=100°,求∠1的度数.19. 已知:如图,在中, , 点D、E分别在边AC、AB上,且 , BD与CE相交于点O.求证:. 20. 已知:如图,AD∥BC,EF垂直平分BD,与AD,BC,BD分别交于点E,F,O.求证:
20. 已知:如图,AD∥BC,EF垂直平分BD,与AD,BC,BD分别交于点E,F,O.求证: (1)、△BOF≌△DOE;(2)、DE=DF.21. 如图,小旭放风筝时,风筝挂在了树上,他先拉住风筝线,垂直于地面,发现风筝线多出1米;把风筝线沿直线BC向后拉5米,风筝线末端刚好接触地面,求风筝距离地面的高度AB.
(1)、△BOF≌△DOE;(2)、DE=DF.21. 如图,小旭放风筝时,风筝挂在了树上,他先拉住风筝线,垂直于地面,发现风筝线多出1米;把风筝线沿直线BC向后拉5米,风筝线末端刚好接触地面,求风筝距离地面的高度AB. 22. 如图所示四边形 , 已知 , , , , , 求:
22. 如图所示四边形 , 已知 , , , , , 求: (1)、的长;(2)、该四边形的面积.23. 如图,的顶点均在正方形网格格点上,每个小正方形的边长为1.(作图只用不带刻度的直尺,不写作法,保留作图痕迹)
(1)、的长;(2)、该四边形的面积.23. 如图,的顶点均在正方形网格格点上,每个小正方形的边长为1.(作图只用不带刻度的直尺,不写作法,保留作图痕迹) (1)、试说明是等腰三角形;(2)、作出的角平分线;(3)、作出的边上的高.24. 中, , 过点A作 , 且 , 过点D作 于点E.
(1)、试说明是等腰三角形;(2)、作出的角平分线;(3)、作出的边上的高.24. 中, , 过点A作 , 且 , 过点D作 于点E. (1)、求证:;(2)、连接 , 若 , , 求的长.25. 如图,在Rt△ABC中, , , 动点P从B出发沿射线以1 cm/s的速度运动,设运动时间为t(s).
(1)、求证:;(2)、连接 , 若 , , 求的长.25. 如图,在Rt△ABC中, , , 动点P从B出发沿射线以1 cm/s的速度运动,设运动时间为t(s). (1)、求边的长.(2)、当为等腰三角形时,求t的值.26. 在四边形中,和有公共顶点O,且.
(1)、求边的长.(2)、当为等腰三角形时,求t的值.26. 在四边形中,和有公共顶点O,且. (1)、如图1,O是边上的一点.若.求证:.(2)、如图1,O是边上的一点.若 , 连接 , 交点为E,求的度数.(3)、如图2,B、O、C三点不在一条线上,且 , 满足 , 求的面积.27. 定义:一组对角互补,且对角线平分其中一个内角,称四边形为余缺四边形.
(1)、如图1,O是边上的一点.若.求证:.(2)、如图1,O是边上的一点.若 , 连接 , 交点为E,求的度数.(3)、如图2,B、O、C三点不在一条线上,且 , 满足 , 求的面积.27. 定义:一组对角互补,且对角线平分其中一个内角,称四边形为余缺四边形.如图1,四边形 , , 平分 , 则四边形为余缺四边形.
 (1)、【概念理解】
(1)、【概念理解】
用(填序号)一定可以拼成余缺四边形.①两个全等的直角三角形, ②两个全等的等边三角形;
(2)、如图1,余缺四边形 , 平分 , 若 , , 则;(3)、【初步应用】如图2,已知△ABC,∠BAC的平分线AP与BC的垂直平分线交于P点,连接PB、PC.
求证:四边形ABPC为余缺四边形; (4)、若 , , 则的值为.(5)、【迁移应用】
(4)、若 , , 则的值为.(5)、【迁移应用】
如图3, , 等腰的B、C两点分别在射线上,且斜边 (P、A在两侧),若B、C两点在射线、上滑动时,四边形的面积是否发生变化?若不变化,请说明理由;若变化,直接写出面积的最大的值.