江苏省徐州市丰县2021-2022学年九年级上学期期中数学试题
试卷更新日期:2022-12-19 类型:期中考试
一、单选题
-
1. 将一元二次方程 化为一般形式后,其中二次项系数、一次项系数分别是( )A、 B、 C、 D、2. 已知关于 的方程 的一个根是-1,则 的值是( )A、-2 B、-1 C、1 D、23. 是 的外接圆,则点 是 的( )A、三条边的垂直平分线的交点 B、三条角平分线的交点 C、三条中线的交点 D、三条高的交点4. 如图,正六边形内接于.连接.则的度数是( )
 A、 B、 C、 D、5. 如图,⊙O的半径为5,弦AB=8,P是弦AB上的一个动点(不与A、B重合),下列符合条件的OP的值是( )
A、 B、 C、 D、5. 如图,⊙O的半径为5,弦AB=8,P是弦AB上的一个动点(不与A、B重合),下列符合条件的OP的值是( ) A、5.8 B、3.8 C、1.3 D、2.56. 如图,⊙O是△ABC的内切圆,若∠A=70°,则∠BOC=( )
A、5.8 B、3.8 C、1.3 D、2.56. 如图,⊙O是△ABC的内切圆,若∠A=70°,则∠BOC=( ) A、125° B、115° C、100° D、130°7. 将抛物线先向下平移4个单位,再向左平移5个单位,得到的新抛物线的函数关系式为( )A、 B、 C、 D、8. 二次函数y=ax2+bx+c的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为( ,﹣2);⑤当x< 时,y随x的增大而减小;⑥a+b+c>0正确的有( )
A、125° B、115° C、100° D、130°7. 将抛物线先向下平移4个单位,再向左平移5个单位,得到的新抛物线的函数关系式为( )A、 B、 C、 D、8. 二次函数y=ax2+bx+c的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为( ,﹣2);⑤当x< 时,y随x的增大而减小;⑥a+b+c>0正确的有( )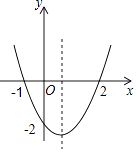 A、3个 B、4个 C、5个 D、6个
A、3个 B、4个 C、5个 D、6个二、填空题
-
9. 的半径为4,圆心O到直线l的距离为2,则直线l与的位置关系是.10. 如图,在⊙O内接四边形 中,若 ,则 .
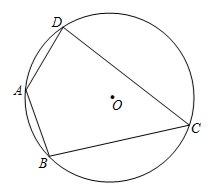 11. 如图, 是 的直径,点 在 上,若 ,则 °.
11. 如图, 是 的直径,点 在 上,若 ,则 °. 12. 若一元二次方程 有两个不相等的实数根,则c的值可以是(写出一个即可).13. 把二次三项式 化成 的形式应为.14. 二次函数图像的对称轴是.15. 如图所示,在建筑工地上,为了支撑一堵墙,用一根长为5m的木材,顶端撑在墙上,底端撑在地面上, , 现为了增加支撑效果,底端向前移动m,问:顶端需上移多少米?在这个问题中,设顶端上移x米,则可列方程为.
12. 若一元二次方程 有两个不相等的实数根,则c的值可以是(写出一个即可).13. 把二次三项式 化成 的形式应为.14. 二次函数图像的对称轴是.15. 如图所示,在建筑工地上,为了支撑一堵墙,用一根长为5m的木材,顶端撑在墙上,底端撑在地面上, , 现为了增加支撑效果,底端向前移动m,问:顶端需上移多少米?在这个问题中,设顶端上移x米,则可列方程为. 16. 如图,为的切线,点A为切点,交于点C,点D在上,连接、 , , 若 , 则的度数为°.
16. 如图,为的切线,点A为切点,交于点C,点D在上,连接、 , , 若 , 则的度数为°. 17. 如图,抛物线y=ax2+bx与直线y=kx相交于O , A(3,2)两点,则不等式ax2+bx﹣kx<0的解集是 .
17. 如图,抛物线y=ax2+bx与直线y=kx相交于O , A(3,2)两点,则不等式ax2+bx﹣kx<0的解集是 . 18. 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,D是以点A为圆心2为半径的圆上一点,连接BD,M为BD的中点,则线段CM长度的最小值为.
18. 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,D是以点A为圆心2为半径的圆上一点,连接BD,M为BD的中点,则线段CM长度的最小值为.
三、解答题
-
19. 解方程:(1)、;(2)、.20. 若关于x的方程有两个相等的实数根(1)、求b的值;(2)、当b取正数时,求此时方程的根,21. 下表给出一个二次函数的一些取值情况:
x
⋯
0
1
2
3
4
⋯
y
⋯
3
0
0
n
⋯
(1)、n= , 二次函数表达式为;(2)、请在直角坐标系中画出这个二次函数的图象; (3)、根据图像说明:当x取何值时,y的值为非负数?22. 如图,在两个同心圆O中,、都是大圆的弦,且 , 与小圆相切于点D,则与小圆相切吗?请说明理由.
(3)、根据图像说明:当x取何值时,y的值为非负数?22. 如图,在两个同心圆O中,、都是大圆的弦,且 , 与小圆相切于点D,则与小圆相切吗?请说明理由.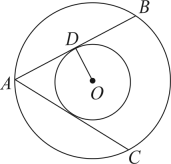 23. 已知,如图,扇形AOB的圆心角为120°,半径OA为6cm.
23. 已知,如图,扇形AOB的圆心角为120°,半径OA为6cm. (1)、求扇形AOB的弧长和扇形面积;(2)、若把扇形纸片AOB卷成一个圆锥无底纸盒,求这个纸盒的高OH.24. 某市场销售一批名牌衬衫,平均每天可销售20件,每件赢利40元.为了扩大销售,增加赢利,尽快减少库存,商场决定采取适当降价措施.经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.求:(1)、若商场平均每天赢利1200元,且让顾客得到实惠,每件衬衫应降价多少元?(2)、要使商场平均每天赢利最多,请你帮助设计方案.
(1)、求扇形AOB的弧长和扇形面积;(2)、若把扇形纸片AOB卷成一个圆锥无底纸盒,求这个纸盒的高OH.24. 某市场销售一批名牌衬衫,平均每天可销售20件,每件赢利40元.为了扩大销售,增加赢利,尽快减少库存,商场决定采取适当降价措施.经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.求:(1)、若商场平均每天赢利1200元,且让顾客得到实惠,每件衬衫应降价多少元?(2)、要使商场平均每天赢利最多,请你帮助设计方案.
25. 阿基米德折弦定理:如图1,和是的两条弦(即折线是圆的一条折弦), , M是的中点,则从M向所作垂线的垂足D是折弦的中点,即.下面是运用“截长法”证明的部分证明过程.
证明:如图2,在上截取 , 连接和.
∵M是的中点,
∴
任务:
 (1)、请按照上面的证明思路,写出该证明的剩余部分;(2)、填空:如图(3),已知等边内接于 , , D为上 一点, , 与点E,则的周长是.26. 如图,抛物线的图像经过点 , , 直线经过点A,交抛物线于点D.
(1)、请按照上面的证明思路,写出该证明的剩余部分;(2)、填空:如图(3),已知等边内接于 , , D为上 一点, , 与点E,则的周长是.26. 如图,抛物线的图像经过点 , , 直线经过点A,交抛物线于点D. (1)、求抛物线的函数关系式;(2)、若点E在线段上,连接且满足 , 点G是抛物线顶点,连接、 , 请你把图形补充完整,判断四边形的形状,并说明理由.
(1)、求抛物线的函数关系式;(2)、若点E在线段上,连接且满足 , 点G是抛物线顶点,连接、 , 请你把图形补充完整,判断四边形的形状,并说明理由.