湖北省荆门市京山市2022-2023学年九年级上学期期中教学质量监测数学试题

试卷更新日期：2022-12-19 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图形中，不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 一元二次方程 $x^{2}$ -8x-1=0配方后可变形为（　　）

A、 $(x + 4)^{2}$ =17 B、 $(x + 4)^{2}$ =15 C、 $(x - 4)^{2}$ =17 D、 $(x - 4)^{2}$ =15

查看试题解析
3. “圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题，“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何?”用现在的数学语言表述是：如图所示，CD为⊙O的直径，弦AB⊥CD，垂足为E，CE为1寸，AB为10寸，求直径CD的长.依题意，CD长为（）

A、 $\frac{25}{2}$ 寸 B、13寸 C、25寸 D、26寸

查看试题解析
4. 抛物线 $y = {(x - 3)}^{2} - 2$ 经过平移得到抛物线 $y = x^{2}$ ，平移过程正确的是（）

A、先向下平移2个单位，再向左平移3个单位 B、先向上平移2个单位，再向右平移3个单位 C、先向下平移2个单位，再向右平移3个单位 D、先向上平移2个单位，再向左平移3个单位.

查看试题解析
5. 我区高效课堂建设确定以“信息技术与课堂教学深度融合”为抓手，加强对教师队伍建设的投入，计划从2020年起三年共投入3640万元，已知2020年投入1000万元，设投入经费的年平均增长率为 $x$ ，根据题意，下面所列方程正确的是（）

A、 $1000 {(1 + x)}^{2} = 3640$ B、 $1000 + 1000 x + 1000 x^{2} = 3640$ C、 $1000 (1 + x^{2}) = 3640$ D、 $1000 (1 + x) + 1000 {(1 + x)}^{2} = 2640$

查看试题解析
6. 在同一坐标系中，一次函数 $y = a x + c$ 与二次函数 $y = a x^{2} + c$ 的图象可能是（）

A、 B、 C、 D、

查看试题解析
7.
如图，在Rt△ABC中，∠BAC=90°，将△ABC绕点A顺时针旋转90°后得到的△AB′C′（点B的对应点是点B′，点C的对应点是点C′），连接CC′．若∠CC′B′=32°，则∠B的大小是（　　）

A、32° B、64° C、77° D、87°

查看试题解析
8. 如果关于x的一元二次方程 ${kx}^{2} - \sqrt{2k + 1} x + 1 = 0$ 有两个不相等的实数根，那么k的取值范围是（）

A、k＜ $\frac{1}{2}$ B、k＜ $\frac{1}{2}$ 且k≠0 C、﹣ $\frac{1}{2}$ ≤k＜ $\frac{1}{2}$ D、﹣ $\frac{1}{2}$ ≤k＜ $\frac{1}{2}$ 且k≠0

查看试题解析
9. 已知二次函数y＝ax²－2ax＋1（a为常数，且a＞0）的图象上有三点A（－2，y₁），B（1，y₂），C（3，y₃），则y₁ ， y₂ ， y₃的大小关系是（）

A、y₁＜y₂＜y₃ B、y₁＜y₃＜y₂ C、y₂＜y₁＜y₃ D、y₂＜y₃＜y₁

查看试题解析
10. 如果m、n是一元二次方程x²+x＝4的两个实数根，那么多项式2n²-mn-2m的值是（　　）

A、16 B、14 C、10 D、6

查看试题解析

二、填空题

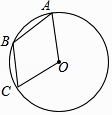
11. 已知一元二次方程x²－c＝0有一个根为2，则c的值为.

查看试题解析
12. 在平面直角坐标系中，点（3，-2）关于原点对称的点的坐标是．

查看试题解析
13. 某种植物的主干长出若干数目的枝干，每个枝干又长出同样数目的小分支，主干、支干和小分支的总数是91，那么每个支干长出小分支.

查看试题解析
14. 抛物线y＝ax²+bx+c经过点A（-1，0）、B（5，0）两点，则关于x的一元二次方程a（x-1）²＝b-bx的解是.

查看试题解析
15. 如图，A、B、C是⊙O上的三点，且四边形OABC是菱形．若点D是圆上异于A、B、C的另一点，则∠ADC的度数是．

查看试题解析
16. 下列关于二次函数 $y = x^{2} - 2 m x + 1$ （m为常数）的结论：
①该函数的图象与函数 $y = - x^{2} + 2 m x$ 的图象的对称轴相同；

②该函数的图象与x轴有交点时，m＞1；

③该函数的图象的顶点在函数 $y = - x^{2} + 1$ 的图象上；

④点A（ $x_{1} ， y_{1}$ ）与点B（ $x_{2} ， y_{2}$ ）在该函数的图象上.若 $x_{1} < x_{2}$ ， $x_{1} + x_{2} < 2 m$ ，则 $y_{1} < y_{2}$ .

其中正确的结论是（填写序号）.

查看试题解析

三、解答题

17. 解下列方程：

(1)、x²-8x-1=0；

(2)、 $x (2 x - 5) = 4 x - 10$

查看试题解析
18. 如图，将△ABC绕点C顺时针旋转得到△DEC，点D落在线段AB上.求证：DC平分∠ADE.

查看试题解析
19. 如图，要设计一本书的封面，封面长40cm，宽30cm，正中央是一个与整个封面长宽比例相同的矩形，如果要使四周边衬所占面积是封面面积的 $\frac{7}{16}$ ，且上、下边衬等宽，左、右边衬等宽，求上下边衬的宽.

查看试题解析
20. 如图，利用函数 $y = x^{2} - 4 x + 3$ 的图象，直接回答：

(1)、方程 $x^{2} - 4 x + 3 = 0$ 的解是；

(2)、当x时，y随x的增大而减小；

(3)、当x满足时，函数值大于0；

(4)、当 $0 < x < 5$ 时，y的取值范围是.

查看试题解析
21. 已知关于x的方程x²+（2k﹣1）x+k²﹣1=0有两个实数根x₁ ， x₂ ．

(1)、求实数k的取值范围；

(2)、若x₁ ， x₂满足x₁²+x₂²=16+x₁x₂ ，求实数k的值．

查看试题解析
22. 如图，A、P、B、C是 $⊙ O$ 上的四个点， $∠ A P C = ∠ C P B = 60 °$ .

(1)、判断 $△ A B C$ 的形状，并证明你的结论；

(2)、探究 $P A$ 、 $P B$ 、 $P C$ 之间的数量关系，并证明你的结论.

查看试题解析
23. 某宾馆有50个房间供游客住宿，当每个房间的房价为每天180元时，房间会全部住满．当每个房间每天的房价每增加10元时，就会有一个房间空闲．宾馆需对游客居住的每个房间每天支出20元的各种费用．根据规定，每个房间每天的房价不得高于340元．设每个房间的房价每天增加x元（x为10的整数倍）．

(1)、设一天订住的房间数为y，直接写出y与x的函数关系式及自变量x的取值范围；

(2)、设宾馆一天的利润为w元，求w与x的函数关系式；

(3)、一天订住多少个房间时，宾馆的利润最大？最大利润是多少元？

查看试题解析
24. 已知抛物线 $y = a x^{2} - 3 a x - 4 a$ 与x轴交于 $A 、 B$ 两点（A左B右），交y轴负半轴点C，P是第四象限抛物线上一点．

(1)、若 $S_{△ A B C} = 5$ ，求a的值；

(2)、若 $a = 1$ ，过点P作直线垂直于x轴，交 $B C$ 于点Q，求线段 $P Q$ 的最大值，并求此时点P的坐标；

(3)、直线 $A P$ 交y轴于点M，直线 $B P$ 交y轴于点N，求 $\frac{4 O M + O N}{O C}$ 的值．

查看试题解析