湖北省荆门市京山市2022-2023学年八年级上学期期中教学质量监测数学试题

试卷更新日期：2022-12-19 类型：期中考试

进入出卷网下载

一、单选题

1. 下列长度的三条线段可以组成三角形的是（　　）

A、2，3，4 B、5，6，12 C、1，5，9 D、2，5，7

查看试题解析
2. 在平面直角坐标系中，点 $A (1, - 2)$ 关于x轴对称的点的坐标为（）

A、 $(1, 2)$ B、 $(- 1, 2)$ C、 $(2, 1)$ D、 $(- 1, - 2)$

查看试题解析
3. 下面作三角形最长边上的高正确的是（）

A、 B、 C、 D、

查看试题解析
4. 若一个多边形的内角和小于其外角和,则这个多边形的边数是（）

A、3 B、4 C、5 D、6

查看试题解析
5. 用三角尺可按下面方法画角的平分线.如图，在 $∠ A O B$ 两边上，分别取 $O M ＝ O N$ ，再分别过点M，N作 $O A$ ， $O B$ 的垂线，交点为P，画射线 $O P$ ，可得 $△ P O M ≌ △ P O N$ .则判定三角形全等的依据是（）

A、 $S S S$ B、 $S A S$ C、 $A S A$ D、 $H L$

查看试题解析
6. 如图，在 $△ A B C$ 中，D，E分别是边 $A C$ ， $B C$ 上的点，若 $△ A D B ≌ △ E D B ≌ △ E D C$ ，则 $∠ C$ 的度数为（）

A、 $15 °$ B、 $20 °$ C、 $25 °$ D、 $30 °$

查看试题解析
7. 下列条件不能判定两个直角三角形全等的是（）

A、两条直角边对应相等 B、斜边和一锐角对应相等 C、斜边和一直角边对应相等 D、两个直角三角形的面积相等

查看试题解析
8. 如图， $△ A B C$ 中 $B C$ 边上的高为 $h_{1} ， △ D E F$ 中 $D E$ 边上的高为 $h_{2}$ ，下列结论正确的是（）

A、 $h_{1} > h_{2}$ B、 $h_{1} < h_{2}$ C、 $h_{1} = h_{2}$ D、无法确定

查看试题解析
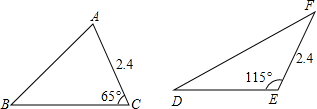9. 如图，在△ABC中，AB=AC，D、E是△ABC内的两点，AD平分∠BAC，∠EBC=∠E=60°，若BE=10cm，DE=4cm，则BC的长为（）

A、7cm B、12cm C、14cm D、16cm

查看试题解析
10. 如图，在 $3 \times 3$ 的正方形的网格中，格线的交点称为格点，以格点为顶点的三角形称为格点三角形，图中的 $△ A B C$ 为格点三角形，在图中最多能画出（）个格点三角形与 $△ A B C$ 成轴对称.

A、6 B、5 C、4 D、3

查看试题解析

二、填空题

11. 木工师傅在做好门框后，为了防止变形常常按如图那样钉上两根斜拉的木板条，即图中的 $A B$ 、 $C D$ 两根木条，其数学依据是.

查看试题解析
12. 在测量一个小口圆形容器的壁厚时，小明用“x型转动钳”按如图方法进行测量，其中 $O A = O D ， O B = O C$ ，测得 $A B = 5 c m ， E F = 7 c m$ ，圆形容器的壁厚是 $c m$ .

查看试题解析
13. 如图，在等腰 $△ A B C$ 中， $A B = A C$ ， $A B$ 的垂直平分线 $M N$ 分别与 $A B$ 、 $A C$ 交于E、D两点.若 $B E = 5$ ， $B C = 8$ ，则 $△ B C D$ 的周长是.

查看试题解析
14. 如图， $A B ⊥ C D$ ，且 $A B = C D$ ， $C E ⊥ A D$ 于E， $B F ⊥ A D$ 于F.若 $C E = 6$ ， $B F = 3$ ， $E F = 2$ ，则 $A D$ 的长为.

查看试题解析
15. 如图，在 $△ A B C$ 和 $△ D E C$ 中， $A B ＝ D E$ ， $A C ＝ D C$ ， $C E ＝ C B$ .点E在 $A B$ 上，若 $∠ A C E ＝ 2 ∠ E C B ＝ 50 °$ ，则 $∠ A$ ＝.

查看试题解析
16. 如图，已知 $△ A B C$ 和 $△ C D E$ 都是等边三角形，点 $B 、 C 、 D$ 在同一条直线上， $B E$ 交 $A C$ 于M， $A D$ 交 $C E$ 于N， $A D 、 B E$ 交点O；下列说法：① $A D = B E$ ；② $△ M N C$ 为等边三角形；③ $∠ B O D = 110 °$ ；④ $C O$ 平分∠ $B O D$ .其中一定正确的是（只需填写序号）.

查看试题解析

三、解答题

17. 如图，B，E，C，F在一条直线上， $A B ＝ D E$ ， $A C ＝ D F$ ， $B E ＝ C F$ ，求证： $∠ A ＝ ∠ D$ .

查看试题解析
18. 如图，在 $△ A B C$ 中，∠B=25°，∠BAC=31°，过点A作BC边上的高，交BC的延长线于点D ， CE平分∠ACD ，交AD于点E ．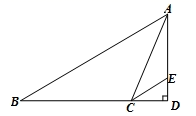
求：

(1)、∠ACD的度数；

(2)、∠AEC的度数．

查看试题解析
19. 用一条长为 $18 cm$ 的细绳围成一个等腰三角形.

(1)、如果腰长是底边长的2倍，那么各边的长是多少？

(2)、能围成有一边长是 $4 cm$ 的等腰三角形吗？为什么？

查看试题解析
20. 如图， $△ A B C$ 的顶点A、B、C都在小正方形的顶点上，试在方格纸上按下列要求画格点三角形（三角形的顶点在格点上），只需画出一个即可：

(1)、在图（1）中画出与 $△ A B C$ 全等的三角形，且有条公共边：

(2)、在图（2）中画出与 $△ A B C$ 全等的三角形，且有一个公共顶点：

(3)、在图（3）中画出与 $△ A B C$ 全等的三角形，且有一个公共角.

查看试题解析
21. 如图，点D，E在△ABC的边BC上，AB=AC，AD=AE.

(1)、求证：BD=CE；

(2)、若AD=BD=DE，求∠BAC的度数.

查看试题解析
22. 已知 $△ A B C$ 中， $B C ＝ A B$ ， $∠ A B C ＝ 90 °$ ， A点在x负半轴上，直角顶点B在y轴上，点C在x轴上方.

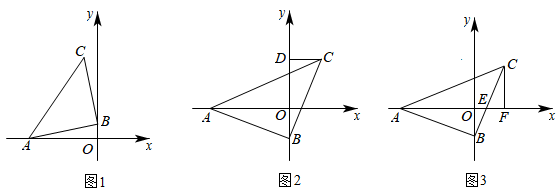(1)、如图1所示，若A的坐标是（ $- 3$ ， 0），点B的坐标是（0，1），求点C的坐标；

(2)、如图2，过点C作 $C D ⊥ y$ 轴于D，求证： $O A ＝ C D + O D$ ；

(3)、如图3，若x轴恰好平分 $∠ B A C$ ， $B C$ 与x轴交于点E，过点C作 $C F ⊥ x$ 轴于F，求证： $C F ＝ \frac{1}{2} A E$ .

查看试题解析
23.

(1)、如图①，在 $△ A B C$ 中， $∠ A B C$ 的平分线 $B O$ 与 $∠ A C B$ 的平分线 $C O$ 交于点O，求证： $∠ B O C = 9 0^{°} + \frac{1}{2} ∠ A ；$

(2)、如图②，在 $△ A B C$ 中， E是边BC延长线上一点， $∠ A B C$ 的平分线 $B O$ 与 $∠ A C E$ 的平分线 $C O$ 交于点O，求证： $∠ B O C = \frac{1}{2} ∠ A$ ；

(3)、如图③，在 $△ A B C$ 中，D是边 $A B$ 延长线上一点，E是边 $A C$ 延长线上一点， $∠ C B D$ 的平分线 $B O$ 与 $∠ B C E$ 的平分线 $C O$ 交于点O.
①试探求∠A与 $∠ B O C$ 的数量关系并证明你的结论；
②按角的大小来判断 $△ B O C$ 的形状.

查看试题解析
24. 如图1， $△ A B C$ 中， $A B = A C$ ，点D在AB上，且 $A D = C D = B C$ .

(1)、求 $∠ A$ 的大小；

(2)、如图2， $D E ⊥ A C$ 于E， $D F ⊥ B C$ 于F，连接EF交CD于点H.
①求证：CD垂直平分EF：
②猜想三条线段AE，DB，BF之间的数量关系，并对你的猜想进行说明.

查看试题解析