河南省驻马店市泌阳县2022-2023学年八年级上学期期中数学试卷

试卷更新日期：2022-12-19 类型：期中考试

进入出卷网下载

一、单选题

1. 在实数 $\sqrt{7}$ ， $\sqrt{\frac{1}{8}}$ ， $- \sqrt{16}$ ， $\frac{π}{2}$ ， $\sqrt[3]{9}$ ， $1.010010001$ ， $\frac{22}{7}$ 中，无理数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 下列式子运算正确的是（）

A、 $a^{8} \div a^{2} = a^{6}$ B、 $a^{2} + a^{3} = a^{5}$ C、 ${(a + 1)}^{2} = a^{2} + 1$ D、 $3 a^{2} - 2 a^{2} = 1$

查看试题解析
3. 一个正数的两个平方根分别为 $2 m - 1$ 与 $2 - m$ ，则m的值为（）

A、1 B、2 C、 $- 1$ D、 $- 2$

查看试题解析
4. 计算 ${(\frac{2}{3})}^{2020} \times {(\frac{3}{2})}^{2021}$ 的结果是（）

A、 $\frac{2}{3}$ B、 $- \frac{2}{3}$ C、 $\frac{3}{2}$ D、 $- \frac{3}{2}$

查看试题解析
5. 若 $a + b = 2$ ，则 $a^{2} - b^{2} + 4 b$ 的值为（）

A、2 B、3 C、4 D、6

查看试题解析
6. 如图，已知 $A B = A C ， A B = 5 ， B C = 3$ ，以 $A B$ 两点为圆心，大于 $\frac{1}{2} A B$ 的长为半径画圆，两弧相交于点 $M ， N$ ，连接 $M N$ 与 $A C$ 相较于点 $D$ ，则 $Δ B D C$ 的周长为（）

A、8 B、10 C、11 D、13

查看试题解析
7. 如（x+m）与（x+3）的乘积中不含x的一次项，则m的值为（）

A、 $- 3$ B、3 C、0 D、1

查看试题解析
8. 下列命题是假命题的有（　　）.
①若a²＝b² ，则a＝b；②一个角的余角大于这个角；③若a，b是有理数，则|a＋b|＝|a|＋|b|；④如果∠A＝∠B，那∠A与∠B是对顶角.

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 如图，在Rt△ABC中， $∠ A C B = 90 °$ ， $B C = 4 c m$ ，在AC上取一点E，使 $E C = B C$ ，过点E作 $E F ⊥ A C$ ，连接CF，使 $C F = A B$ ，若 $E F = 10 c m$ ，则AE的长为（）

A、5cm B、6cm C、7cm D、无法计算

查看试题解析
10. 如图，AB//DE，AC//DF，AC＝DF，下列条件中，不能判定△ABC≌△DEF的是（）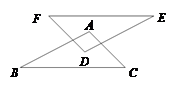

A、AB＝DE B、∠B＝∠E C、EF＝BC D、EF//BC

查看试题解析

二、填空题

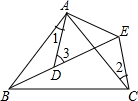
11. $\sqrt{81}$ 的算术平方根是

查看试题解析
12. 已知a＋ $\frac{1}{a}$ ＝5，则a²＋ $\frac{1}{a^{2}}$ 的结果是．

查看试题解析
13. 若多项式 $x^{2} ＋ 2 (m - 2) x ＋ 25$ 能用完全平方公式因式分解，则m的值为．

查看试题解析
14. 三角形的三边a，b，c满足 $\sqrt{a - b}$ +(b-c)²＝0；则三角形是三角形.

查看试题解析
15. 如图所示，AB＝AC ， AD＝AE ， ∠BAC＝∠DAE ， ∠1＝25°，∠2＝30°，则∠3＝．

查看试题解析
16. 如图，DE⊥AB于E，DF⊥AC于F，若BD＝CD，BE＝CF，则下列结论：①DE＝DF；②AD平分∠BAC；③AE＝AD；④AC﹣AB＝2BE中正确的是．

查看试题解析

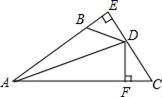
三、解答题

17. 计算下列各题

(1)、 ${(- 2)}^{3} + \sqrt{{(- 4)}^{2}} - \sqrt[3]{- 8} \times \sqrt{\frac{1}{4}}$

(2)、 $9 {(a - 1)}^{2} - (3 a + 2) (3 a - 1)$

(3)、 $[{(x + y)}^{2} - {(x - y)}^{2}] \div 2 x y$

查看试题解析
18. 因式分解：

(1)、 ${(a + b)}^{2} + 10 (a + b) + 25$ ；

(2)、 $x^{3} - 9 x$ .

查看试题解析
19. 先化简，再求值， ${(x - y)}^{2} + (3 x - y) (x + y) - (x - 2 y) (x + 2 y)$ ，其中x，y满足 ${(x + 2)}^{2} + | y - 3 | = 0$ .

查看试题解析
20. 已知一个正数m的两个不相等的平方根是a+6与2a-9．

(1)、求a和m的值；

(2)、求关于x的方程 $a x^{2} - 16 = 0$ 的解．

查看试题解析
21. 如图，幼儿园有两个长度相同的滑梯，左边滑梯的高度 $A C$ 与右边滑梯水平方向的长度 $D F$ 相等，

(1)、 $Δ A B C ≌ Δ D E F$ 吗？

(2)、两个滑梯的倾斜角 $∠ A B C$ 和 $∠ D F E$ 有什么关系？

查看试题解析
22. 阅读材料：如果一个三角形的三边长分别为a，b，c，记 $p = \frac{a + b + c}{2}$ ，那么这个三角形的面积为 $S = \sqrt{p (p - a) (p - b) (p - c)}$ .这个公式叫“海伦公式”，它是利用三角形的三条边的边长直接求三角形面积的公式，中国秦九韶也得出了类似的公式，称三斜求积术，故这个公式又被称为“海伦——秦九韶公式”.完成以下问题：如图，在 $△$ $A B C$ 中， $a = 5$ ， $b = 3$ ， $c = 4$ .

(1)、求 $△$ $A B C$ 的面积；

(2)、过点A作 $A D ⊥ B C$ ，垂足为D，求线段 $A D$ 的长.

查看试题解析
23. 如图，将一张长方形纸板按图中虚线裁剪成九块，其中有两块是边长都为m的大正方形，两块是边长都为n的小正方形，五块是长为m，宽为n的全等小长方形，且m>n.(以上长度单位：cm)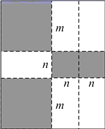

(1)、观察图形，可以发现代数式2m²＋5mn＋2n²可以因式分解为；

(2)、若每块小长方形的面积为10 cm² ，四个正方形的面积和为58 cm² ，试求图中所有裁剪线(虚线部分)长之和.

查看试题解析
24. 如图，在△ABC中，∠B＝60°，AD平分∠BAC，CE平分∠BCA，AD、CE交于点F，CD＝CG，连结FG.

(1)、求证：FD＝FG；

(2)、线段FG与FE之间有怎样的数量关系，请说明理由；

(3)、若∠B≠60°，其他条件不变，则（1）和（2）中的结论是否仍然成立？请直接写出判断结果，不必说明理由.

查看试题解析