河南省省直辖县级行政单位2022-2023学年九年级上学期期中数学试题

试卷更新日期：2022-12-19 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图案中不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若关于x的方程（m-3）x^|m^-^1|+5x-3＝0是一元二次方程，则m的值为（　　）

A、3 B、-1 C、3或-1 D、0

查看试题解析
3. 用配方法解方程 $x^{2} + 2 x - 5 = 0$ 时，原方程应变形为（　　）

A、 ${(x + 1)}^{2} = 6$ B、 ${(x - 1)}^{2} = 6$ C、 ${(x + 2)}^{2} = 9$ D、 ${(x - 2)}^{2} = 9$

查看试题解析
4. 将抛物线y＝2（x-1）²-3先向上平移2个单位长度，再向左平移3个单位长度，得到的抛物线的解析式为（　　）

A、y＝2（x+2）²-1 B、y＝2（x+2）²-5 C、y＝2（x-4）²-1 D、y＝2（x-4）²-5

查看试题解析
5. 关于x一元二次方程 $(a - 1) x^{2} + x + a^{2} - 1 = 0$ 的一个根是0，则a的值为（）

A、1或 $- 1$ B、1 C、 $- 1$ D、0

查看试题解析
6. 根据下列表格对应值，判断关于 $x$ 的方程 $a x^{2} + b x + c = 3$ 的一个解 $x$ 的范围是（）
$x$
1.1
1.2
1.3
1.4
$a x^{2} + b x + c$
-0.59
0.84
2.29
3.76

A、1.1＜x＜1.2 B、1.2＜x＜1.3 C、1.3＜x＜1.4 D、无法判定

查看试题解析
7. 如图，在Rt $△$ ABC中，∠ACB＝90°，将Rt $△$ ABC绕点C顺时针方向旋转一定角度得到Rt $△$ DEC ，点D恰好落在边AB上．若∠B＝25°，则∠BCE的度数为（　　）

A、20° B、30° C、50° D、60°

查看试题解析
8. 某机械厂七月份生产零件50万个，第三季度生产零件196万个．设该厂八、九月份平均每月的增长率为x，那么x满足的方程是（）

A、50（1+x²）=196 B、50+50（1+x²）=196 C、50+50（1+x）+50（1+x）²=196 D、50+50（1+x）+50（1+2x）=196

查看试题解析
9. 已知二次函数 $y = a x^{2} + b x + c$ 图象的对称轴为 $x = 1$ ，其图象如图所示，现有下列结论：① $a b c > 0$ ；② $b - 2 a < 0$ ；③ $a - b + c > 0$ ；④ $a + b > n (a n + b) ， (n \neq 1)$ ；⑤ $2 c < 3 b$ ．正确的是（）

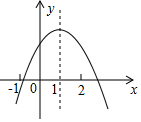A、①③ B、②⑤ C、③④ D、④⑤

查看试题解析
10. 如图，将△ABC绕点C（0，-1）旋转180°得到△A′B′C，设点A的坐标为（a，b），则点A′的坐标为（）

A、（-a，-b） B、（-a，-b-1） C、（-a，-b+1） D、（-a，-b-2）

查看试题解析

二、填空题

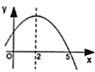
11. 已知一个二次函数的图象开口向上，顶点坐标为（0，﹣1 ），那么这个二次函数的解析式可以是．（只需写一个）

查看试题解析
12. 已知点（﹣1，y₁），（2，y₂）在抛物线y＝x²﹣2x+c上，则y₁ ， y₂的大小关系是.

查看试题解析
13. 如图，是二次函数 $y = a x^{2} + b x + c$ 的部分图象，由图象可知不等式 $a x^{2} + b x + c < 0$ 的解集是.

查看试题解析
14. 对于两个不相等的实数a，b，我们规定符号Max{a，b}表示a，b中的较大值，如：Max{2，4}=4，按照这个规定，方程Max{x，-x}=x²-2的解为.

查看试题解析
15. 如图，已知正方形ABCD的边长为6，E、F分别是AB、BC边上的点，且∠EDF＝45°，将△DAE绕点D逆时针旋转90°，得到△DCM若AE＝2，则FM的长为 .

查看试题解析

三、解答题

16. 用适当的方法解下列一元二次方程：

(1)、 $x (x - 3) + x = 3$

(2)、 $3 x^{2} - 1 = 4 x$

查看试题解析
17. 如图为二次函数y＝-x²-x＋2的图象，试根据图象回答下列问题：

(1)、方程-x²-x＋2＝0的解为；

(2)、当y＞0时，x的取值范围是；

(3)、当-3＜x＜0时，y的取值范围是.

查看试题解析
18. 已知关于x的方程 $(m + 1) x^{2} + 2 m x + m - 3 = 0$ ，

(1)、当 $m$ 取何值时，方程有两个不相等的实数根？

(2)、给 $m$ 选取一个合适的整数，使方程有两个有理根，并求出这两个根.

查看试题解析
19. 如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）.

（ 1 ）请画出将△ABC向左平移4个单位长度后得到的图形△A₁B₁C₁；

（ 2 ）请画出△ABC关于点（1，0）成中心对称的图形△A₂B₂C₂；

（ 3 ）若△A₁B₁C₁绕点M旋转可以得到△A₂B₂C₂ ，请直接写出点M的坐标；

（ 4 ）在x轴上找一点P，使PA+PB的值最小，请直接写出点P的坐标.

查看试题解析
20. 如图，利用一面墙（墙长25米），用总长度52米的栅栏（图中实线部分）围成一个矩形围栏ABCD，且中间共留两个1米的小门，设栅栏BC长为x米.

(1)、AB＝米（用含x的代数式表示）；

(2)、若矩形围栏ABCD面积为240平方米，求栅栏BC的长.

查看试题解析
21. 某企业研发了一种新产品，已知这种产品的成本为40元/件，且年销售量y（万件）与售价x（元/件）的函数关系式为y＝ ${\begin{array}{l} - 2 x + 200 (60 \leq x < 80) \\ - x + 110 (80 \leq x \leq 90) \end{array}$ .

(1)、当售价为85元/件时，年销售量为万件；

(2)、当售价为多少时，销售该产品的年利润最大？最大利润是多少？

查看试题解析
22. 如图所示，在平面直角坐标系中，抛物线 $y = \frac{1}{2} x^{2} + b x + c$ 经过点 $A (0 ， 2)$ 和 $B (1 ， \frac{3}{2})$ .

(1)、求抛物线的解析式；

(2)、已知点C与点A关于此抛物线的对称轴对称，求点C的坐标；

(3)、点D在抛物线上，且横坐标为4，记抛物线在点A，D之间的部分（含点A，D）为图像G，若图像G向下平移t（ $t > 0$ ）个单位后与直线BC只有一个公共点，求t的取值范围.

查看试题解析
23. 已知∠ACD=90°，AC=DC，MN是过点A的直线，过点D作DB⊥MN于B，连接CB.

(1)、问题发现：如图①，过点C作CE⊥CB，与MN交于点E，则容易发现BD与EA之间的数量关系为　， BD，AB，CB之间的数量关系为　　；

(2)、拓展探究：当MN绕点A旋转到如图②的位置时，试猜想线段BD，AB，CB之间的数量关系，并证明.

(3)、解决问题：当MN绕点A旋转到如图③的位置时（点C，D在直线MN的两侧），若此时∠BCD=30°，BD=2，则CB= 　 .

查看试题解析

$x$	1.1	1.2	1.3	1.4
$a x^{2} + b x + c$	-0.59	0.84	2.29	3.76