河南省南阳市淅川县2022-2023学年九年级上学期期中数学试题
试卷更新日期:2022-12-19 类型:期中考试
一、单选题
-
1. 下列各式是最简二次根式的是( )A、 B、 C、 D、2. 下列运算正确的是( )A、 B、4-=3 C、= D、2÷=23. 若m、n是一元二次方程x2+2x﹣2021=0的两个实数根,则2m+2n﹣mn的值为( )A、2021 B、2019 C、2017 D、20154. 已知 , 则的值为( )A、 B、 C、 D、5. 如图,一艘船向东航行,上午8时到达O处,测得一灯塔A在船的北偏东60°方向,且与船相距海里;上午11时到达B处,测得灯塔在船的正北方向.则这艘船航行的速度为( )
 A、海里/时 B、海里/时 C、海里/时 D、海里/时6. 若关于x的一元二次方程x2+3x﹣k=0有两个不相等的实数根,则实数k的取值范围为( )A、k>﹣ B、k≥﹣ C、k<﹣ D、k≤﹣7. 如图,已知AB∥CD∥EF,它们依次交直线l1、l2于点A、D、F和点B、C、E,如果AD:DF=3:1,BE=10,那么CE等于( )
A、海里/时 B、海里/时 C、海里/时 D、海里/时6. 若关于x的一元二次方程x2+3x﹣k=0有两个不相等的实数根,则实数k的取值范围为( )A、k>﹣ B、k≥﹣ C、k<﹣ D、k≤﹣7. 如图,已知AB∥CD∥EF,它们依次交直线l1、l2于点A、D、F和点B、C、E,如果AD:DF=3:1,BE=10,那么CE等于( )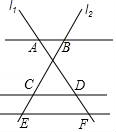 A、 B、 C、 D、8. 如图是某公园在一长35m,宽23m的矩形湖面上修建的等宽的人行观景曲桥,它的面积恰好为原矩形湖面面积的 ,求人行观景曲桥的宽.若设人行观景曲桥的宽为xm,则x满足的方程为()
A、 B、 C、 D、8. 如图是某公园在一长35m,宽23m的矩形湖面上修建的等宽的人行观景曲桥,它的面积恰好为原矩形湖面面积的 ,求人行观景曲桥的宽.若设人行观景曲桥的宽为xm,则x满足的方程为() A、 B、 C、 D、9. 在△ABC中,∠ACB=90°,用直尺和圆规在AB上确定点D,使△ACD∽△CBD,根据作图痕迹判断,正确的是( )A、
A、 B、 C、 D、9. 在△ABC中,∠ACB=90°,用直尺和圆规在AB上确定点D,使△ACD∽△CBD,根据作图痕迹判断,正确的是( )A、 B、
B、 C、
C、 D、
D、 10. 如图,在中,点E在BC上,且.D是AC的中点,AE、BD交于点F,则的值为( )
10. 如图,在中,点E在BC上,且.D是AC的中点,AE、BD交于点F,则的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 已知 ,则12. 如图所示,△ABC的顶点在正方形网格的格点上,则的值为.
 13. 如图是小孔成像原理示意图,若点O到AB的距离是18cm,O到CD的距离是6cm,物体AB的高度是9cm,则像CD的高度是cm.
13. 如图是小孔成像原理示意图,若点O到AB的距离是18cm,O到CD的距离是6cm,物体AB的高度是9cm,则像CD的高度是cm.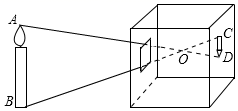 14. 如图,在与中, , , 连接BD、CE,若 , 则为.
14. 如图,在与中, , , 连接BD、CE,若 , 则为. 15. 如图,在Rt△ABC中,∠A=90°,AB=AC,BC= +1,点M,N分别是边BC,AB上的动点,沿MN所在的直线折叠∠B,使点B的对应点B′始终落在边AC上,若△MB′C为直角三角形,则BM的长为 .
15. 如图,在Rt△ABC中,∠A=90°,AB=AC,BC= +1,点M,N分别是边BC,AB上的动点,沿MN所在的直线折叠∠B,使点B的对应点B′始终落在边AC上,若△MB′C为直角三角形,则BM的长为 .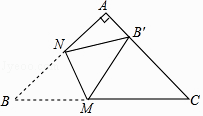
三、解答题
-
16.(1)、计算:;(2)、计算:;(3)、解方程:.(4)、解方程:;17. 先化简,再求值: , 其中.18. 已知:△ABC在坐标平面内,三个顶点的坐标为A(0,3)、B(3,4)、C(2,2).(正方形网格中,每个小正方形边长为1个单位长度)

( 1 )画出△ABC向下平移4个单位得到的△A1B1C1;
( 2 )以B为位似中心,在网格中画出△A2BC2 , 使△A2BC2与△ABC位似,且位似比2:1,直接写出C2点坐标是 ;
( 3 )△A2BC2的面积是 平方单位.
19. 如图,在△ABC中,AD平分∠BAC,E是AD上点,且BE=BD. (1)、求证:;(2)、若BD=1,CD=2,求的值.20. 已知关于x的方程(1)、求证:无论k取何值,该方程总有实数根;(2)、若等腰的一边长 , 另两边b、c恰好是该方程的两个根,求三角形另外两边的长.21. 越来越多太阳能路灯的使用,既点亮了城市的风景,也是我市积极落实节能环保的举措.某校学生开展综合实践活动,测量太阳能路灯电池板离地面的高度.如图,已知测倾器的高度为1.6米,在测点A处安置测倾器,测得点M的仰角 ,在与点A相距3.5米的测点D处安置测倾器,测得点M的仰角 (点A,D与N在一条直线上),求电池板离地面的高度 的长.(结果精确到1米;参考数据: )
(1)、求证:;(2)、若BD=1,CD=2,求的值.20. 已知关于x的方程(1)、求证:无论k取何值,该方程总有实数根;(2)、若等腰的一边长 , 另两边b、c恰好是该方程的两个根,求三角形另外两边的长.21. 越来越多太阳能路灯的使用,既点亮了城市的风景,也是我市积极落实节能环保的举措.某校学生开展综合实践活动,测量太阳能路灯电池板离地面的高度.如图,已知测倾器的高度为1.6米,在测点A处安置测倾器,测得点M的仰角 ,在与点A相距3.5米的测点D处安置测倾器,测得点M的仰角 (点A,D与N在一条直线上),求电池板离地面的高度 的长.(结果精确到1米;参考数据: ) 22. “早黑宝”葡萄品种是我省农科院研制的优质新品种在我省被广泛种植,邓州市某葡萄种植基地2017年种植“早黑宝”100亩,到2019年“早黑宝”的种植面积达到196亩。(1)、求该基地这两年“早黑宝”种植面积的平均增长率;(2)、市场查发现,当“早黑宝”的售价为20元千克时,每天售出200千克,售价每降价1元,每天可多售出50千克,为了推广直传,基地决定降价促销,同时减存已知该基地“早黑宝”的平均成本价为12元/千克,若使销售“早黑宝”天获利1750元,则售价应降低多少元?23. 【教材呈现】如图是华师九年级上删数学教材第77页的部分内容.
22. “早黑宝”葡萄品种是我省农科院研制的优质新品种在我省被广泛种植,邓州市某葡萄种植基地2017年种植“早黑宝”100亩,到2019年“早黑宝”的种植面积达到196亩。(1)、求该基地这两年“早黑宝”种植面积的平均增长率;(2)、市场查发现,当“早黑宝”的售价为20元千克时,每天售出200千克,售价每降价1元,每天可多售出50千克,为了推广直传,基地决定降价促销,同时减存已知该基地“早黑宝”的平均成本价为12元/千克,若使销售“早黑宝”天获利1750元,则售价应降低多少元?23. 【教材呈现】如图是华师九年级上删数学教材第77页的部分内容.如图,在中,点D、E分别是与的中点,根据画出的图形,可以猜想:
, 且
对此,我们可以用演绎推理给出证明.

【定理证明】
 (1)、请根据材料内容,结合图①,写出证明过程.(2)、【定理应用】
(1)、请根据材料内容,结合图①,写出证明过程.(2)、【定理应用】
如图②,四边形中,M、N、P分别为、、的中点,边、延长线交于点E, , 则的度数是.(3)、如图③,矩形中, , , 点E在边上,且.将线段绕点A旋转一周,得到线段 , M是线段的中点,直接写出旋转过程中线段长的最大值和最小值.