河南省南阳市淅川县2022-2023学年八年级上学期期中数学试题

试卷更新日期：2022-12-19 类型：期中考试

进入出卷网下载

一、单选题

1. $\sqrt{81}$ 的平方根是（）

A、±3 B、3 C、±9 D、9

查看试题解析
2. 估计20的算术平方根的大小在（　　）

A、2与3之间 B、3与4之间 C、4与5之间 D、5与6之间

查看试题解析
3. 下列运算正确的是（）

A、3a–2a=1 B、a²·a³=a⁶ C、(a–b)²=a²–2ab+b² D、(a+b)²=a²+b²

查看试题解析
4. 如图，已知∠ABC＝∠DCB，要使△ABC≌△DCB，只需添加一个条件，这个条件不能是（）

A、∠A＝∠D B、∠ACB＝∠DBC C、AC＝BD D、AB＝DC

查看试题解析
5. 下列命题是假命题的是 $($ $)$

A、同旁内角互补，两直线平行 B、若两个数的绝对值相等，则这两个数也相等 C、平行于同一条直线的两条直线也互相平行 D、全等三角形的周长相等

查看试题解析
6. 根据下列条件，不能画出唯一确定的△ABC的是（）

A、AB=3，BC=4，AC=6 B、AB=4，∠B=45°，∠A=60° C、AB=4，BC=3，∠A=30° D、∠C=90°，AB=8，AC=4

查看试题解析
7. 若 $(x - 5) (x + m) = x^{2} - 2 x + n$ ，则 $m$ ， $n$ 的值分别为（）

A、 $3$ ， $- 15$ B、 $3$ ， $15$ C、 $- 2$ ， $18$ D、 $- 2$ ， $- 18$

查看试题解析
8. 已知 $a + b = 2$ ， $a b = - 3$ ，则 $a^{2} - a b + b^{2}$ 的值是（）

A、11 B、12 C、13 D、14

查看试题解析
9. 已知 $10^{a} = 20$ ， $100^{b} = 50$ ，则 $\frac{1}{2} a + b + \frac{3}{2}$ 的值是（）

A、2 B、 $\frac{5}{2}$ C、3 D、 $\frac{9}{2}$

查看试题解析
10. 图（1）是一个长为2a，宽为 $2 b (a > b)$ 的长方形，用剪刀沿图中虚线（对称轴）剪开，把它分成四块形状和大小完全相同的小长方形，然后按图（2）那样拼成一个正方形，则中间空余的部分的面积是（）

A、ab B、 $(a + b)^{2}$ C、 $(a - b)^{2}$ D、 $a^{2} - b^{2}$

查看试题解析

二、填空题

11. 计算： $202 1^{2} - 2020 \times 2022 =$ .

查看试题解析
12. 若二次三项式 $x^{2} + 6 x + m^{2}$ 是关于x的完全平方式，则常数m＝.

查看试题解析
13. 我国传统工艺中，油纸伞如图①制作非常巧妙，其中蕴含着数学知识.图②是撑开的油纸伞的截面示意图，已知 $A E = A F$ ， $G E = G F$ ，则 $△ A E G ≌ △$ 其依据是.

查看试题解析
14. $y = \sqrt{2 x - 5} + \sqrt{5 - 2 x} - 3$ ，则 $2 x y$ 的值为。

查看试题解析
15. 如图，在2×2的正方形网格中，线段AB、CD的端点均在格点上，则∠1+∠2＝°．

查看试题解析

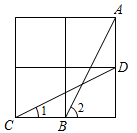
三、解答题

16. 计算

(1)、 $\sqrt{16} - \sqrt{(- 1)^{2}} - (\frac{1}{2})^{3} \div (\frac{1}{4})^{2}$

(2)、 $2022 \times 2020 - 202 0^{2}$ .

查看试题解析
17. 先化简，再求值.
${(x - y)}^{2} + (3 x - y) (x + y) - (x - 2 y) (x + 2 y)$ ，其中x，y满足 ${(x + 3)}^{2} + | y - 2 | = 0$ .

查看试题解析
18. 因式分解

(1)、 $a^{3} b - a b$ ；

(2)、 $(x + y)^{2} - (2 x + 2 y - 1)$ .

查看试题解析
19. 如图1，∠ABC＝90°，FA⊥AB于点A，D是线段AB上的点，AD＝BC，AF＝BD.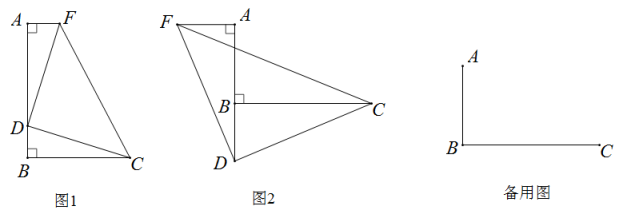

(1)、判断DF与DC的数量关系为，位置关系为.

(2)、如图2，若点D在线段AB的延长线上，过点A在AB的另一侧作AF⊥AB，并截取AF＝BD，连接DC，DF，CF，试说明（1）中结论是否成立，并说明理由.

查看试题解析
20. 阅读下列文字，并解决问题.
已知 $x^{2} y = 3$ ，求 $2 x y (x^{5} y^{2} - 3 x^{3} y - 4 x)$ 的值.
分析：考虑到满足 $x^{2} y = 3$ 的x，y的可能值较多，不可能逐一代入求解，故考虑整体思想，将 $x^{2} y = 3$ 整体代入.
解： $2 x y (x^{5} y^{2} - 3 x^{3} y - 4 x)$
$= 2 x^{6} y^{3} - 6 x^{4} y^{2} - 8 x^{2} y$
$= 2 (x^{2} y)^{3} - 6 (x^{2} y)^{2} - 8 x^{2} y$
$= 2 \times 3^{3} - 6 \times 3^{2} - 8 \times 3$
$= - 24$ .
请你用上述方法解决问题：

(1)、已知 $a b = 2$ ，求 $(2 a^{3} b^{2} - 3 a^{2} b + 4 a) \cdot (- 2 b)$ 的值；

(2)、已知 $x - \frac{1}{x} = 3$ ，求 $x^{2} + \frac{1}{x^{2}}$ 的值.

查看试题解析
21. 已知：AB＝AC，BD⊥AC，CE⊥AB，BD、CE相交于点F，

(1)、如图1，求证：BE＝CD.

(2)、如图2，连接AF，在不添加任何辅助线的情况下，请直接写出图2中所有的全等三角形.

查看试题解析

22. 【教材呈现】下图是华师版八年级上册数学教材第49页B组的第12题和第13题.

12.已知 $a + b = 3 ， a b = 2$ ，求 $a^{2} + b^{2}$ 的值.

13.已知 $a - b = 1 ， a^{2} + b^{2} = 25$ ，求 $a b$ 的值.

【例题讲解】老师讲解了第12题的两种方法：

方法一

方法二

∵ $a + b = 3$ ，

∴ $(a + b)^{2} = 9$ .

∴ $a^{2} + b^{2} + 2 a b = 9$ .

∵ $a b = 2$ ，

∴ $a^{2} + b^{2} = 9 - 2 a b = 9 - 4 = 5$ .

∵ $(a + b)^{2} = a^{2} + b^{2} + 2 a b$

∴ $a^{2} + b^{2} = (a + b)^{2} - 2 a b$ .

∵ $a b = 2 ， a + b = 3$ ，

∴ $a^{2} + b^{2} = 9 - 4 = 5$ .

(1)、【方法运用】请你任选第12题的解法之一，解答教材第49页B组的第13题.

(2)、【拓展】如图，在

△ A B C

中，

∠ A C B = 90 °

，分别以

A C

、

B C

为边向其外部作正方形

A C D E

和正方形

B C F G

.若

A C + B C = 6

，正方形

A C D E

和正方形

B C F G

的面积和为18，求

△ A B C

的面积.

查看试题解析

23. 如图，在△ABC中，∠ACB＝90°，AC＝6，BC＝8.点P从点A出发，沿折线AC—CB以每秒1个单位长度的速度向终点B运动，点Q从点B出发沿折线BC—CA以每秒3个单位长度的速度向终点A运动，P、Q两点同时出发.分别过P、Q两点作PE⊥l于E，QF⊥l于F.设点P的运动时间为t（秒）：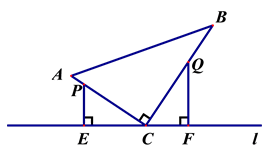

(1)、当P、Q两点相遇时，求t的值；

(2)、在整个运动过程中，求CP的长（用含t的代数式表示）；

(3)、当△PEC与△QFC全等时，直接写出所有满足条件的CQ的长.

查看试题解析