（人教版）2022-2023学年度第一学期九年级数学用列举法求概率期末复习

试卷更新日期：2022-12-17 类型：复习试卷

进入出卷网下载

一、单选题

1. 如图所示，电路连接完好，且各元件工作正常．随机闭合开关 $S_{1}$ ， $S_{2}$ ， $S_{3}$ 中的两个，能让两个小灯泡同时发光的概率是（）

A、0 B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{4}$

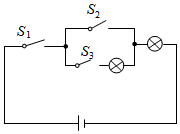查看试题解析
2. 为做好疫情防控工作，某学校门口设置了 $A$ ， $B$ 两条体温快速检测通道，该校同学王明和李强均从 $A$ 通道入校的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{3}{4}$

查看试题解析
3. 某医院计划选派护士支援某地的防疫工作，甲、乙、丙、丁4 名护士积极报名参加，其中甲是共青团员，其余3 人均是共产党员．医院决定用随机抽取的方式确定人选．若需从这4 名护士中随机抽取2 人，那么被抽到的两名护士都是共产党员的概率（）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{1}{2}$ D、1

查看试题解析
4. “二十四节气”是中华上古农耕文明的智慧结晶，被国际气象界普为“中国第五大发明”，小文购买了“二十四节气”主题邮票，他要将“立春”“立夏”“秋分”“大暑”四张邮票中的两张送给好朋友小乐．小文将它们背面朝上放在桌面上（邮票背面完全相同），让小乐从中随机抽取一张（不放回），再从中随机抽取一张，则小乐抽到的两张邮票恰好是“立春”和“立夏”的概率是（）

A、 $\frac{2}{3}$ B、 $\frac{1}{2}$ C、 $\frac{1}{6}$ D、 $\frac{1}{8}$

查看试题解析
5. 小明和他的爸爸妈妈共三人站成一排拍照，他的父母不相邻的概率是（）

A、 $\frac{1}{6}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
6. 有五张卡片的正面分别写有“喜”“迎”“二”“十”“大”，五张卡片洗匀后将其反面朝上放在桌面上，小明从中任意抽取两张卡片，恰好是“二十”的概率是（）

A、 $\frac{1}{10}$ B、 $\frac{1}{20}$ C、 $\frac{2}{5}$ D、 $\frac{1}{5}$

查看试题解析
7. 如图，在3×3的方格中，已有3个小正方形被涂黑，若在其余空白小正方形中任选一个涂黑，则所得图案是一个轴对称图形的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{2}{3}$ C、 $\frac{1}{3}$ D、 $\frac{1}{6}$

查看试题解析
8. 已知 $M (a ， b)$ 是平面直角坐标系 $x O y$ 中的点，其中 $a$ 是从1， 2，3三个数中任取的一个数， $b$ 是从1， 2 ， 3，4四个数中任取的一个数．定义“点 $M (a ， \overset{`}{b})$ 在直线 $x + y = n$ 上”为事件 $Q_{n} (2 \leq n \leq 7 ， n$ 为整数），则当 $Q_{n}$ 的概率最大时， $n$ 的所有可能的值为（）

A、5 B、4 或 5 C、5 或 6 D、4 或 6

查看试题解析
9. 有两辆车按1，2编号，方方和成成两人可以任意选坐一辆车，则两人同坐1号车的概率为（）

A、 $\frac{1}{6}$ B、 $\frac{1}{5}$ C、 $\frac{1}{4}$ D、 $\frac{1}{3}$

查看试题解析
10. 现有A，B两枚均匀的小立方体骰子，每个面上分别标有数字1，2，3，4，5，6。如果由小李同学掷A骰子朝上面的数字x，小明同学掷B骰子朝上面的数字y来确定点P的坐标（x，y），那么他们各掷一次所确定的点P落在已知直线y=-x+7的概率是（）

A、 $\frac{5}{36}$ B、 $\frac{1}{6}$ C、 $\frac{7}{36}$ D、 $\frac{1}{9}$

查看试题解析

二、填空题

11. 从甲、乙、丙、丁四名同学中随机选取两名同学去参加“喜迎二十大”的演讲比赛，则恰好抽到乙、丙同学的概率是．

查看试题解析
12. 在－2，－1，0，1，2这五个数中任取两数m，n，则二次函数 $y = {(x - m)}^{2} + n$ 的顶点在坐标轴上的概率为．

查看试题解析
13. 甲、乙、丙三个人相互传一个球，由甲开始发球，并作为第一次传球，则经过两次传球后，球回到甲手中的概率是。

查看试题解析
14. 小明与甲、乙两人一起玩“手心手背”的游戏．他们约定：如果三人中仅有一人出“手心”或“手背”，则这个人获胜；如果三人都出“手心”或“手背”，则不分胜负，那么在一个回合中，如果小明出“手心”，则他获胜的概率是．

查看试题解析
15. 如图，甲，乙两个转盘分别被三等分、四等分，各转动一次，停止转动后，将指针指向的数字分别记为 $a ， b$ ，使抛物线 $y = a x^{2} - 2 x + b$ 与 $x$ 轴有公共点的概率为．

查看试题解析

三、解答题

16. 如图，两个相同的可以自由转动的转盘A和B，转盘A被三等分，分别标有数字2，0， $- 1$ ；转盘B被四等分，分别标有数字3，2，-2，-3．如果同时任意转动转盘A、B，转盘停止时，两个指针指向转盘A、B上的对应数字分别为x，y（指针指在两个扇形的交线时，重新转动转盘）．小红和小兰用这两个转盘做游戏，若x与y的乘积是正数，则小红赢；若x与y的乘积是负数，则小兰赢．这个游戏对双方公平吗？请借助画树状图或列表的方法说明理由．

查看试题解析
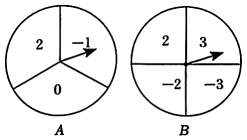
17. 一次圆桌会议设有4个座位，主持人坐在了如图所示的座位上，嘉宾甲、乙、丁3人等可能地坐到①、②、③中的3个座位上，请用所学的概率知识求嘉宾甲与乙相邻而坐的概率．

查看试题解析
18. 甲、乙两同学只有一张乒乓球比赛的门票，谁都想去，最后商定通过转盘游戏决定，游戏规则是：转动下面平均分成三个扇形且标有不同颜色的转盘，转盘连续转动两次，若指针前后所指颜色相同，则甲去；否则乙去．（如果指针恰好停在分割线上，那么重转一次，直到指针指向一种颜色为止）．你认为这个游戏公平吗？请说明理由．

查看试题解析

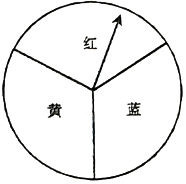
四、综合题

19. “中国梦”关系每个人的幸福生活，为展现石家庄人追梦的风采，我市某中学举行“中国梦·我的梦”的演讲比赛，赛后整理参赛学生的成绩，将学生的成绩分为A，B，C，D四个等级，并将结果绘制成如图所示的条形统计图和扇形统计图，但均不完整，请你根据统计图解答下列问题．

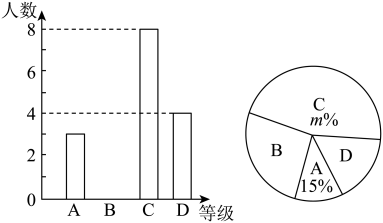(1)、参加比赛的学生人数共有名，在扇形统计图中，表示“D等级”的扇形的圆心角为度，图中m的值为；

(2)、补全条形统计图；

(3)、组委会决定从本次比赛中获得A和B等级的学生中，各选出1名去参加市中学生演讲比赛，已知A等级中女生有1名，B等级中男生有2人，请用“列表”或“画树状图”的方法求出所选2名学生中恰好是一名男生和一名女生的概率．

查看试题解析
20.

(1)、课本再现
教材中小颖为学校联欢会设计了一个“配紫色”的游戏，若转盘A转出了红色，转盘B转出了蓝色，就可以配成紫色．小贤和小明受到启发，也制作了两个“配紫色”的游戏转盘（如图1），规则如下：如图，A，B是两个可以自由转动的转盘，两人分别转动两个转盘，若其中一个转盘转出红色，另一个转盘转出蓝色，那么就能配成紫色．若配成紫色，则小贤赢，否则小明赢．这个游戏对双方公平吗？请说明理由．

(2)、在（1）中规则不变的情况下，请你在图2中设计一个游戏，使转动两个转盘能配成紫色的概率为 $\frac{1}{3}$ ．

查看试题解析

21. 小颖和小红两位同学在学习“概率”时，做掷骰子（质地均匀的正方体）实验.

(1)、他们在一次实验中共掷骰子

60

次，试验的结果如下：

朝上的点数	$1$	$2$	$3$	$4$	$5$	$6$
出现的次数	$7$	$9$	$6$	$8$	$20$	$10$

①填空：此次实验中“ $5$ 点朝上”的频率为；

②小红说：“根据实验，出现 $5$ 点朝上的概率最大.”她的说法正确吗？为什么？

(2)、小颖和小红在实验中如果各掷一枚骰子，那么两枚骰子朝上的点数之和为多少时的概率最大？试用列表或画树状图的方法加以说明，并求出其最大概率.

查看试题解析

22. 为落实“双减”政策，某校随机调查了50名学生平均每天完成书面作业所需时间的情况，根据调查数据绘制了如下不完整的统计图：

(1)、补全条形统计图：
分组
时间x（时）
A
$0 \leq x < 0.5$
B
$0.5 \leq x < 1$
C
$1 \leq x < 1.5$
D
$1.5 \leq x < 2$
E
$2 \leq x < 2.5$

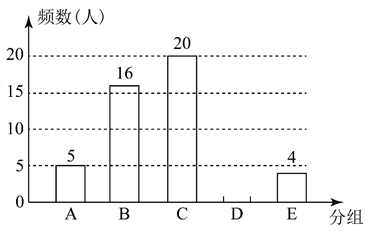(2)、若该校有学生2000人，估计每天完成书面作业的时间不足1.5小时的学生有人．

(3)、学校需要深入了解影响作业时间的因素，现从E组的4人中随机抽取2人进行谈话，已知E组中七、八年级各1人，九年级2人，则抽取的2人都是九年级学生的概率为多少？请用列表法或树状图说明．

查看试题解析
23. 为了有效落实“双减”政策，某校随机抽取部分学生，开展了“书面作业完成时间”问卷调查．根据调查结果，绘制了如下不完整的统计图表：
频数分布统计表
组别
时间 $x （$ 分钟 $）$
频数
$A$
$0 \leq x < 20$
6
$B$
$20 \leq x < 40$
14
$C$
$40 \leq x < 60$
$m$
$D$
$60 \leq x < 80$
$n$
$E$
$80 \leq x < 100$
4
根据统计图表提供的信息解答下列问题：

(1)、频数分布统计表中的 $m =$ ▲ ， $n =$ ▲ ；并补全频数分布直方图；

(2)、已知该校有1000名学生，估计书面作业完成时间在60分钟以上(含60分钟)的学生有多少人？

(3)、若 $E$ 组有两名男同学、两名女同学，从中随机抽取两名学生了解情况，请用列表或画树状图的方法，求出抽取的两名同学恰好是一男一女的概率．

查看试题解析

分组	时间x（时）
A	$0 \leq x < 0.5$
B	$0.5 \leq x < 1$
C	$1 \leq x < 1.5$
D	$1.5 \leq x < 2$
E	$2 \leq x < 2.5$

组别	时间 $x （$ 分钟 $）$	频数
$A$	$0 \leq x < 20$	6
$B$	$20 \leq x < 40$	14
$C$	$40 \leq x < 60$	$m$
$D$	$60 \leq x < 80$	$n$
$E$	$80 \leq x < 100$	4

（人教版）2022-2023学年度第一学期九年级数学 用列举法求概率 期末复习

一、单选题

二、填空题

三、解答题

四、综合题

（人教版）2022-2023学年度第一学期九年级数学用列举法求概率期末复习