(人教版)2022-2023学年度第一学期九年级数学 弧长及扇形的面积 期末复习
试卷更新日期:2022-12-17 类型:复习试卷
一、单选题
-
1. 如图,正方形的边长为4,以为直径的半圆O交对角线于点E,则阴影部分的面积( )
 A、 B、 C、 D、2. 已知半径为6的扇形的圆心角为60°,则该扇形的面积为( )A、4 B、6 C、4π D、6π3. 如图,扇形AOB圆心角为直角,OA=10,点C在上,以OA,CA为邻边构造▱ACDO,边CD交OB于点E,若OE=8,则图中两块阴影部分的面积和为( )
A、 B、 C、 D、2. 已知半径为6的扇形的圆心角为60°,则该扇形的面积为( )A、4 B、6 C、4π D、6π3. 如图,扇形AOB圆心角为直角,OA=10,点C在上,以OA,CA为邻边构造▱ACDO,边CD交OB于点E,若OE=8,则图中两块阴影部分的面积和为( ) A、10π-8 B、5π-8 C、25π-64 D、50π-644. 若扇形的半径为3,圆心角为160°,则它的面积为( )A、2π B、3π C、4π D、9π5. 如图,四边形ABCD为正方形,边长为4,以B为圆心、BC长为半径画 , E为四边形内部一点,且BE⊥CE,∠BCE=30°,连接AE,求阴影部分面积( )
A、10π-8 B、5π-8 C、25π-64 D、50π-644. 若扇形的半径为3,圆心角为160°,则它的面积为( )A、2π B、3π C、4π D、9π5. 如图,四边形ABCD为正方形,边长为4,以B为圆心、BC长为半径画 , E为四边形内部一点,且BE⊥CE,∠BCE=30°,连接AE,求阴影部分面积( ) A、 B、 C、 D、6. 如图,已知的半径为 , 弦直径 , , 则的长为( )
A、 B、 C、 D、6. 如图,已知的半径为 , 弦直径 , , 则的长为( ) A、 B、 C、 D、7. 如图,点A,B,C,D,E是⊙O上5个点,若AB=AO=2,将弧CD沿弦CD翻折,使其恰好经过点O,此时,图中阴影部分恰好形成一个“钻戒型”的轴对称图形,则“钻戒型”(阴影部分)的面积为( )
A、 B、 C、 D、7. 如图,点A,B,C,D,E是⊙O上5个点,若AB=AO=2,将弧CD沿弦CD翻折,使其恰好经过点O,此时,图中阴影部分恰好形成一个“钻戒型”的轴对称图形,则“钻戒型”(阴影部分)的面积为( ) A、 B、4π﹣3 C、4π﹣4 D、8. 如图,在扇形AOB中, , 点C在上,且的长为 , 点D在OA上,连接BD,CD,若点C,O关于直线BD对称,则图中阴影部分的面积为( )
A、 B、4π﹣3 C、4π﹣4 D、8. 如图,在扇形AOB中, , 点C在上,且的长为 , 点D在OA上,连接BD,CD,若点C,O关于直线BD对称,则图中阴影部分的面积为( ) A、 B、 C、 D、9. 把量角器和含角的三角板按如图方式摆放:零刻度线与长直角边重合,移动量角器使外圆弧与斜边相切时,发现中心恰好在刻度处,短直角边过量角器外沿刻度处(即 , ).则阴影部分的面积为( )
A、 B、 C、 D、9. 把量角器和含角的三角板按如图方式摆放:零刻度线与长直角边重合,移动量角器使外圆弧与斜边相切时,发现中心恰好在刻度处,短直角边过量角器外沿刻度处(即 , ).则阴影部分的面积为( )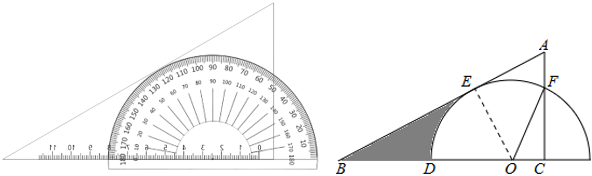 A、 B、 C、 D、10. 如图.将扇形翻折,使点A与圆心O重合,展开后折痕所在直线l与交于点C,连接 . 若 , 则图中阴影部分的面积是( )
A、 B、 C、 D、10. 如图.将扇形翻折,使点A与圆心O重合,展开后折痕所在直线l与交于点C,连接 . 若 , 则图中阴影部分的面积是( )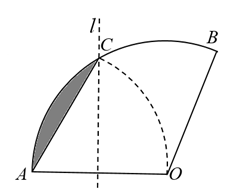 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 已知的半径为1, , 则的长度为 .12. 一个扇形的半径是 , 圆心角是 , 则此扇形的面积是 .13. 如图,扇形OAB中, , 以AO为直径作半圆.若 , 则阴影部分图形的周长为 .
 14. 一个扇形的面积为2πcm2 , 半径为4cm,则这个扇形的圆心角为.15. 如图,在矩形中,以点A为圆心,为半径画弧,交于点E;再以点B为圆心,以为半径画弧,交于点F,交前弧于点G,则图中两个阴影部分的面积之差的绝对值是.
14. 一个扇形的面积为2πcm2 , 半径为4cm,则这个扇形的圆心角为.15. 如图,在矩形中,以点A为圆心,为半径画弧,交于点E;再以点B为圆心,以为半径画弧,交于点F,交前弧于点G,则图中两个阴影部分的面积之差的绝对值是.
三、解答题
-
16. 弯制管道时,先按中心计算“展直长度”再下料,试计算图中所示管道的展直长度。(π≈3.14,单位:cm,精确到1cm,弯制管道的粗细不计)
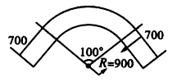 17. 如图,在四边形ABCD中,AD∥BC,AD=2,AB=2 , 以点A为圆心,AD为半径的圆与BC相切于点E,交AB于点F.若扇形AFD是一个圆锥的侧面,求这个圆锥的底面圆的半径.
17. 如图,在四边形ABCD中,AD∥BC,AD=2,AB=2 , 以点A为圆心,AD为半径的圆与BC相切于点E,交AB于点F.若扇形AFD是一个圆锥的侧面,求这个圆锥的底面圆的半径. 18. 如图,在△ABC中,∠ABC=90°,AB=BC=2,以点C为圆心,线段CA的长为半径作弧AD,交CB的延长线于点D,求出阴影部分的面积(结果保留π).
18. 如图,在△ABC中,∠ABC=90°,AB=BC=2,以点C为圆心,线段CA的长为半径作弧AD,交CB的延长线于点D,求出阴影部分的面积(结果保留π).
四、综合题
-
19. 如图,△ABC是⊙O的内接三角形,AD是⊙O的直径,∠ABC=60°.
 (1)、求:∠CAD的度数;(2)、若AD=6,求图中阴影部分的面积.20. 已知:在平面直角坐标系内,三个顶点的坐标分别为、、正方形网格中每个小正方形的边长均是1个单位长度 .
(1)、求:∠CAD的度数;(2)、若AD=6,求图中阴影部分的面积.20. 已知:在平面直角坐标系内,三个顶点的坐标分别为、、正方形网格中每个小正方形的边长均是1个单位长度 .
(1)画出绕点C顺时针旋转90°得到的 , 并求点B经过的路径长为▲ .
(2)以点为位似中心,在网格中画出 , 使与位似,且位似比为 , 点的坐标是▲
(3)求的面积.21. 如图,在矩形ABCD中,点E在边CB延长线上,AG⊥AE,交BC延长线于点G,边AG,DC交于点F,CF=BE,以AD为半径的⊙D交边BG于点P,Q,交AG于点M,延长DM交边QG于点N. (1)、求证:CG=AB.(2)、若AD=6,∠E=70°,求扇形ADM的面积.(3)、延长DC交⊙D于点H,且CH=NG,记AB=x,四边形AECF的面积为S,求S关于x的函数表达式.
(1)、求证:CG=AB.(2)、若AD=6,∠E=70°,求扇形ADM的面积.(3)、延长DC交⊙D于点H,且CH=NG,记AB=x,四边形AECF的面积为S,求S关于x的函数表达式.

