云南省昭通市巧家县2022-2023学年七年级上学期期中数学试题

试卷更新日期：2022-12-16 类型：期中考试

进入出卷网下载

一、单选题

1. $- 2022$ 的相反数是（）

A、 $- 2022$ B、 $- \frac{1}{2022}$ C、 $\frac{1}{2022}$ D、2022

查看试题解析
2. 将 $1000000$ 用科学记数法表示为（）

A、 $1 \times 1 0^{6}$ B、 $0.1 \times 1 0^{6}$ C、 $0.1 \times 1 0^{7}$ D、 $1 × 1 0^{7}$

查看试题解析
3. 下列各式中，是单项式的是（）

A、 $\frac{1}{n}$ B、 $\frac{x^{2} - y^{2}}{2}$ C、 $a b$ D、 $2 m n + m^{2} + 5$

查看试题解析
4. 计算 $- (2 a - 3 b)$ 的结果是（）

A、 $- 2 a + 3 b$ B、 $- 2 a - 3 b$ C、 $2 a + 3 b$ D、 $2 a - 3 b$

查看试题解析
5. 下列各组代数式中，是同类项的是（）

A、 $x^{3} y$ 和y B、3和0 C、x和 $4 x^{4}$ D、 $- m^{4} n$ 和 $2 m n^{4}$

查看试题解析
6. 下列有理数比较大小正确的是（）

A、 $- 5 = | - 5 |$ B、 $0 > | - 2 |$ C、 $- 2 < 2$ D、 ${(- 2)}^{2} < - 2$

查看试题解析
7. 下列计算正确的是（）

A、 $3 a - a = 3$ B、 $x^{2} + x^{3} = x^{5}$ C、 $5 x y - 2 x y = 3 x y$ D、 $4 a^{2} b - 2 a^{2} = 2 b$

查看试题解析
8. 若 $a = 1$ ， b的绝对值等于4，则 $a + b$ 的值为（）

A、 $- 3$ B、5 C、 $- 5$ 或 $- 3$ D、5或 $- 3$

查看试题解析
9. 在 $- 2022$ ， $- \frac{1}{7}$ ， $- (- 3)$ ， 0， ${(- 4)}^{2}$ ， $| - 2 |$ 中，既是负数又是整数的有（）

A、1个 B、2 C、3个 D、4个

查看试题解析
10. 已知a，b，c三个数在数轴上的位置如图所示，则下列结论正确的是（）

A、 $c < a$ B、 $a + c < 0$ C、 $a - c > 0$ D、 $a b c > 0$

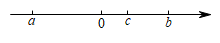查看试题解析
11. 下列说法错误的是（）

A、r $π$ 是分数 B、0是非负整数 C、一个数乘以-1，得这个数的相反数 D、一个数的倒数与本身同号

查看试题解析
12. 观察下列代数式： $- \frac{1}{2 a}$ ， $\frac{5}{4 a}$ ， $- \frac{9}{8 a}$ ， $\frac{13}{16 a}$ ， …．按此规律，则第n个代数式是（）

A、 ${(- 1)}^{n + 1} \frac{4 n - 3}{2 n a}$ B、 ${(- 1)}^{n + 1} \frac{4 n - 3}{2^{n} a}$ C、 ${(- 1)}^{n} \frac{4 n - 3}{2 n a}$ D、 ${(- 1)}^{n} \frac{4 n - 3}{2^{n} a}$

查看试题解析

二、填空题

13. 七年级（1）班第一次数学测试平均成绩是88分，小皓考了93分，记作“＋5分”，那么小张考了81分，记作．

查看试题解析
14. 多项式 $- 2 x^{2} - 5 x + 1$ 的二次项系数是．

查看试题解析
15. 有理数 $0.217$ 精确到百分位的近似数为．

查看试题解析
16. 若代数式 $x - 2 y$ 的值为5，则代数式 $2 x - 4 y + 1$ 的值为．

查看试题解析
17. 若 $| a + 3 | + {(b - 23)}^{2} = 0$ ，则 $a + b$ 的值为．

查看试题解析
18. 已知 $x ， y ， z$ 都是有理数， $x + y + z = 0$ ， $x y z \neq 0$ ，则 $\frac{| x |}{y + z} + \frac{| y |}{x + z} + \frac{| z |}{x + y}$ 的值是．

查看试题解析

三、解答题

19. 计算：

(1)、 $- 17 + | - 5 | + 3$ ．

(2)、 $- 2 \div \frac{1}{3} \times {(- 1)}^{4}$ ．

查看试题解析
20. 先化简，再求值： $4 a^{4} - 4 a b^{2} - (a^{4} - a b^{2} + 3 a^{4})$ ，其中 $a = - 3$ ， $b = 2$ ．

查看试题解析
21. 已知多项式 $x^{a + 1} y^{2} - x^{3} + x^{2} y - 1$ 是关于x、y的五次四项式，单项式 $- 8 x^{2} y^{3} z$ 的次数为b，c是最小的正整数，求 ${(a - b)}^{c + 1}$ 的值．

查看试题解析
22. 下表是黎老师开学第一周每天的步数记录情况表（超过： $10000$ 步的部分记为正；小于 $10000$ 步的部分记为负）：
星期
一
二
三
四
五
六
日
增减/步
＋145
$- 80$
＋80
＋135
＋80
$- 110$
$- 45$

(1)、求出黎老师开学第一周的总步数．

(2)、黎老师开学第一周步数中最多的一天比最少的一天多走了多少步？

查看试题解析
23. 中秋节期间某超市对顾客实行阶段优惠，规定如下：
一次性购物原价x元
优惠办法
$x ≤ 300$
无优惠
$300 < x \leq 500$
超过300的部分享九折优惠
$x > 500$
超过500的部分享七折优惠
例：小敏妈妈购买原价600元的物品，实际付款为： $300 + 0.9 \times (500 - 300) + 0.7 \times (600 - 500) = 550$ 元．

(1)、①当 $300 < x \leq 500$ 时，实际的付款金额为元（用含x的式子表示）．
②当 $x > 500$ 时，实际的付款金额为元（用含x的式子表示）．

(2)、羊羊妈妈去该超市两次购物，所购物品原价合计800元，其中第一次购物物品原价为a元 $(a > 500)$ ，用含a的式子表示羊羊妈妈两次购物的实际付款．

查看试题解析
24. 已知无论x、y取何值， ${(x + 2 y)}^{4} = a_{1} x^{4} + a_{2} x^{3} y + a_{3} x^{2} y^{2} + a_{4} x y^{3} + a_{5} y^{4}$ 恒成立，其中 $a_{1}$ ， $a_{2}$ ， $a_{3}$ ， $a_{4}$ ， $a_{5}$ 均为常数．代入不同x、y的值可逐步推导出 $a_{1}$ ， $a_{2}$ ， $a_{3}$ ， $a_{4}$ ， $a_{5}$ 的值，如代入 $x = 0$ ， $y = 1$ ，可得 $a_{5} = 16$ ．

(1)、代入 $x = 1$ ， $y = 0$ ，得 $a_{1} =$ ，代入 $x = 1$ ， $y = 1$ ，得 $a_{1} + a_{2} + a_{3} + a_{4} + a_{5} =$ ．

(2)、求 $\frac{{(a_{2} + a_{4} - 36)}^{2} - {(a_{3} - 25)}^{3}}{a_{1}}$ 的值．

查看试题解析

星期	一	二	三	四	五	六	日
增减/步	＋145	$- 80$	＋80	＋135	＋80	$- 110$	$- 45$

一次性购物原价x元	优惠办法
$x ≤ 300$	无优惠
$300 < x \leq 500$	超过300的部分享九折优惠
$x > 500$	超过500的部分享七折优惠