安徽省蚌埠市蚌山区2022-2023学年七年级上学期期中数学试题(11月)
试卷更新日期:2022-12-16 类型:期中考试
一、单选题
-
1. -2022的倒数是( )A、2022 B、 C、 D、2. 数3.14159精确到百分位约为( )A、3.14 B、3.15 C、3.141 D、3.1423. 据环球报报道:中国为防控疫情做出的巨大努力有目共睹,受到了世卫组织和国际权威公共卫生专家的称赞,其他一些国家也在寻求借鉴中国的经验和防控措施,截止9月17日报道前,境外累计确诊病例约78200000人次,将78200000用科学记数法表示应为( )A、 B、 C、 D、4. 等号左右两边一定相等的一组是( )A、 B、 C、 D、5. 如果 , 则a,b, ,的大小关系是( )A、 B、 C、 D、6. 在、、 , 这四个有理数中,负数有( )个.A、1个 B、2个 C、3个 D、4个7. 某企业今年一月份投入新产品的研发资金为a万元,以后每月投入新产品的研发资金与上月相比增长率都是20%.该厂今年三月份投入新产品的研发资金为b万元,则( )A、 B、 C、 D、8. 单项式与的和是 , 则( )A、-4 B、3 C、4 D、59. 当时,代数式的值为2023,则当时,代数式的值为( )A、 B、 C、2022 D、202310. 如图,三个图形都是边长为1的小正方形组成的网格,其中图1有1×1个小正方形,所有线段的和为4,图2有2×2个小正方形,所有线段的和为12,图3有3×3个小正方形,所有线段的和为24,按此规律,则第n个图中所有线段的和为()
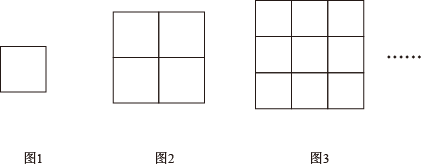 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 一运动员某次跳水的最高点离跳台2m,记作+2m,则水面离跳台10m可以记作 .12. 已知: , 且a<b,则=;13. 若 , , 则的值为14. 对于有理数a,b,n,d,若 , 则称a和b关于n的“相对关系值”为d,例如: , 则2和3关于1的“相对关系值”为3.(1)、求和5关于1的“相对关系值”为 .(2)、若m和n关于1的“相对关系值”为1,则的最大值为
三、解答题
-
15. 计算:(1)、(2)、16. 已知有理数a、b、c在数轴上对应的点如下图所示,

化简:
17. 先化简,再求值 , 其中x是最大的负整数,y的倒数是它本身.18. 如图,数轴上有六个点A,B,C,D,E,F,相邻两点之间的距离均为m(m为正整数),点B表示的数为 , 设这六个点表示的数的和为n, (1)、若m=2,则点F表示的数是 .(2)、已知点F表示的数是8.
(1)、若m=2,则点F表示的数是 .(2)、已知点F表示的数是8.①求m的值;
②求n的值.
19. 如图是一个长为a,宽为b的长方形,两个阴影图形都是一对底边长为1,且底边在长方形对边上的平行四边形. (1)、用含字母a,b的代数式表示长方形中空白部分的面积S;(2)、若 , , 求长方形中空白部分的面积.20. 已知多项式 , .(1)、若 , 化简;(2)、若的结果中不含有项以及项,求的值.21. 现有15箱苹果,以每箱25kg为标准,超过或不足的部分分别用正、负数来表示,记录如下表,请解答下列问题:
(1)、用含字母a,b的代数式表示长方形中空白部分的面积S;(2)、若 , , 求长方形中空白部分的面积.20. 已知多项式 , .(1)、若 , 化简;(2)、若的结果中不含有项以及项,求的值.21. 现有15箱苹果,以每箱25kg为标准,超过或不足的部分分别用正、负数来表示,记录如下表,请解答下列问题:标准质量的差 单位:
0
2
3
箱数
1
3
2
2
2
4
1
(1)、15箱苹果中,最重的一箱比最轻的一箱重多少千克?(2)、与标准质量相比,15箱苹果的总重量共计超过或不足多少千克?(3)、若苹果每千克售价为8元,则这15箱苹果全部售出共可获利多少元?22. 找规律:观察算式:;
;
;
;
……
(1)、按规律填空:① .
② .
(2)、由上面的规律计算: .23. 已知:a是单项式-xy2的系数,b是最小的正整数,c是多项式2m2n-m3n2-m-2的次数.请回答下列问题:(1)、请直接写出a、b、c的值.a= , b= , c= .(2)、数轴上,a、b、c三个数所对应的点分别为A、B、C,点A、B、C同时开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒1个单位长度和3个单位长度的速度向右运动,假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC.①t秒钟过后,AC的长度为 ▲ (用含t的关系式表示);
②请问:BC-AB的值是否会随着时间t的变化而改变?若变化,请说明理由;若不变,请求出其值.