2022-2023学年苏科版九年级上学期数学期末模拟试卷

试卷更新日期：2022-12-16 类型：期末考试

进入出卷网下载

一、单选题（每题2分，共12分）

1. 已知⊙O的半径是4，点P到圆心O的距离d为方程x²﹣4x﹣5＝0的一个根，则点P在（　　）

A、⊙O的内部 B、⊙O的外部 C、⊙O上或⊙O的内部 D、⊙O上或⊙O的外部

查看试题解析
2. 一个盒子中装有标号为1，2，3，4，5的五个小球，这些球除标号外都相同，从中随机摸出两个小球，则摸出的小球标号之和大于5的概率为（）

A、 $\frac{1}{5}$ B、 $\frac{2}{5}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
3. 如果数据 $x_{1}$ ， $x_{2}$ ， $⋯$ ， $x_{n}$ 的方差是3，则另一组数据 $2 x_{1}$ ， $2 x_{2}$ ， $⋯$ ， $2 x_{n}$ 的方差是（）

A、3 B、6 C、12 D、5

查看试题解析
4.
如图，在Rt△ABC中，∠ACB=90°，AC=2 $\sqrt{3}$ ，BC=6，动点P，Q分别在边AB，BC上，则CP+PQ的最小值为（）

A、3 $\sqrt{3}$ B、3+ $\frac{3 \sqrt{3}}{2}$ C、2 $\sqrt{3}$ D、2+ $\sqrt{3}$

查看试题解析
5. 如图， $R t △ A B C$ 中， $∠ C = 90 °$ ， O是AB边上一点， $⊙ O$ 与AC、BC都相切，若 $B C = 3$ ， $A C = 4$ ，则 $⊙ O$ 的半径为（）

A、1 B、2 C、 $\frac{5}{2}$ D、 $\frac{12}{7}$

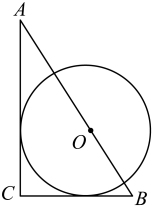查看试题解析
6. 在平面直角坐标系中，将抛物线y＝﹣x²+（m﹣1）x+m绕原点旋转180°，在旋转后的抛物线上，当x $>$ 4时，y随x的增大而增大，则m的范围是（）

A、m $>$ ﹣7 B、m $\geq$ ﹣7 C、m $<$ ﹣7 D、m $\leq$ ﹣7

查看试题解析

二、填空题（每题2分，共20分）

7. 已知 $\frac{x}{y} = \frac{3}{5}$ ，那 $\frac{x}{x + y}$ 的值为．

查看试题解析
8. 设α、β是方程x²+2x﹣2021＝0的两根，则α²+3α+β的值为．

查看试题解析
9. 如图，已知抛物线 $y = - \frac{4}{9} (x - 1) (x - 7)$ 与x轴交于A ， B两点，对称轴与抛物线交于点C ，与x轴交于点D ， ⊙C的半径为2，G为⊙C上一动点，P为AG的中点，则线段DP长的最大值为.

查看试题解析
10. 线段AB长10cm，点P在线段AB上，且满足 $\frac{B P}{A P}$ = $\frac{A P}{A B}$ ，那么AP的长为 cm．

查看试题解析
11. 如图，四边形ABCD是⊙O的内接四边形，⊙O的半径为2，∠D＝110°，则 $\overset{⌢}{A C}$ 的长为.

查看试题解析
12. 数学兴趣小组想测量一棵树的高度，在阳光下，一名同学测得一根长为1米的竹竿的影长为0.8米．同时另一名同学测量一棵树的高度时，发现树的影子不全落在地面上，有一部分影子落在教学楼的墙壁上（如图），其影长为1.2米，落在地面上的影长为2.4米，则树高为米．

查看试题解析
13. 如图，三个半圆依次相外切，它们的圆心都在x轴上，并与直线y= $\frac{\sqrt{3}}{3}$ x相切．设三个半圆的半径依次为r₁、r₂、r₃ ，则当r₁=1时，r₃= ．

查看试题解析
14. 如图，在⊙O中，AB是⊙O的内接正六边形的一边，BC是⊙O的内接正十边形的一边，则∠ABC＝°.

查看试题解析
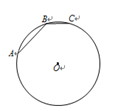15. 已知二次函数y＝ax²＋bx＋c的图象的顶点坐标为（1，m），与y轴的交点为（0，m－2），则a的值为.

查看试题解析
16. 如图，在⊙O中， $\overset{⌢}{A B}$ ＝ $\overset{⌢}{A C}$ ，AB＝10，BC＝12，D是 $\overset{⌢}{B C}$ 上一点，CD＝5，则AD的长为.

查看试题解析

三、解答题（共11题，共88分）

17. 解方程

(1)、16x²+8x＝3（公式法）

(2)、（3x+2）（x+3）＝x+14（配方法）

查看试题解析
18. 盒中有x个黑球和y个白球，这些球除颜色外无其他差别．若从盒中随机取一个球，它是黑球的概率是 $\frac{2}{5}$ ；若往盒中再放进1个黑球，这时取得黑球的概率变为 $\frac{1}{2}$ ．

(1)、填空：x= ， y=；

(2)、小王和小林利用x个黑球和y个白球进行摸球游戏．约定：从盒中随机摸取一个，接着从剩下的球中再随机摸取一个，若两球颜色相同则小王胜，若颜色不同则小林胜．求两个人获胜的概率各是多少?

查看试题解析

19. 甲、乙两班各10名同学参加“国防知识”比赛，其预赛成绩如下表：

	6分	7分	8分	9分	10分
甲班	1人	2人	4人	2人	1人
乙班	2人	3人	1人	1人	3人

(1)、填写下表：

	平均数	中位数	众数
甲班	8	8
乙班			7和10

(2)、利用方差判断哪个班的成绩更加稳定？

查看试题解析

20. 如图， $B D$ 是⊙O的直径， $A$ 是 $B D$ 延长线上的一点，点 $E$ 在⊙O上， $B C ⊥ A E$ ，交 $A E$ 的延长线于点 $C$ ， $B C$ 交⊙O于点 $F$ ，且 $E$ 为 $\overset{⌢}{D F}$ 的中点．

(1)、求证： $A C$ 是⊙O的切线；

(2)、若 $A D = 4$ ， $A E = 4 \sqrt{2}$ ，求 $B C$ 的长．

查看试题解析
21. 如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，F为AB延长线上一点，连接CF，DF.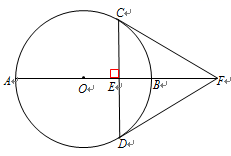

(1)、若OE＝3，BE＝2，求CD的长；

(2)、若CF与⊙O相切，求证DF与⊙O相切.

查看试题解析
22. 如图，二次函数的图象经过点（1，0），顶点坐标为（－1，－4）.

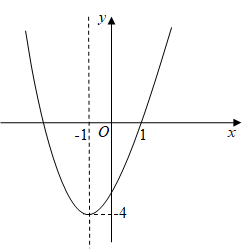(1)、求这个二次函数的表达式；

(2)、当－5＜x＜0时，y的取值范围为；

(3)、直接写出该二次函数的图象经过怎样的平移恰好过点（3，4），且与x轴只有一个公共点.

查看试题解析
23. 某超市销售一种饮料，每瓶进价为6元.当每瓶售价为10元时，日均销售量为160瓶.经市场调查表明，每瓶售价每增加0.5元，日均销售量减少10瓶.

(1)、当每瓶售价为11元时，日均销售量为瓶；

(2)、当每瓶售价为多少元时，所得日均总利润为700元？

(3)、当每瓶售价为多少元时，所得日均总利润最大？最大日均总利润为多少元？

查看试题解析
24. 如图，在⊙O中，弦AC与弦BD交于点P，AC＝BD.

(1)、求证AP＝BP；

(2)、连接AB，若AB＝8，BP＝5，DP＝3，求⊙O的半径.

查看试题解析
25. 已知函数y₁＝x＋1和y₂＝x²＋3x＋c（c为常数）.

(1)、若两个函数图象只有一个公共点，求c的值；

(2)、点A在函数y₁的图象上，点B在函数y₂的图象上，A，B两点的横坐标都为m.若A，B两点的距离为3，直接写出满足条件的m值的个数及其对应的c的取值范围.

查看试题解析
26. 如图，已知二次函数y=ax²+2x+c的图象经过点C（0，3），与x轴分别交于点A，点B（3，0）。点P是直线BC上方的抛物线上一动点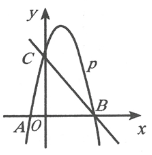

(1)、求二次函数y=ax²+2x+c的表达式；

(2)、连接PO，PC，并把△POC沿y轴翻折，得到四边形POPC.若四边形POP'C为菱形，请求出此时点P的坐标；

(3)、当点P运动到什么位置时，四边形ACPB的面积最大？求出此时P点的坐标和四边形ACPB的最大面积.

查看试题解析
27. 已知抛物线 $y = a x^{2} - 2 a x + c$ （a，c为常数， $a \neq 0$ ）经过点 $C (0 ， - 1)$ ，顶点为D．
（Ⅰ）当 $a = 1$ 时，求该抛物线的顶点坐标；

（Ⅱ）当 $a > 0$ 时，点 $E (0 ， 1 + a)$ ，若 $D E = 2 \sqrt{2} D C$ ，求该抛物线的解析式；

（Ⅲ）当 $a < - 1$ 时，点 $F (0 ， 1 - a)$ ，过点C作直线l平行于x轴， $M (m ， 0)$ 是x轴上的动点， $N (m + 3 ， - 1)$ 是直线l上的动点．当a为何值时， $F M + D N$ 的最小值为 $2 \sqrt{10}$ ，并求此时点M，N的坐标．

查看试题解析