江西省上饶市广丰区重点高中2022-2023学年高二上学期数学第三次月考试卷
试卷更新日期:2022-12-16 类型:月考试卷
一、单选题
-
1. 若点 在圆 的外部,则实数 的取值范围是( )A、 B、 C、 D、2. 现从6名学生干部中选出3名同学分别参加全校资源、生态和环保3个夏令营活动,则不同的选派方案的种数是( )A、20 B、90 C、120 D、2403. 如图,在正四棱柱中,是底面的中心,分别是的中点,则下列结论正确的是( )
 A、// B、 C、//平面 D、平面4. 在正方体 中, 为 的中点,则直线 与 所成的角为( )A、 B、 C、 D、5. 设是椭圆的上顶点,若上的任意一点都满足 , 则的离心率的取值范围是( )A、 B、 C、 D、6. 已知两点 , , 直线过点且与线段相交,则直线的斜率的取值范围是( )A、 B、或 C、 D、7. 若椭圆的左、右焦点分别为、 , 点P为椭圆C上一动点,则下列说法中不正确的是( )A、当点P不在x轴上时,的周长是6 B、当点P不在x轴上时,面积的最大值为 C、存在点P,使 D、的取值范围是8. 如图已知正方体 ,M , N分别是 , 的中点,则( )
A、// B、 C、//平面 D、平面4. 在正方体 中, 为 的中点,则直线 与 所成的角为( )A、 B、 C、 D、5. 设是椭圆的上顶点,若上的任意一点都满足 , 则的离心率的取值范围是( )A、 B、 C、 D、6. 已知两点 , , 直线过点且与线段相交,则直线的斜率的取值范围是( )A、 B、或 C、 D、7. 若椭圆的左、右焦点分别为、 , 点P为椭圆C上一动点,则下列说法中不正确的是( )A、当点P不在x轴上时,的周长是6 B、当点P不在x轴上时,面积的最大值为 C、存在点P,使 D、的取值范围是8. 如图已知正方体 ,M , N分别是 , 的中点,则( )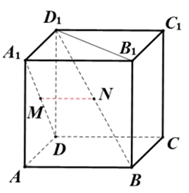 A、直线 与直线 垂直,直线 平面 B、直线 与直线 平行,直线 平面 C、直线 与直线 相交,直线 平面 D、直线 与直线 异面,直线 平面
A、直线 与直线 垂直,直线 平面 B、直线 与直线 平行,直线 平面 C、直线 与直线 相交,直线 平面 D、直线 与直线 异面,直线 平面二、多选题
-
9. 若直线与双曲线仅有一个交点,则a的值可以是( )A、4 B、2 C、1 D、10. 用0到9这10个数字.可组成( )个没有重复数字的四位偶数?A、 B、) C、 D、11. (多选)已知直线 , 则下列说法正确的是( ).A、直线的斜率可以等于0 B、若直线与轴的夹角为30°,则或 C、直线恒过点 D、若直线在两坐标轴上的截距相等,则或12. 某工程队有6辆不同的工程车,按下列方式分给工地进行作业,每个工地至少分1辆工程车,则下列结论正确的有( )A、分给甲、乙、丙三地每地各2辆,有120种分配方式 B、分给甲、乙两地每地各2辆,分给丙、丁两地每地各1辆,有180种分配方式 C、分给甲、乙、丙三地,其中一地分4辆,另两地各分1辆,有60种分配方式 D、分给甲、乙、丙、丁四地,其中两地各分2辆,另两地各分1辆,有1080种分配方式
三、填空题
-
13. 已知椭圆的焦距是8,椭圆上的某点到两个焦点的距离之和等于16,则椭圆的标准方程是 .14. 已知直线 和圆 相交于 两点.若 ,则 的值为 .15. 已知圆和圆交于两点,直线与直线平行,且与圆相切,与圆交于点 , 则 .16. 如图,在四棱锥中, , 底面为菱形,边长为2, , 平面 , 异面直线与所成的角为60°,若为线段的中点,则点到直线的距离为 .

四、解答题
-
17. 已知1,当k为何值时:(1)、方程表示双曲线;(2)、表示焦点在x轴上的双曲线;(3)、表示焦点在y轴上的双曲线.18. 如图,在以为顶点,母线长为的圆锥中,底面圆的直径长为2,是圆所在平面内一点,且是圆的切线,连接交圆于点 , 连接 , .
 (1)、求证:平面平面;(2)、若是的中点,连接 , , 当二面角的大小为时,求平面与平面所成锐二面角的余弦值.19. 已知抛物线 的准线与 轴的交点为 .(1)、求 的方程;(2)、若过点 的直线 与抛物线 交于 , 两点.求证: 为定值.20.(1)、解不等式 .(2)、若 , 求正整数n.(3)、若在如图1的电路中,只合上一个开关可以接通电路,有多少种不同的方法(用数字作答);在如图2的电路中,合上两个开关可以接通电路,有多少种不同的方法(用数字作答).
(1)、求证:平面平面;(2)、若是的中点,连接 , , 当二面角的大小为时,求平面与平面所成锐二面角的余弦值.19. 已知抛物线 的准线与 轴的交点为 .(1)、求 的方程;(2)、若过点 的直线 与抛物线 交于 , 两点.求证: 为定值.20.(1)、解不等式 .(2)、若 , 求正整数n.(3)、若在如图1的电路中,只合上一个开关可以接通电路,有多少种不同的方法(用数字作答);在如图2的电路中,合上两个开关可以接通电路,有多少种不同的方法(用数字作答).

