山西省长治市潞城区2022-2023学年九年级上学期12月月考数学试卷
试卷更新日期:2022-12-15 类型:月考试卷
一、单选题
-
1. “成语”是中华文化的瑰宝,是中华文化的微缩景观.成语“水中捞月”所描述的事件是( )A、必然事件 B、随机事件 C、不可能事件 D、无法确定2. 若式子在实数范围内有意义,则a的取值范围是( )A、 B、 C、 D、3. 一元二次方程根的情况是( )A、没有实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、无法确定4. 在如图所示的肉眼成像的示意图中,可能没有蕴含下列哪项初中数学知识( )
 A、平行线的性质 B、相似三角形的判定 C、位似图形 D、旋转5. 如图,在中, , , , 的对边分别为a,b,c,则下列结论中错误的是( )
A、平行线的性质 B、相似三角形的判定 C、位似图形 D、旋转5. 如图,在中, , , , 的对边分别为a,b,c,则下列结论中错误的是( ) A、 B、 C、 D、6. 中国古代在利用“计里画方”(比例缩放和直角坐标网格体系)的方法制作地图时,会利用测杆、水准仪和照板来测量距离.在如图所示的测量距离AB的示意图中,记照板“内芯”的高度为EF . 观测者的眼睛(图中用点C表示)与BF在同一水平线上,则下列结论正确的是( )
A、 B、 C、 D、6. 中国古代在利用“计里画方”(比例缩放和直角坐标网格体系)的方法制作地图时,会利用测杆、水准仪和照板来测量距离.在如图所示的测量距离AB的示意图中,记照板“内芯”的高度为EF . 观测者的眼睛(图中用点C表示)与BF在同一水平线上,则下列结论正确的是( )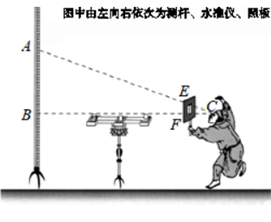 A、 B、 C、 D、7. 如图,在中, , D是的中点,若 , , 则等于( )
A、 B、 C、 D、7. 如图,在中, , D是的中点,若 , , 则等于( ) A、 B、 C、 D、8. 期末考试中出现了如图所示的一道题,小明同学从中任选了两个选项(每一个选项被选中的机会均等),请问小明答对题的概率是( )
A、 B、 C、 D、8. 期末考试中出现了如图所示的一道题,小明同学从中任选了两个选项(每一个选项被选中的机会均等),请问小明答对题的概率是( )(不定项选择题)下列选项中,正确的有( )
A.抛掷一枚硬币两次,出现一次正面、一次反面是必然事件
B.与是同类二次根式
C.直角三角形斜边上的中线等于斜边的一半
D.相似三角形的周长之比等于相似比
A、 B、 C、 D、9. 如图,在中, , 平分交于点D,点F在上,且 , 连接 , E为的中点,连接 , 则的长为( ) A、2 B、3 C、4 D、510. 如图,这是某拦河坝改造前后河床的横断面示意图, , 坝高 , 将原坡度的迎水坡面改为坡角为的斜坡 , 此时,河坝面宽减少的长度等于( )(结果精确到 , 参考数据)
A、2 B、3 C、4 D、510. 如图,这是某拦河坝改造前后河床的横断面示意图, , 坝高 , 将原坡度的迎水坡面改为坡角为的斜坡 , 此时,河坝面宽减少的长度等于( )(结果精确到 , 参考数据) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 从如图的四张印有品牌标志图案的卡片中任取一张,取出印有品牌标志的图案是轴对称图形的卡片的概率是 .
 12. 在一个不透明的布袋中,蓝色、黑色、白色的玻璃球共有60个,除颜色外其他完全相同.将布袋中的球摇匀,从中随机摸出一个球,记下它的颜色再放回去,通过多次摸球试验后发现,摸到黑色、白色的玻璃球的频率分别稳定在和 , 则口袋中蓝色玻璃球的个数很可能是 .13. 某小区原有一块长为50米,宽为40米的矩形健身场地,现计划在场内沿四周铺一圈宽度相等的小路,使场地剩余的面积为1824平方米,设这条小路的宽度为x米,则可列方程: .
12. 在一个不透明的布袋中,蓝色、黑色、白色的玻璃球共有60个,除颜色外其他完全相同.将布袋中的球摇匀,从中随机摸出一个球,记下它的颜色再放回去,通过多次摸球试验后发现,摸到黑色、白色的玻璃球的频率分别稳定在和 , 则口袋中蓝色玻璃球的个数很可能是 .13. 某小区原有一块长为50米,宽为40米的矩形健身场地,现计划在场内沿四周铺一圈宽度相等的小路,使场地剩余的面积为1824平方米,设这条小路的宽度为x米,则可列方程: . 14. 如图,某无人机兴趣小组在操场上开展活动,此时无人机在离地面米的D处,无人机测得操控者A的俯角为 , 测得教学楼顶点C处的俯角为 . 又经过人工测量测得操控者A和教学楼之间的水平距离为80米,则教学楼的高度为米(注:点A,B,C,D都在同一平面内,参考数据)
14. 如图,某无人机兴趣小组在操场上开展活动,此时无人机在离地面米的D处,无人机测得操控者A的俯角为 , 测得教学楼顶点C处的俯角为 . 又经过人工测量测得操控者A和教学楼之间的水平距离为80米,则教学楼的高度为米(注:点A,B,C,D都在同一平面内,参考数据) 15. 在一张矩形纸片中 , , M,N分别为 , 的中点,现将这张纸片按如图所示的方式折叠,使点B落在上的点F处,则的长为 .
15. 在一张矩形纸片中 , , M,N分别为 , 的中点,现将这张纸片按如图所示的方式折叠,使点B落在上的点F处,则的长为 .
三、解答题
-
16.(1)、计算: .(2)、解方程: .17. 已知:如图,在△ABC中,CD⊥AB,sinA = , CD =4,AB =5,求AD的长和tanB的值.
 18. 平安路上,多“盔”有你.在“交通安全宣传月”期间,某商店销售一批头盔,进价为每顶40元,售价为每顶68元,平均每周可售出100顶.商店计划将头盔降价销售,每顶售价不高于58元,经调查发现:每降价1元,平均每周可多售出20顶.该商店若希望每周获利4000元,则每顶头盔应降价多少元?19. 2022年3月3日晚,感动中国2021年度获奖人物揭晓.某校组织全体学生学习“感动中国”人物事迹并展示学习成果.校政教处随机抽取部分学生对其喜欢的学习成果展示形式进行了问卷调查(调查问卷如图所示),所有问卷全部收回,并将调查结果绘制成如下图所示的条形统计图和扇形统计图(均不完整).
18. 平安路上,多“盔”有你.在“交通安全宣传月”期间,某商店销售一批头盔,进价为每顶40元,售价为每顶68元,平均每周可售出100顶.商店计划将头盔降价销售,每顶售价不高于58元,经调查发现:每降价1元,平均每周可多售出20顶.该商店若希望每周获利4000元,则每顶头盔应降价多少元?19. 2022年3月3日晚,感动中国2021年度获奖人物揭晓.某校组织全体学生学习“感动中国”人物事迹并展示学习成果.校政教处随机抽取部分学生对其喜欢的学习成果展示形式进行了问卷调查(调查问卷如图所示),所有问卷全部收回,并将调查结果绘制成如下图所示的条形统计图和扇形统计图(均不完整).
学习成果展示形式调查问卷
同学你好!为传承民族精神,增强家国情怀,感悟榜样精神与力量,请同学们学习“感动中国”人物事迹并展示学习成果,请在表中选择一项你喜欢的形式(单选),在括号内打“√”,非常感谢你的合作.
A.书写心得感悟 ( )
B.绘制手抄报 ( )
C.讲述人物故事 ( )
D.举办话剧表满 ( )
E.其他 ( )

请根据统计图提供的信息,解答下列问题;
(1)、参与本次问卷调查的总人数为;补全条形统计图 .(2)、在扇形统计图中,求D部分圆心角的度数.(3)、小亮决定从四位获奖人物中选取两位学习并书写心得感悟,他将分别印有这四位人物的卡片(除人物内容外,其余完全相同)依次编号为Y,S,P,W,洗匀并放在不透明的盒子中,小亮从盒子中随机抽取一张卡片,放回后洗匀再取一张,请用列表或画树状图的方法求他抽到的两张卡片编号恰好是Y和P的概率.20. 阅读与思考【方法提炼】
解答几何问题常常需要添加辅助线,其中平移图形是重要的添加辅助线的策略.
【问题情境】
如图1,在边长为1的正方形网格中,点A,B,C,D都在格点上,求 . 小明在分析解题思路时想到了平移法:如图2,平移线段到 , 则 , 从而得 , 连接 , 再利用勾股定理逆定理证明是直角三角形,从而得出答案.

 (1)、【尝试应用】
(1)、【尝试应用】按照小明的思路,得出 .
(2)、如图3,在正方形网格中,A,B,C,D为格点,AB交CD于点O,求的值.21. 为加强疫情防控工作,某学校决定安装红外线体温检测仪,该设备通过探测人体红外辐射能量对进入测温区域的人员进行快速测温,无需人员停留和接触,安装说明书的部分内容如下表:名称
红外线体温检测仪
安装示意图

技术参数
最大探测角:
安装要求
本设备需要安装在垂直于水平地面的支架上,且
问题解决:学校要求测温区域的宽度为4m,师生身高设定为 . 当师生从A走到B时,即可测出人体温度.请你帮助学校确定该设备的安装高度 . (结果精确到m;参考数据 , )
22. 综合与实践(1)、【问题再现】课本中有这样一道概率题:如图1,这是一个可以自由转动的转盘,转动转盘,当转盘停止时,指针落在蓝色区域和橙色区域的概率分别是多少?请你解答.
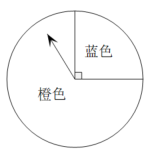 (2)、【类比设计】
(2)、【类比设计】在元旦晚会上班长想设计一个摇奖转盘.请你在图2中设计一个转盘,自由转动这个转盘,当它停止转动时,三等奖:指针落在红色区域的概率为 , 二等奖:指针落在白色区域的概率为 , 一等奖:指针落在黄色区域的概率为 .
 (3)、【拓展运用】
(3)、【拓展运用】在一次促销活动中,某商场为了吸引顾客,设立转盘,转盘被平均分为10份,顾客每消费200元转动1次,对准红1份,黄2份、绿3份区域,分别得奖金100元、50元、30元购物券,求转动1次所获购物券的平均数.
23. 综合与探究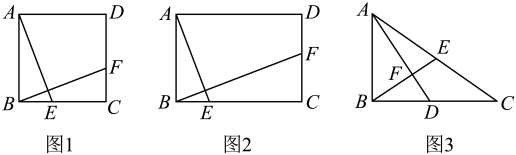 (1)、如图1,在正方形中,点分别在边上,且 , 请直接写出线段与的数量关系 .(2)、【类比探究】
(1)、如图1,在正方形中,点分别在边上,且 , 请直接写出线段与的数量关系 .(2)、【类比探究】如图2,在矩形中, , , 点分别在边上,且 , 请写出线段与的数量关系,并证明你的结论.
(3)、【拓展延伸】如图3,在中, , D为中点,连接 , 过点B作于点F,交于点E,若 , , 求的长.