山西省临汾市襄汾县2022-2023学年九年级上学期12月月考数学试卷

试卷更新日期：2022-12-15 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列各剪纸图案中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 从长度为 $1 c m ， 2 c m ， 3 c m ， 4 c m$ 的4根木棍中抽取了3根，能够构成三角形的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{5}$

查看试题解析
3. 已知⊙O的半径为3，点P到圆心O的距离为4，则点P与⊙O的位置关系是（　　）

A、点P在⊙O外 B、点P在⊙O上 C、点P在⊙O内 D、无法确定

查看试题解析
4. 某学习小组做“用频率估计概率”的实验时，统计了某一结果出现的频率，并绘制了如下表格．则该结果发生的概率约为（）
实验次数
100
500
1000
2000
4000
频率
0.37
0.32
0.345
0.339
0.333

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{5}$

查看试题解析
5. 如图， $B D$ 为 $⊙ O$ 的直径，过点A作 $⊙ O$ 的切线 $A C$ 交 $B D$ 的延长线于点C，连接 $A B$ ， $A D$ ，若 $∠ A B C = 30 °$ ，则 $∠ C =$ （）

A、 $20 °$ B、 $30 °$ C、 $35 °$ D、 $40 °$

查看试题解析
6. 已知某企业2月份的产值为250万元，经过技术革新，月产值不断增加，4月份产值达到360万元，若设该企业产值的月平均增长率为x，则可列方程为（）

A、 $250 (1 + x) = 360$ B、 $250 (1 + 2 x) = 360$ C、 $250 + 250 x^{2} = 360$ D、 $250 {(1 + x)}^{2} = 360$

查看试题解析
7. 如图， $⊙ O$ 为正方形 $A B C D$ 的外接圆，若 $B C = 2$ ，则 $⊙ O$ 的面积为（）

A、 $2 π$ B、 $3 π$ C、 $4 π$ D、 $8 π$

查看试题解析
8. 为做好疫情防控工作，在学校门口放置了 $A$ ， $B$ ， $C$ 三条体温检测通道，某日入校张老师与王同学走相同通道的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{5}$

查看试题解析
9. 如图， $A B$ 为 $⊙ O$ 的直径，C是 $⊙ O$ 上的一点，若 $∠ B C O = 35 °$ ， $A O = 2$ ，则 $\overset{⌢}{A C}$ 的长度为（）

A、 $\frac{2}{9} π$ B、 $\frac{5}{9} π$ C、 $π$ D、 $\frac{7}{9} π$

查看试题解析
10. 王刚在练习投篮，篮球脱手后的运动轨迹近似为如图所示的抛物线 $y = - 0.2 x^{2} + x + 2.25$ ，已知篮圈高 $3.05$ 米，王刚投篮时出手高度 $O B$ 为 $2.25$ 米，若要使篮球刚好投进篮圈C，则投篮时王刚离篮圈中心的水平距离为（）

A、 $2$ 米 B、 $3$ 米 C、 $4$ 米 D、 $5$ 米

查看试题解析

二、填空题

11. $x = 2$ 是关于x的一元二次方程 $x^{2} - 2 m x + 4 = 0$ 的解，则m= ．

查看试题解析
12. 初中生小明日常骑自行车上下学，某日小明沿地面一条直线骑行，自行车轮胎与这条直线的位置关系是．（填“相离”、“相交”或“相切”）

查看试题解析
13. 如图1，筒车是我国古代发明的一种水利灌溉工具，筒车盛水筒的运行轨迹是以O为圆心的一个圆，可简化为图2．若 $⊙ O$ 被水面所截的弦长 $A B = 8$ 米， $⊙ O$ 的半径为 $5$ 米，则筒车最低点距水面米．

查看试题解析
14. 在一个不透明的盒子里仅有白球若干个，为了知道这些白球的个数，小明同学往盒子里放了10个除颜色外其它都与原白球相同的红球，摇匀后随机抽取了8个球，其中有2个红球，则盒子中约有白球个．

查看试题解析
15. 如图，直线 $A B$ ， $B C$ ， $A C$ 与 $⊙ O$ 分别相切于点D，E，F，若 $∠ B = α$ ， $∠ C = β$ ， $∠ D E F = γ$ ，则 $γ =$ ．（用含 $α$ 、 $β$ 的式子表示）

查看试题解析

三、解答题

16. 在下列条件下求扇形的弧长．

(1)、半径为6，圆心角为 $90 °$ 的扇形．

(2)、面积为 $5 π$ ，半径为5的扇形．

查看试题解析
17. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ．

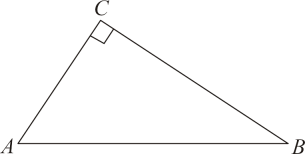(1)、实践与操作：利用尺规作 $△ A B C$ 的外接圆，圆心为点O（要求：尺规作图并保留作图痕迹，不写作法，标明字母）．

(2)、猜想与证明：若 $∠ C A B = 60 °$ ，试猜想线段 $A C$ 与 $⊙ O$ 半径r的数量关系，并加以证明．

查看试题解析
18. 某社区组织志愿者们为A，B，C，D四个小区的居民进行核酸检测，志愿者王芳、李明被分配到此次检测行动中来．用画树状图或列表法求王芳、李明被分配到同一个小区工作的概率．

查看试题解析
19. 如图， $A C$ 是 $⊙ O$ 的直径，P为半圆 $A C$ 的中点，连接 $A P$ 并延长至点B，使 $P B = A P$ ，连接 $C P 、 C B ， O P$ ．

(1)、求证： $B C$ 为 $⊙ O$ 的切线；

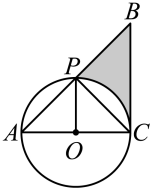(2)、若 $A C = 4$ ，求图中阴影部分的面积．

查看试题解析
20. 体育课上，王老师安排李明、王强、张三、田武四个同学练习传球，每个同学拿到球后随机传给下一个同学．

(1)、若李明第一个拿到球，他将球传给王强的概率为．

(2)、若从李明开始传球，则经过两次传球后，球回到李明手上的概率为多少？

查看试题解析

21. 阅读与思考

请阅读下列材料，并完成相应的任务．

在《阿基米德全集》中记述了伟大的古希腊数学家、哲学家、物理学家阿基米德提出的关于圆的一些问题，其中有这样一个问题：如图1， $A B$ 和 $B C$ 是 $⊙ O$ 的两条弦（即折线 $A B C$ 是圆的一条折弦）， $B C > A B$ ， $M$ 是 $\overset{⌢}{A B C}$ 的中点，则从点M向 $B C$ 所作垂线的垂足D是折弦 $A B C$ 的中点，即 $C D = D B + B A$ ．其部分证明过程如下：

证明：如图2，在 $C D$ 上截取 $C G = A B$ ，连接 $M A$ ， $M B$ ， $M C$ 和 $M G$ ．

∵ $M$ 是 $\overset{⌢}{A B C}$ 的中点，

∴ $M A = M C$ ，

∵ $∠ A = ∠ C$ ，

∴ $△ M A B ≌ △ M C G (S A S)$ ，

∴ $M B = M G$ ，

……

任务：

(1)、补全证明过程，

(2)、如图3，在

⊙ O

中，

\overset{⌢}{B D} = \overset{⌢}{C D}

，

D E ⊥ A C

，若

A B = 4

，

A C = 10

，

D E = 7

，则

O

到

D E

的距离是， O到

A C

的距离是，

⊙ O

的半径是．

查看试题解析

22. 综合与实践
问题情境：如图，将一个圆锥的侧面展开后可得到一个圆心角为 $n °$ ，半径为l的扇形 $B O B^{'}$ ，圆锥底面是一个半径为r的圆．母线 $O A$ 在展开图上对应的半径 $O A^{^{'}}$ 经过 $\overset{⌢}{B B^{'}}$ 的中点．

(1)、特例研究：当 $r = 3$ ， $l = 9$ 时，n= ，展开图上， $O A^{^{'}}$ 与OB的夹角为．

(2)、问题提出：求证： $n = \frac{360 r}{l}$ ．

(3)、问题解决：如图2，一种纸质圆锥形生日帽，底面直径为 $12 c m$ ，母线长也为 $12 c m$ ，为了美观，想在底面圆上一点A和与之相对的母线PB中点C之间拉一条细彩带进行装饰，求彩带长度的最小值．（提示：尝试画出圆锥侧面展开图）

查看试题解析
23. 综合与探究
已知二次函数 $y = a x^{2} - 2 a x + b$ ．

(1)、其图象的对称轴为直线．

(2)、若 $a > 0$ ，且该二次函数的图象经过点 $(- 2 ， c) ， (1 ， d) ， (2 ， e) ， (3 ， f)$ ，试比较c，d，e，f的大小，并说明理由．

(3)、若该二次函数的图象经过点 $(0 ， 2)$ ，且抛物线与x轴所围成的封闭图形内有4个整数点（不包括边界），求出a的取值范围．（注：横纵坐标均为整数的点为整数点）

查看试题解析

实验次数	100	500	1000	2000	4000
频率	0.37	0.32	0.345	0.339	0.333