河北省邯郸市丛台区联考2022--2023学年九年级上学期第二阶段质量评价数学试题

试卷更新日期：2022-12-15 类型：月考试卷

进入出卷网下载

一、单选题

1. 以下现象：①荡秋千；②呼啦圈；③跳绳；④转陀螺．其中是旋转的有（　　）

A、①② B、②③ C、③④ D、①④

查看试题解析
2. 方程2（x+1）²=1化为一般式为（）

A、2x²+4x+2=1 B、x²+4x=﹣1 C、2x²+4x+1=0 D、2x²+2x+1=0

查看试题解析
3. 关于频率和概率的关系，下列说法正确的是（）.

A、频率等于概率 B、当实验次数很大时，频率稳定在概率附近 C、当实验次数很大时，概率稳定在频率附近 D、实验得到的频率与概率不可能相等

查看试题解析
4. 如图，在⊙O中， $\overset{⌢}{A B}$ = $\overset{⌢}{A C}$ ，∠AOB=40°，则∠ADC的度数是（）

A、40° B、30° C、20° D、15°

查看试题解析
5. 如图所示，图中的每个阴影旋转一个角度后都能互相重合，这个角度可能是（　　）

A、30° B、45° C、120° D、90°

查看试题解析
6. 若（2，5）、（4，5）是抛物线 $y = a x^{2} + b x + c$ 上的两个点，则它的对称轴是（　　）

A、 $x = - \frac{b}{a}$ B、 $x = 1$ C、 $x = 2$ D、 $x = 3$

查看试题解析
7. 抛物线 $y = x^{2} - 2 x + 1$ 与坐标轴的交点个数为（）

A、无交点 B、1个 C、2个 D、3个

查看试题解析
8. 某市2019年平均房价为每平方米8000元，2021年平均房价降到每平方米7000元，设这两年平均房价年平均降低率为x，根据题意，下面所列方程正确的是（）

A、 $8000 {(1 + x)}^{2} = 7000$ B、 $8000 {(1 - x)}^{2} = 7000$ C、 $7000 {(1 - x)}^{2} = 7000$ D、 $7000 {(1 + x)}^{2} = 7000$

查看试题解析
9. 如图是二次函数y=﹣x²+2x+4的图象，使y≤1成立的x的取值范围是（）

A、－1 ≤ x ≤ 3 B、x ≤－1 C、x ≥ 1 D、x ≤－1或x ≥ 3

查看试题解析
10. 一个不透明的口袋中装有红球6个，黄球9个，绿球3个，这些球除颜色外没有其他任何区别．现从中任意摸出一个球．如果要使摸到绿球的概率为 $\frac{1}{4}$ ，需要在这个口袋中再放入绿球(　　)个

A、4 B、3 C、2 D、1

查看试题解析
11. 三角形的外心是三角形的（）

A、三条中线的交点 B、三条角平分线的交点 C、三边垂直平分线的交点 D、三条高所在直线的交点

查看试题解析
12. 如图，在平面直角坐标系中，以原点为圆心，半径为5的圆内有一点P（0，－3），那么经过点P的所有弦中，最短的弦的长为（）

A、4 B、5 C、8 D、10

查看试题解析
13.
物理某一实验的电路图如图所示，其中K₁ ， K₂ ， K₃ 为电路开关，L₁ ， L₂为能正常发光的灯泡．任意闭合开关K₁ ， K₂ ， K₃中的两个，那么能让两盏灯泡同时发光的概率为（　　）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{1}{2}$ D、 $\frac{1}{4}$

查看试题解析
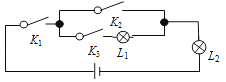14. 已知x为实数，且满足(x²＋3x)²＋2(x²＋3x)－3=0，那么x²＋3x的值为（）

A、1 B、－3或1 C、3 D、－1或3

查看试题解析
15. 已知 $y = - x^{2} + 4 x - 1$ ，当 $1 \leq x \leq 5$ 时，y的最小值是（）

A、2 B、3 C、 $- 8$ D、 $- 6$

查看试题解析
16. 将正方体骰子（相对面上的点数分别为 I 和 6 、 2 和 5 、 3 和 4 ）放置于水平桌面上，如图①．在图②中，将骰子向右翻滚 90 ．，然后在桌面上按逆时针方向旋转 90°．，则完成一次变换．若骰子的初始位置为图①所示的状态，那么按上述规则连续完成10次变换后，骰子朝上一面的点数是（）

A、6 B、5 C、3 D、2

查看试题解析

二、填空题

17. 如图，一只蚂蚁在正方形ABCD区域内爬行，点O是对角线的交点，∠MON=90°，OM，ON分别交线段AB，BC于M，N两点，则蚂蚁停留在阴影区域的概率为．

查看试题解析
18. 如图，将半径为2cm的圆形纸片折叠后，圆弧恰好经过圆心O，则折痕 $A B$ 的长为cm ．

查看试题解析
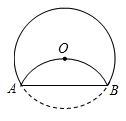19. 如图所示，已知抛物线 $C_{1}$ ，抛物线 $C_{2}$ 关于原点中心对称．如果抛物线 $C_{1}$ 的解析式为 $y = \frac{3}{4} (x + 2)^{2} - 1$ ，那么抛物线 $C_{2}$ 的顶点坐标是，解析式为．

查看试题解析

三、解答题

20. 如图， $△ A B C$ 三个顶点的坐标分别是 $A (1 ， 1) ， B (4 ， 2) ， C (3 ， 4)$ ，

（ 1 ）请画出 $△ A B C$ 向左平移6个单位后得到的 $△ A_{1} B_{1} C_{1}$ ，并写出 $B_{1}$ 的坐标；

（ 2 ）请画出 $△ A B C$ 关于原点对称的 $△ A_{2} B_{2} C_{2}$ ，并写出点 $B_{2}$ 的坐标；

（ 3 ）在x轴上求一点P使 $△ P A C$ 周长最小（保留作图痕迹，不写作法）

查看试题解析
21. 嘉淇同学用配方法推导一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 的求根公式时，对于 $b^{2} - 4 a c > 0$ 的情况，她是这样做的：
由于 $a \neq 0$ ，方程 $a x^{2} + b x + c = 0$ 变形为：
$x^{2} + \frac{b}{a} x = - \frac{c}{a}$ ， ……第一步
$x^{2} + \frac{b}{a} x + {(\frac{b}{2 a})}^{2} = - \frac{c}{a} + {(\frac{b}{2 a})}^{2}$ ， ……第二步
${(x + \frac{b}{2 a})}^{2} = \frac{b^{2} - 4 a c}{4 a^{2}}$ ， ……第三步
$x + \frac{b}{2 a} = \sqrt{\frac{b^{2} - 4 a c}{4 a^{2}}}$ ， ……第四步
$x = \frac{- b + \sqrt{b^{2} - 4 a c}}{2 a}$ ． ……第五步

(1)、嘉淇的解法从第步开始出现错误；事实上，当 $b^{2} - 4 a c > 0$ 时，方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 的求根公式是；

(2)、用配方法解方程： $x^{2} - 2 x - 24 = 0$ ．

查看试题解析
22. “中国梦”关系每个人的幸福生活，为展现石家庄人追梦的风采，我市某中学举行“中国梦·我的梦”的演讲比赛，赛后整理参赛学生的成绩，将学生的成绩分为A，B，C，D四个等级，并将结果绘制成如图所示的条形统计图和扇形统计图，但均不完整，请你根据统计图解答下列问题．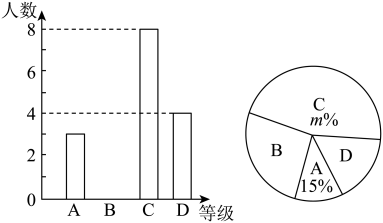

(1)、参加比赛的学生人数共有名，在扇形统计图中，表示“D等级”的扇形的圆心角为度，图中m的值为；

(2)、补全条形统计图；

(3)、组委会决定从本次比赛中获得A和B等级的学生中，各选出1名去参加市中学生演讲比赛，已知A等级中女生有1名，B等级中男生有2人，请用“列表”或“画树状图”的方法求出所选2名学生中恰好是一名男生和一名女生的概率．

查看试题解析
23. 如图，AB是半圆O的直径，C、D是半圆O上的两点，且OD∥BC，OD与AC交于点E．

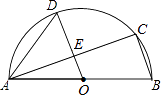(1)、若∠B=70°，求∠CAD的度数；

(2)、若AB=4，AC=3，求DE的长．

查看试题解析
24. 九（1）班数学兴趣小组经过市场调查，整理出某种商品在第x（1≤x≤90）天的售价与销售量的相关信息如下表：

时间x（天）

1≤x＜50

50≤x≤90

售价（元/件）

x＋40

90

每天销量（件）

200－2x

已知该商品的进价为每件30元，设销售该商品的每天利润为y元[

(1)、求出y与x的函数关系式；

(2)、问销售该商品第几天时，当天销售利润最大，最大利润是多少？

(3)、该商品在销售过程中，共有多少天每天销售利润不低于4800元？请直接写出结果.

查看试题解析
25. 如图，∠A=∠B=50°，P为AB中点，点M为射线AC上（不与点A重合）的任意点，连接MP，并使MP的延长线交射线BD于点N，设∠BPN=α．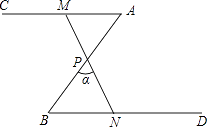

(1)、求证：△APM≌△BPN；

(2)、当MN=2BN时，求α的度数；

(3)、若△BPN的外心在该三角形的内部，直接写出α的取值范围．

查看试题解析
26. 如图①所示，将一个边长为2的正方形 $A B C D$ 和一个长为2、宽为1的长方形 $C E F D$ 拼在一起，构成一个大的长方形 $A B E F$ ．现将小长方形 $C E F D$ 绕点C顺时针旋转至长方形 $C E^{'} F^{'} D^{'}$ ，旋转角为 $α$ ．

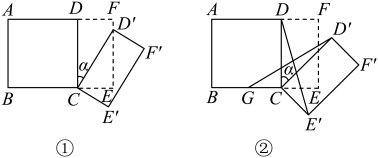(1)、当点 $D^{'}$ 恰好落在 $E F$ 边上时，求旋转角 $α$ 的值；

(2)、如图②，G为 $B C$ 中点，且 $0 ° < α < 90 °$ ，求证： $G D^{^{'}} = E^{^{'}} D$ ；

(3)、小长方形 $C E F D$ 绕点C顺时针旋转一周的过程中， $△ D C D^{'}$ 与 $△ C B D^{'}$ 能否全等？若能，直接写出旋转角 $α$ 的值；若不能，说明理由．

查看试题解析

时间x（天）	1≤x＜50	50≤x≤90
售价（元/件）	x＋40	90
每天销量（件）	200－2x