广东省佛山市南海区里水镇2022—2023学年九年级上学期第二次月考数学试题

试卷更新日期：2022-12-15 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列关于x的方程是一元二次方程的是（）

A、 $x^{2} + y = 1$ B、 $\frac{1}{x} = 1$ C、 $x^{2} - 4 x = 0$ D、 $a x^{2} + b x + c = 0$

查看试题解析
2. 如图，在菱形 $A B C D$ 中， $A C = 6 c m ， B D = 8 c m$ ，则菱形 $A B C D$ 的周长是（）

A、 $14 c m$ B、 $16 c m$ C、 $18 c m$ D、 $20 c m$

查看试题解析
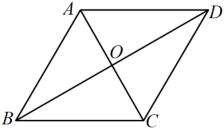3. 矩形、菱形、正方形都具有的性质是（）．

A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、对角线平分对角

查看试题解析
4. 如图，哪一个是太阳光下形成的影子？（）

A、 B、 C、 D、

查看试题解析
5. 如图所示，电路连接完好，且各元件工作正常．随机闭合开关 $S_{1}$ ， $S_{2}$ ， $S_{3}$ 中的两个，能让两个小灯泡同时发光的概率是（）

A、0 B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{4}$

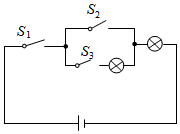查看试题解析
6. 已知关于x的一元二次方程 $x^{2} - 3 x - 2 = 0$ 的两实数根分别为 $x_{1} ， x_{2}$ ，则 $x_{1} x_{2} + x_{1} + x_{2}$ 的值为（）

A、 $- 1$ B、1 C、5 D、 $- 5$

查看试题解析
7. 在平面直角坐标系中，已知点 $A (- 4 ， 2)$ ， $B (- 6 ， - 4)$ ，以原点O为位似中心，相似比为2，把 $△ A B O$ 放大，则点B的对应点 $B^{^{'}}$ 的坐标（）

A、 $(- 3 ， - 2)$ B、 $(- 3 ， - 2)$ 或 $(3 ， 2)$ C、 $(- 12 ， - 8)$ D、 $(- 12 ， - 8)$ 或 $(12 ， 8)$

查看试题解析
8. 如图所示的几何体，其左视图是（）

A、 B、 C、 D、

查看试题解析
9. 在宽为30m，长为80m的矩形耕地上，修筑同样宽的三条道路（两条纵向，一条横向，横向与纵向互相垂直），把耕地分成六块作试验田，要使试验田总面积为1998平方米，问道路应为多宽？若设道路宽为xm，则根据题意可列方程来求解（）

A、 $30 \times 80 - 30 \times 2 x - 80 x = 1998$ B、 $30 \times 80 - 30 \times 2 x - 80 x - 2 x^{2} = 1998$ C、 $30 \times 80 - (30 - x) (80 - 2 x) = 1998$ D、 $(30 - x) (80 - 2 x) = 1998$

查看试题解析
10. 一般认为，如果一个人的肚脐以上的高度与肚脐以下的高度符合黄金分割，则这个人身材好．如图，是一个参加空姐选拔的选手的实际身高情况，如果要使身材好，那么她穿鞋子的高度最好为（） $c m$ ．（精确到 $1 c m$ ，参考数据：黄金分割比为 $\frac{\sqrt{5} - 1}{2} \approx 0.618$ ）

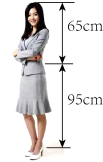A、5 B、8 C、10 D、12

查看试题解析

二、填空题

11. 若 $\frac{x}{y}$ = $\frac{2}{5}$ ，则 $\frac{x + y}{y}$ = ．

查看试题解析
12. 如图，在 $△ A B C$ 中，点D、E分别在边 $A B$ 、 $A C$ 上， $D E ∥ B C$ ．已知 $A E = 2$ ， $\frac{A D}{A B} = \frac{1}{3}$ ，则 $E C$ 的长是．

查看试题解析
13. 如图，在菱形 $A B C D$ 中，对角线 $A C$ 与 $B D$ 相交于点O，添加一个条件，使菱形 $A B C D$ 是正方形．

查看试题解析
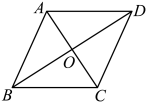14. 如图，将矩形ABCD折叠，使点C与点A重合，折痕为EF．若AF＝5，BF＝3，则AC的长为．

查看试题解析
15. 如图，在 $△ A B C$ 中， $A B = 8 c m$ ， $A C = 16 c m$ ，点P从点B开始沿 $B A$ 边向点A以每秒 $2 c m$ 的速度移动，点Q从点A开始沿 $A C$ 边向点C以每秒 $4 c m$ 的速度移动．如果P、Q分别从B、A同时出发，经过秒钟 $△ A P Q$ 与 $△ A B C$ 相似？

查看试题解析

三、解答题

16. 解方程： $x^{2} - 2 x - 5 = 0$

查看试题解析
17. 《九章算术》中记载了一种测量井深的方法．如图所示，在井口B处立一根垂直于井口的木杆BD，从木杆的顶端D点观察井内水岸C点，视线DC与井口的直径AB交于点E．如果测得AB＝1.8米，BD＝1米，BE＝0.2米．请求出井深AC的长．

查看试题解析
18. 已知：如图， $A D$ 是 $△ A B C$ 的角平分线，过点D分别作 $A C$ 和 $A B$ 的平行线交 $A B$ 于点E，交 $A C$ 于点F．

(1)、求证：四边形 $A E D F$ 是菱形；

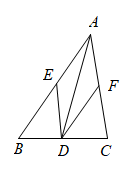(2)、若 $A E ＝ 5$ ， $A D ＝ 8$ ，则四边形 $A E D F$ 的面积为．

查看试题解析
19. 已知关于x的一元二次方程 $x^{2} - k x + k - 1 = 0$ ．

(1)、求证：无论k取何值，该方程总有实数根；

(2)、已知等腰三角形的一边a为2，另两边恰好是这个方程的两个根，求k的值．

查看试题解析

20. 一只不透明袋子中装有1个白球和若干个红球，这些球除颜色外都相同，某课外学习小组做摸球试验：将球搅匀后从中任意摸出1个球，记下颜色后放回、搅匀，不断重复这个过程，获得数据如下：

摸球的次数	200	300	400	1000	1600	2000
摸到白球的频数	72	93	130	334	532	667
摸到白球的频率	0.3600	0.3100	0.3250	0.3340	0.3325	0.3335

(1)、该学习小组发现，随着摸球次数的增多，摸到白球的频率在一个常数附近摆动，请直接写出这个常数（精确到0.01），由此估出红球有几个？

(2)、在这次摸球试验中，从袋中随机摸出1个球，记下颜色后放回，再从中随机摸出1个球，利用画树状图或列表的方法表示所有可能出现的结果，并求两次摸到的球恰好1是个白球，1个是红球的概率．

查看试题解析

21. 一只不透明袋子中装有1个白球和若干个红球，这些球除颜色外都相同，某课外学习小组做摸球试验：将球搅匀后从中任意摸出1个球，记下颜色后放回、搅匀，不断重复这个过程，获得数据如下：

摸球的次数	200	300	400	1000	1600	2000
摸到白球的频数	72	93	130	334	532	667
摸到白球的频率	0.3600	0.3100	0.3250	0.3340	0.3325	0.3335

(1)、该学习小组发现，随着摸球次数的增多，摸到白球的频率在一个常数附近摆动，请直接写出这个常数（精确到0.01），由此估出红球有几个？

查看试题解析

22. 某商店将进价为8元的商品按每件10元售出，每天可售出200件，现在采取提高商品售价减少销售量的办法增加利润，如果这种商品每件的销售价每提高0.5元，其销售量就减少10件，

(1)、应将每件售价提高多少元时，才能使每天利润为640元？

(2)、店主想要获得每天800元的利润，小红同学认为不可能．你同意小红同学的说法吗？请用所学知识说明理由．

查看试题解析
23.

(1)、如图1，四边形 $A B C D$ 是正方形，点E是 $A D$ 边上的一个动点，以 $C E$ 为边在 $C E$ 的右侧作正方形 $C E F G$ ，连接 $D G 、 B E$ ，判断线段 $D G$ 与 $B E$ 的数量关系并说明理由；

(2)、如图2，四边形 $A B C D$ 是矩形， $A B = 3 ， B C = 6$ ，点E是 $A D$ 边上的一个动点，以 $C E$ 为边在 $C E$ 的右侧作矩形 $C E F G$ ，且 $C G ： C E = 1 ： 2$ ，连接 $D G 、 B E$ ．判断线段 $D G$ 与 $B E$ 又有怎样的数量关系，并说明理由；

(3)、如图3，在（2）的条件下，连接 $B G$ ，求 $2 B G + B E$ 的最小值．

查看试题解析
24. 如图在平面直角坐标系中，直线 $l_{1} ： y = - x + 3$ 与x轴交于点A，与y轴交于点B，直线 $l_{2} ： y = 2 x$ 与直线 $l_{1}$ 交于点P．

(1)、A点坐标为， P点坐标为；

(2)、在线段 $A B$ 上有一个动点M，过M点作直线 $M N ∥ y$ 轴，与直线 $y = 2 x$ 相交于点N，若 $△ P M N$ 的面积为 $\frac{3}{4}$ ，求M点的坐标．

(3)、若点C为线段 $A B$ 上一动点，在平面内是否存在一点D，使得以点O，A，C，D为顶点的四边形是菱形，若存在请直接写出D点的坐标，若不存在请说明理由．

查看试题解析