安徽省芜湖市无为市2022—2023学年九年级上学期12月教学质量检测数学试题
试卷更新日期:2022-12-15 类型:月考试卷
一、单选题
-
1. 将抛物线向右平移2个单位长度,再向下平移5个单位长度,得到的抛物线的函数表达式为( )A、 B、 C、 D、2. 下列叙述正确的是( )A、平分弦的直径垂直于弦 B、三点确定一个圆 C、相等的圆心角所对的弧相等 D、经过圆心的每一条直线都是圆的对称轴3. 下列事件中,属于必然事件的是( )A、打开电视正在播广告 B、射击运动员只射击1次,恰好命中靶心 C、一组数据的方差越小,则这组数据的波动越小 D、任意购买一张电影票,座位号是3的倍数4. 将点绕原点逆时针旋转90°得到的点的坐标是( )A、 B、 C、 D、5. 如图,点A,B,C均在上,当时,的度数是( )
 A、25° B、30° C、40° D、50°6. 如图所示,已知矩形的边若以点A为圆心作 , 使三点中至少有一个点在圆内,且至少有一点在圆外,则的半径r的取值范围是( )
A、25° B、30° C、40° D、50°6. 如图所示,已知矩形的边若以点A为圆心作 , 使三点中至少有一个点在圆内,且至少有一点在圆外,则的半径r的取值范围是( ) A、 B、 C、 D、7. 若某银行经过两次降息,使三年期存款的年利率由4%降至3.24%,则平均每次降息的百分比是( )A、10% B、9% C、8% D、7%8. 如图,A是圆O上一点, 是直径, , ,点D在圆O上且平分弧 ,则 的长为( )
A、 B、 C、 D、7. 若某银行经过两次降息,使三年期存款的年利率由4%降至3.24%,则平均每次降息的百分比是( )A、10% B、9% C、8% D、7%8. 如图,A是圆O上一点, 是直径, , ,点D在圆O上且平分弧 ,则 的长为( ) A、 B、 C、 D、9. 李阿姨有三件上衣,分别为蓝色、白色和红色,有两条裙子,分别为灰色和黑色,某天她准备出门时,随机拿出一件上衣和一条裙子穿上,则恰好为白色上衣和灰色裙子的概率是( )A、 B、 C、 D、10. 如图,扇形圆心角为直角, , 点C在上,以 , 为邻边构造 , 边交于点E,若 , 则图中两块阴影部分的面积和为( )
A、 B、 C、 D、9. 李阿姨有三件上衣,分别为蓝色、白色和红色,有两条裙子,分别为灰色和黑色,某天她准备出门时,随机拿出一件上衣和一条裙子穿上,则恰好为白色上衣和灰色裙子的概率是( )A、 B、 C、 D、10. 如图,扇形圆心角为直角, , 点C在上,以 , 为邻边构造 , 边交于点E,若 , 则图中两块阴影部分的面积和为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
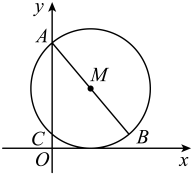
11. 五张卡片上分别写着 . 若从中随机抽出一张,则此卡片上的数为负数的概率是 .12. 如图,在平面直角坐标系中,以为圆心,为直径的圆与x轴相切,与y轴交于A,C两点,则的长为 .
 13. 对于二次函数y=ax2+3(a≠0),当x取x1 , x2(x1≠x2)时,函数值相等,则当x取x1+x2时,函数值为 .14. 如图,正方形内接于圆O,点E为上一点,连接 , 若 , , 则正方形的边长为 , 的长为 .
13. 对于二次函数y=ax2+3(a≠0),当x取x1 , x2(x1≠x2)时,函数值相等,则当x取x1+x2时,函数值为 .14. 如图,正方形内接于圆O,点E为上一点,连接 , 若 , , 则正方形的边长为 , 的长为 .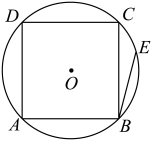
三、解答题
-
15. 如图,在平面直角坐标系中,、、.
 (1)、仅用无刻度的直尺,找出经过A,B,C三点的圆弧所在圆的圆心P,并直接写出圆心P的坐标为;(2)、点D坐标为 , 连接 , 则直线与圆P的位置关系为.16. 已知关于x的方程.(1)、判断该方程是否有实数根?(2)、设此方程的两实数根为 , , 且 , 求m的值.17. 如图,在中, , 将绕着点B逆时针旋转得到 , 点C,A的对应点分别为E,F,点E落在上,连接 .
(1)、仅用无刻度的直尺,找出经过A,B,C三点的圆弧所在圆的圆心P,并直接写出圆心P的坐标为;(2)、点D坐标为 , 连接 , 则直线与圆P的位置关系为.16. 已知关于x的方程.(1)、判断该方程是否有实数根?(2)、设此方程的两实数根为 , , 且 , 求m的值.17. 如图,在中, , 将绕着点B逆时针旋转得到 , 点C,A的对应点分别为E,F,点E落在上,连接 . (1)、若 . 则的度数为 ;(2)、若 , , 求的长.18. 如图,四边形内接于 , , 是的直径,连接 .
(1)、若 . 则的度数为 ;(2)、若 , , 求的长.18. 如图,四边形内接于 , , 是的直径,连接 .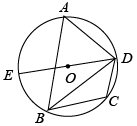 (1)、求的度数;(2)、若直径为4,求的长.19. 如图,某商场有一个可以自由转动的圆形转盘.规定:顾客购物元以上可以获得一次转动转盘的机会,当转盘停止时,指针落在哪一个区域就获得相应的奖品(指针指向两个扇形的交线时,当作指向右边的扇形).下表是活动进行中的一组统计数据:
(1)、求的度数;(2)、若直径为4,求的长.19. 如图,某商场有一个可以自由转动的圆形转盘.规定:顾客购物元以上可以获得一次转动转盘的机会,当转盘停止时,指针落在哪一个区域就获得相应的奖品(指针指向两个扇形的交线时,当作指向右边的扇形).下表是活动进行中的一组统计数据:转动转盘的次数n
落在“铅笔”的次数m
落在“铅笔”的频率
 (1)、转动该转盘一次,获得一瓶饮料的概率约为;(结果保留小数点后一位)(2)、经统计该商场每天约有名顾客参加扡奖活动,一瓶饮料和一支铅笔单价和为4元,估算支出的铅笔和饮料的奖品总费用是元,请计算该商场一瓶饮料和一支铅笔的单价.20. 某片果园有果树100棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低.若该果园每棵果树产果y(千克),增种果树x(棵),它们之间的函数关系为: .(1)、在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实8250千克?(2)、当增种果树多少棵时,果园的总产量w(千克)最大?最大产量是多少?21. 如图,点在圆O上,的平分线交圆O于点D,点C在的延长线上,且.
(1)、转动该转盘一次,获得一瓶饮料的概率约为;(结果保留小数点后一位)(2)、经统计该商场每天约有名顾客参加扡奖活动,一瓶饮料和一支铅笔单价和为4元,估算支出的铅笔和饮料的奖品总费用是元,请计算该商场一瓶饮料和一支铅笔的单价.20. 某片果园有果树100棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低.若该果园每棵果树产果y(千克),增种果树x(棵),它们之间的函数关系为: .(1)、在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实8250千克?(2)、当增种果树多少棵时,果园的总产量w(千克)最大?最大产量是多少?21. 如图,点在圆O上,的平分线交圆O于点D,点C在的延长线上,且. (1)、求证:是圆O的切线;(2)、若 , , 求圆O的半径.22. 2022年虎年新春,中国女足逆转韩国,时隔16年再夺亚洲杯总冠军;2022年国庆,中国女篮高歌猛进,时隔28年再夺世界杯亚军,一扫男足、男篮颓势,展现了中国体育的风采!为了培养青少年人才储备,雅礼某初中开展了“阳光体育活动”,决定开设足球、篮球、乒乓球、羽毛球、排球等球类活动,为了了解学生对这五项活动的喜爱情况,随机调查了一些学生(每名学生必选且只能选择这五项活动中的一种).根据以下统计图提供的信息,请解答下列问题:
(1)、求证:是圆O的切线;(2)、若 , , 求圆O的半径.22. 2022年虎年新春,中国女足逆转韩国,时隔16年再夺亚洲杯总冠军;2022年国庆,中国女篮高歌猛进,时隔28年再夺世界杯亚军,一扫男足、男篮颓势,展现了中国体育的风采!为了培养青少年人才储备,雅礼某初中开展了“阳光体育活动”,决定开设足球、篮球、乒乓球、羽毛球、排球等球类活动,为了了解学生对这五项活动的喜爱情况,随机调查了一些学生(每名学生必选且只能选择这五项活动中的一种).根据以下统计图提供的信息,请解答下列问题: (1)、本次被调查的学生有名;补全条形统计图;(2)、扇形统计图中“排球”对应的扇形的圆心角度数是;(3)、学校准备推荐甲、乙、丙、丁四名同学中的2名参加全市中学生篮球比赛,请用列表法或画树状图法分析甲和乙同学同时被选中的概率.23. 如图,D是等腰三角形底边的中点,过点 作 .
(1)、本次被调查的学生有名;补全条形统计图;(2)、扇形统计图中“排球”对应的扇形的圆心角度数是;(3)、学校准备推荐甲、乙、丙、丁四名同学中的2名参加全市中学生篮球比赛,请用列表法或画树状图法分析甲和乙同学同时被选中的概率.23. 如图,D是等腰三角形底边的中点,过点 作 .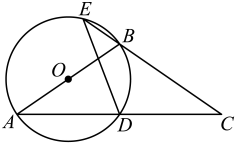 (1)、求证:是的直径;(2)、延长交于点E,连接 , 求证:;(3)、若 , , 求长.
(1)、求证:是的直径;(2)、延长交于点E,连接 , 求证:;(3)、若 , , 求长.