安徽省芜湖市无为市2022—2023学年八年级上学期12月教学质量检测数学试题

试卷更新日期：2022-12-15 类型：月考试卷

进入出卷网下载

一、单选题

1. 从平面镜里看到背后墙上电子钟的示数如图所示，这时的正确时间是（）

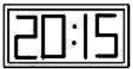A、21：05 B、21：15 C、20：15 D、20：12

查看试题解析
2. 下列运算与 ${(a^{4})}^{3}$ 的结果相等的是（　　）

A、 $a^{4} \cdot a^{3}$ B、 ${(a^{2})}^{5}$ C、 ${(a^{3} \cdot a^{3})}^{2}$ D、 $a^{24} \div a^{2}$

查看试题解析
3. 在下列计算中，不能用平方差公式计算的是（）

A、 $(m - n) (- m + n)$ B、 $(x^{3} - y^{3}) (x^{3} + y^{3})$ C、 $(- a - b) (a - b)$ D、 $(c^{2} - d^{2}) (d^{2} + c^{2})$

查看试题解析
4. 下列计算正确的是（　　）

A、 $3 x^{3} \cdot (- 2 x^{2}) = x^{5}$ B、 $3 a^{3} \cdot 8 a^{3} = 24 a^{9}$ C、 $- 3 a \cdot 2 a b = - 6 a^{2} b$ D、 $3 y^{2} \cdot 4 y^{2} = 12 y^{2}$

查看试题解析
5. 如图，直线 $a / / b$ ，等边 $△ A B C$ 的顶点C在直线b上，若 $∠ 1 = 40 °$ ，则 $∠ 2$ 的度数为（）

A、100° B、110° C、120° D、130°

查看试题解析
6. 计算： $\frac{5}{2} a \times 100 1^{2} - \frac{5}{2} a \times 99 9^{2} =$ （）

A、5000a B、1999a C、10001a D、10000a

查看试题解析
7. 如图， $△ A B C ≌ △ A D E$ ，点D在BC上，下列结论中不一定成立的是（）

A、 $∠ E = ∠ C$ B、 $B C = D E$ C、 $∠ B A D = ∠ C A E$ D、 $A B = B D$

查看试题解析
8. 在多项式 $16 x^{2} + 1$ 添加一个单项式，使得到的多项式能运用完全平方公式分解因式，则下列表述正确的是（　　）
嘉琪：添加 $\pm 8 x$ ， $16 x^{2} + 1 \pm 8 x = {(4 x \pm 1)}^{2}$ ；
陌陌：添加 $64 x^{4}$ ， $64 x^{4} + 16 x^{2} + 1 = {(8 x^{2} + 1)}^{2}$ ；
嘟嘟：添加 $- 1$ ， $16 x^{2} + 1 - 1 = 16 x^{2} = {(4 x)}^{2}$ ．

A、嘉琪和陌陌的做法正确 B、嘉琪和嘟嘟的做法正确 C、陌陌和嘟嘟的做法正确 D、三位同学的做法都正确

查看试题解析
9. 如图，在△ABC中，AB=AC=10，BC=12，AD=8，AD是BC边上的高．若P，Q分别是AD和AC上的动点，则PC+PQ的最小值是（）．

A、6 B、8 C、9.6 D、12

查看试题解析
10. 如图，有两个正方形纸板A，B，纸板A与B的面积之和为34．现将纸板B按甲方式放在纸板A的内部，阴影部分的面积为4．若将纸板A，B按乙方式并列放置后，构造新的正方形，则阴影部分的面积为（　　）

A、30 B、32 C、34 D、36

查看试题解析

二、填空题

11. 计算 ${(- 2 y^{3})}^{3}$ 的结果等于．

查看试题解析
12. 已知 $m + n = 4$ ， $m n = - 5$ ，则 $m^{2} n + m n^{2} =$ ．

查看试题解析
13. 如图， $△ A B C ≅ △ A D E$ ，且∠EAB=120°，∠B=30°，∠CAD=10°，∠CFD=°．

查看试题解析
14. 如图，在△ABC中，BC的垂直平分线MN交AB于点D．

(1)、若 $A D = 2$ ， $B D = 3$ ，则AC的长度x的取值范围为．

(2)、若 $∠ A = 6 0^{∘}$ ， ∠B为 $α$ ，则∠ACD为°．（用含 $α$ 的式子表示）

查看试题解析

三、解答题

15. 因式分解：

(1)、 $4 x^{2} y - 4 x y^{2} + y^{3}$ .

(2)、 $a^{2} (x - y) + b^{2} (y - x)$ .

查看试题解析
16. 已知将（x³+mx+n）（x²-3x+4）展开的结果不含x³和x²项，求m、n的值．

查看试题解析
17. 我们都知道“先看见闪电，后听见雷声”，那是因为在空气中光的传播速度比声音快．科学家们发现，光在空气中的传播速度约为 $3 \times 1 0^{8} m / s$ ，而声音在空气中的传播速度约为300m/s．问：在空气中光的传播速度是声音的多少倍？（结果用科学记数法表示）

查看试题解析
18. 如图，在 $△ A B C$ 中， $A B = A D = D C$ ．

(1)、若 $∠ B A D = 20 °$ ，求 $∠ C$ 的度数．

(2)、若 $∠ B A C = 78 °$ ，则 $∠ C$ 的度数为（直接写结果）．

查看试题解析
19. 已知 ${(2^{m})}^{n} = 4$ ， ${(a^{m})}^{2} \div a^{n} = a^{3}$ ．

(1)、求 $m n$ 和 $2 m - n$ 的值；

(2)、已知 $4 m^{2} - n^{2} = 15$ ，求 $m + n$ 的值．

查看试题解析
20. 如图，点D在等边 $△ A B C$ 的外部，E为 $B C$ 边上的一点， $A D = C D$ ， $D E$ 交 $A C$ 于点F， $A B ∥ D E$ ．

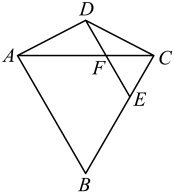(1)、判断 $△ C E F$ 的形状，并说明理由；

(2)、若 $B C = 10$ ， $C F = 4$ ，求 $D E$ 的长．

查看试题解析
21. 某种植基地有一块长方形和一块正方形实验田，长方形实验田每排种植（3a-b）株豌豆幼苗，种植了（3a＋b）排，正方形实验田每排种植（a＋b）株豌豆幼苗，种植了（a＋b）排，其中a＞b＞0．

(1)、正方形实验田比长方形实验田少种植豌豆幼苗多少株？

(2)、当a＝5，b＝2时，该种植基地这两块实验田一共种植了多少株豌豆幼苗？

查看试题解析
22. 如图，线段AB上两点C、D， $A C = B D$ ， $∠ A = ∠ B$ ， $A E = B F$ ，连接DE并延长至点M，连接CF并延长至点N，DM，CN交于点P， $M N ∥ A B$ ；

(1)、求证： $△ A D E ≅ △ B C F$ ；

(2)、求证： $△ P M N$ 是等腰三角形．

查看试题解析
23. 我们把多项式 a² + 2ab + b²及 a² - 2ab + b²这样的式子叫做完全平方式．如果一个多项式不是完全平方式，我们常做如下变形：先添加一个适当的项，使式子中出现完全平方式，再减去这个项，使整个式子的值不变，这种方法叫做配方法．配方法是一种亚要的解决问题的数学方法，不仅可以将一个看似不能分解的多项式分解因式，还能解决一些与非负数有关的问题或求代数式的最大值、最小值等．
例如：分解因式 x² + 2x - 3 ．
原式= （x² + 2x + 1 -1）- 3 = （x + 1）² - 4 =（x + 1 + 2）（x + 1 - 2）=（x + 3）（x -1 ）．
求代数式 2x² + 4x- 6 的最小值．
2x² + 4x - 6 = 2（x ² + 2x + 1 -1） - 6 = 2（x + 1）² - 8 ，可知当 x = -1 时， 2x² + 4x - 6 有最小值-8 ．
根据阅读材料用配方法解决下列问题：

(1)、填空：x²++36=(x+6)²； $3 m^{2} + 6 m = 3 (m + 1)^{2} -$ ；

(2)、利用配方法分解因式： $x^{2} - 6 x - 27$ ；（注意：用十字相乘法直接写出答案不给分）

(3)、当 x =时，多项式 $- x^{2} - 4 x + 1$ 的最大值为．

查看试题解析