安徽省蚌埠市2022-2023学年九年级上学期数学阶段性诊断数学试题

试卷更新日期：2022-12-15 类型：月考试卷

进入出卷网下载

一、单选题

1. $\tan 30 °$ 的值等于（）

A、 $\frac{\sqrt{3}}{3}$ B、 $\frac{\sqrt{3}}{2}$ C、1 D、 $\sqrt{3}$

查看试题解析
2. 已知在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $s i n A = \frac{\sqrt{3}}{2}$ ，则 $∠ B$ 的度数是（　　）

A、 $30 °$ B、 $45 °$ C、 $60 °$ D、 $75 °$

查看试题解析
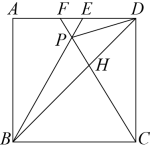
3. 如图，比例规是伽利略发明的一种画图工具，使用它可以把线段按一定比例伸长或缩短，它是由长度相等的两脚 $A D$ 和 $B C$ 交叉构成的．如果把比例规的两脚合上，用螺丝钉固定点O的位置，使 $O A = 3 O D ， O B = 3 O C$ ，然后张开两脚，使点A，B两个尖端分别在线段l的两个端点上，若 $C D = 5 c m$ ，则 $A B$ 的长是（　　）

A、5cm B、10 cm C、15 cm D、20 cm

查看试题解析
4. 如果线段 $a = 4 c m ， b = 16 c m$ ，那么a和b的比例中项是（　　）

A、 $4 c m$ B、 $8 c m$ C、 $\pm 8 c m$ D、 $16 c m$

查看试题解析
5. 如图，四边形 $A B C D$ 和四边形 $A^{'} B^{'} C^{'} D^{'}$ 是以点O为位似中心的位似图形，若四边形 $A B C D$ 与四边形 $A^{'} B^{'} C^{'} D^{'}$ 的面积比为 $2 ： 3$ ，则 $O A ： O A^{'} =$ （　　）

A、 $2 ： 3$ B、 $4 ： 9$ C、 $2 ： 5$ D、 $\sqrt{2} ： \sqrt{3}$

查看试题解析
6. 若锐角A满足 $s i n A = c o s 35 °$ ，则 $∠ A$ 的度数是（　　）

A、 $65 °$ B、 $55 °$ C、 $45 °$ D、 $35 °$

查看试题解析
7. 在 $R t △ A B C$ 中， $∠ C = 90 °$ ，若 $△ A B C$ 的三边都扩大2023倍，则 $t a n B$ 的值（　　）

A、不变 B、缩小2023倍 C、扩大2023倍 D、扩大 $\frac{1}{2023}$ 倍

查看试题解析
8. 如图，以点O为圆心，任意长为半径画弧，与射线 $O A$ 交于点B，再以点B为圆心， $B O$ 长为半径画弧，若两弧交于点C，画射线 $O C$ ，则 $t a n ∠ A O C$ 的值为（　　）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{3}}{3}$ C、 $\frac{\sqrt{2}}{2}$ D、 $\sqrt{3}$

查看试题解析
9. 如图， $△ A B C$ 的顶点在格点（网格线的交点）上，则 $c o s B$ 的值为（　　）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{\sqrt{3}}{2}$ D、1

查看试题解析
10. 如图，正方形 $A B C D$ 位于第一象限， $A C = 2 \sqrt{2}$ ，顶点A，C在直线 $y = x$ 上，且点A的横坐标为1，若双曲线 $y = \frac{k}{x} (k \neq 0)$ 与正方形 $A B C D$ 有两个交点，则k的取值范围是（　　）

A、 $0 < k < 1$ 或 $k > 6$ B、 $1 < k < 6$ C、 $1 < k < 9$ D、 $0 < k \leq 1$ 或 $k > 9$

查看试题解析

二、填空题

11. 在 $R t △ A B C$ 中，若 $∠ C = 90 ° ， A C = 4 ， A B = 5$ ，则 $t a n B =$

查看试题解析
12. 如图，将一个Rt△ABC形状的楔子从木桩的底点P沿水平方向打入木桩底下，使木桩向上移动．已知楔子斜面的倾斜角为15°，若楔子沿水平方向前进6cm（如箭头所示），则木桩上升了 .（结果可含有三角函数）

查看试题解析
13. 已知二次函数 $y = - x^{2} + 2 x$ ，当 $- 1 < x < a$ 时，y随x的增大而增大，则实数a的取值范围是

查看试题解析
14. 如图，小红同学正在使用手电筒进行物理光学实验，地面上从左往右依次是墙、木板和平面镜．手电筒的灯泡在点G处，手电筒的光从平面镜上点B处反射后，恰好经过木板的边缘点F，落在墙上的点E处．点E到地面的高度 $D E = 3.5 m$ ，点F到地面的高度 $C F = 1.5 m$ ，灯泡到木板的水平距离 $A C = 5.4 m$ ，墙到木板的水平距离为 $C D = 4 m$ ．已知 $∠ A B G = ∠ C B F$ ，图中点A，B，C，D在同一水平面上．

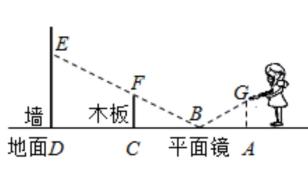(1)、 $B C$ 的长为

(2)、灯泡到地面的高度 $A G$ 为

查看试题解析

三、解答题

15. 计算∶ $3 t a n 30 ° - t a n 45 ° ＋ 2 s i n 60 ° - 4 c o s 30 °$ ．

查看试题解析
16. 如图，在平面直角坐标系中， $△ A B C$ 的三个顶点坐标分别为 $A (- 2 ， 1)$ ， $B (- 1 ， 4)$ ， $C (- 3 ， 2)$ ．

( 1 )画出 $△ A B C$ 关于y轴对称的图形 $△ A_{1} B_{1} C_{1}$ ；

( 2 )以原点O为位似中心，位似比为 $2 ： 1$ ，在y轴的左侧，画出 $△ A B C$ 放大后的图形 $△ A_{2} B_{2} C_{2}$ ，并直接写出 $C_{2}$ 点坐标．

查看试题解析
17. 如图，在 $△ A B C$ 中， $A D ⊥ B C$ 于点D， $c o s B = \frac{4}{5}$ ， $t a n C = \sqrt{3}$ ， $A B = 5$ ，求 $A C$ 的长．

查看试题解析
18. 已知在平面直角坐标系 $x O y$ 中，一次函数 $y = - x + 4$ 的图象与反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象相交于点 $A (- 1 ， m)$ ．

(1)、求反比例函数的表达式．

(2)、若点 $C (x ， y)$ 也在反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象上，当 $1 < x < 6$ 时，求y的取值范围．

查看试题解析
19. 如图， $∠ M O N = 45 °$ ，在 $∠ M O N$ 内部作以点O为位似中心的正方形 $A_{1} B_{1} C_{1} A_{2}$ ，正方形 $A_{2} B_{2} C_{2} A_{3}$ ，正方形 $A_{3} B_{3} C_{3} A_{4}$ ， …，正方形 $A_{n} B_{n} C_{n} A_{n + 1}$ ，其对应顶点 $A_{1} ， A_{2} ， A_{3} ， ⋯ ， A_{n}$ ，都在射线 $O N$ 上，对应顶点 $B_{1} ， B_{2} ， B_{3} ， ⋯ ， B_{n}$ ，都在射线 $O M$ 上，将正方形 $A_{1} B_{1} C_{1} A_{2}$ 的面积记作 $S_{1}$ ，正方形 $A_{2} B_{2} C_{2} A_{3}$ 的面积记作 $S_{2}$ ，正方形 $A_{3} B_{3} C_{3} A_{4}$ 的面积记作 $S_{3}$ ， …，依此类推，正方形 $A_{n} B_{n} C_{n} A_{n + 1}$ 的面积记作 $S_{n}$ ， $A_{1} B_{1} = 1$ ．

(1)、第5个正方形的面积 $S_{5} =$

(2)、第 n个正方形的面积 $S_{n} =$

(3)、若正方形的面积为 $2^{20}$ ，则这是第几个正方形？

查看试题解析
20. 如图，抛物线 $y = - x^{2} + 2 x + m + 1$ 交x轴于点 $A (a ， 0)$ 和 $B (b ， 0)$ ，交y轴于点C，抛物线的顶点为D．

(1)、当 $a = - 1$ 时，求b的值．

(2)、抛物线上有两点 $P (x_{1} ， y_{1})$ 和 $Q (x_{2} ， y_{2})$ ，若 $x_{1} < 1 < x_{2}$ ，且 $x_{1} + x_{2} > 2$ ，比较 $y_{1} ， y_{2}$ 的大小关系．

查看试题解析
21. 某地下车库出口处安装了“两段式栏杆”，如图1，A是栏杆转动的支点，E是栏杆两段的联结点．当车辆经过时，栏杆 $A E F$ 最多只能升起到如图2所示的位置，其示意图如图3所示（栏杆宽度忽略不计），其中 $A B ⊥ B C$ ， $E F ∥ B C$ ， $∠ A E F = 143 °$ ， $A B = A E = 1.2 m$ ，求此时杆 $E F$ 到地面 $B C$ 的距离．（参考数据∶ $s i n 37 ° \approx 0.60$ ， $c o s 37 ° \approx 0.80$ ， $t a n 37 ° \approx 0.75$ ）

查看试题解析
22. 如图，在 $△ A B D$ 中，C为 $A D$ 上一点，且 $A D = 4 C D$ ， $∠ C B D = ∠ A$ ，过点D作 $D H ∥ A B$ ，交 $B C$ 的延长线于点H．

(1)、求证∶ $△ H C D ∽ △ H D B$ ．

(2)、若 $B C = 6$ ，求 $D H$ 的长度．

查看试题解析
23. 如图，在正方形 $A B C D$ 中， $△ B P C$ 是等边三角形， $B P ， C P$ 的延长线分别交 $A D$ 于点E，F，连接 $B D ， D P$ ， $B D$ 与 $C F$ 相交于点H．

(1)、求证∶ $△ B D E ∽ △ D P E$ ．

(2)、求 $\frac{F P}{P H}$ 的值

(3)、求 $t a n ∠ D B E$ 的值．

查看试题解析