2022~2023学年中考数学一轮复习专题19二次函数综合问题(压轴)
试卷更新日期:2022-12-14 类型:一轮复习
一、含参问题
-
1. 已知抛物线的图象与轴交于点、 , 若以为直径的圆与在轴下方的抛物线有交点,则的取值范围是( )A、 B、 C、 D、2. 在平面直角坐标系中,若点的横坐标和纵坐标相等,则称点为完美点已知二次函数的图象上有且只有一个完美点 , 且当时,函数的最小值为 , 最大值为 , 则的取值范围是( )A、 B、 C、 D、3. 已知二次函数y=﹣x2+4x+5及一次函数y=﹣x+b,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新图象(如图所示),当直线y=﹣x+b与新图象有4个交点时,b的取值范围是 .
 4. 已知二次函数 , 当时,y的最小值为 , 则a的值为( )A、或4 B、或 C、或4 D、或45. 若二次函数的图象上有且只有三个点到x轴的距离等于m,则m的值为 .6. 已知二次函数 , 图象的一部分如图所示,该函数图象经过点 , 对称轴为直线.对于下列结论:①;②;③;④(其中);⑤若和均在该函数图象上,且 , 则.其中正确结论的个数共有个.
4. 已知二次函数 , 当时,y的最小值为 , 则a的值为( )A、或4 B、或 C、或4 D、或45. 若二次函数的图象上有且只有三个点到x轴的距离等于m,则m的值为 .6. 已知二次函数 , 图象的一部分如图所示,该函数图象经过点 , 对称轴为直线.对于下列结论:①;②;③;④(其中);⑤若和均在该函数图象上,且 , 则.其中正确结论的个数共有个. 7. 已知直线l:经过点(0,7)和点(1,6).(1)、求直线l的解析式;(2)、若点P(m,n)在直线l上,以P为顶点的抛物线G过点(0,-3),且开口向下
7. 已知直线l:经过点(0,7)和点(1,6).(1)、求直线l的解析式;(2)、若点P(m,n)在直线l上,以P为顶点的抛物线G过点(0,-3),且开口向下①求m的取值范围;
②设抛物线G与直线l的另一个交点为Q,当点Q向左平移1个单长度后得到的点Q' 也在G上时,求G在≤≤的图象的最高点的坐标.
8. 已知:经过点 , .(1)、求函数解析式;(2)、平移抛物线使得新顶点为(m>0).①倘若 , 且在的右侧,两抛物线都上升,求的取值范围;
②在原抛物线上,新抛物线与轴交于 , 时,求点坐标.
9. 已知二次函数 , 当时,函数值y的最小值为1,则a的值为 .10. 如图,抛物线与轴交于 , 两点,与轴交于点 , 连接 .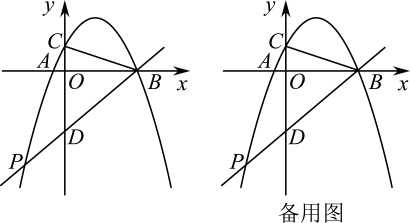 (1)、求抛物线的解析式.(2)、点是第三象限抛物线上一点,直线与轴交于点 , 的面积为12,求点的坐标.(3)、在(2)的条件下,若点是线段上点,连接 , 将沿直线翻折得到 , 当直线与直线相交所成锐角为时,求点的坐标.11. 已知二次函数y=ax2+4ax+3a(a为常数).(1)、若二次函数的图象经过点(2,3),求函数y的表达式,:(2)、若a>0,当x<时,此二次函数y随着x的增大而减小,求m的取值范围,(3)、若二次函数在-3≤x≤1时有最大值3,求a的值.
(1)、求抛物线的解析式.(2)、点是第三象限抛物线上一点,直线与轴交于点 , 的面积为12,求点的坐标.(3)、在(2)的条件下,若点是线段上点,连接 , 将沿直线翻折得到 , 当直线与直线相交所成锐角为时,求点的坐标.11. 已知二次函数y=ax2+4ax+3a(a为常数).(1)、若二次函数的图象经过点(2,3),求函数y的表达式,:(2)、若a>0,当x<时,此二次函数y随着x的增大而减小,求m的取值范围,(3)、若二次函数在-3≤x≤1时有最大值3,求a的值.二、抛物线型问题
-
12. 如图1为北京冬奥会“雪飞天”滑雪大跳台赛道的横截面示意图.取水平线OE为x轴,铅垂线OD为y轴,建立平面直角坐标系.运动员以速度从D点滑出,运动轨迹近似抛物线 . 某运动员7次试跳的轨迹如图2.在着陆坡CE上设置点K(与DO相距32m)作为标准点,着陆点在K点或超过K点视为成绩达标.
(参考数据: , )
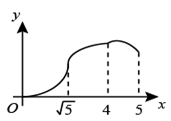
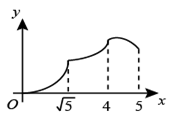
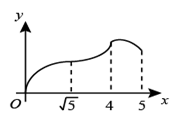
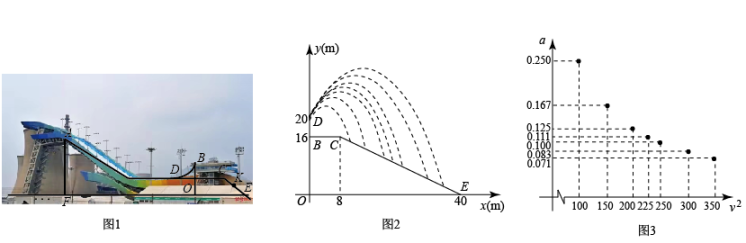 (1)、求线段CE的函数表达式(写出的取值范围).(2)、当时,着陆点为P,求P的横坐标并判断成绩是否达标.(3)、在试跳中发现运动轨迹与滑出速度v的大小有关,进一步探究,测算得7组a与 的对应数据,在平面直角坐标系中描点如图3.
(1)、求线段CE的函数表达式(写出的取值范围).(2)、当时,着陆点为P,求P的横坐标并判断成绩是否达标.(3)、在试跳中发现运动轨迹与滑出速度v的大小有关,进一步探究,测算得7组a与 的对应数据,在平面直角坐标系中描点如图3.①猜想a关于的函数类型,求函数表达式,并任选一对对应值验证.
②当v为多少m/s时,运动员的成绩恰能达标(精确到1m/s)?
13. 在北京冬奥会自由式滑雪大跳台比赛中,我国选手谷爱凌的精彩表现让人叹为观止,已知谷爱凌从2m高的跳台滑出后的运动路线是一条抛物线,设她与跳台边缘的水平距离为xm,与跳台底部所在水平面的竖直高度为ym,y与x的函数关系式为y=x2+x+2(0≤x≤20.5),当她与跳台边缘的水平距离为m时,竖直高度达到最大值.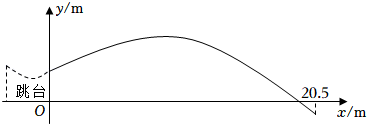
三、函数应用最值问题
-
14. 在平面直角坐标系xOy中,已知抛物线y=-x2+2mx+3m,点A(3,0).
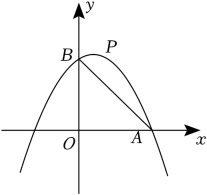 (1)、当抛物线过点A时,求抛物线的解析式;(2)、证明:无论m为何值,抛物线必过定点D,并求出点D的坐标;(3)、在(1)的条件下,抛物线与y轴交于点B,点P是抛物线上位于第一象限的点,连接AB,PD交于点M,PD与y轴交于点N.设S=S△PAM-S△BMN,问是否存在这样的点P,使得S有最大值?若存在,请求出点P的坐标,并求出S的最大值;若不存在,请说明理由.15. 如图,在平面直角坐标系中,抛物线与x轴分别交于点A(1,0)和点B,与y轴交于点C(0,﹣3),连接BC.
(1)、当抛物线过点A时,求抛物线的解析式;(2)、证明:无论m为何值,抛物线必过定点D,并求出点D的坐标;(3)、在(1)的条件下,抛物线与y轴交于点B,点P是抛物线上位于第一象限的点,连接AB,PD交于点M,PD与y轴交于点N.设S=S△PAM-S△BMN,问是否存在这样的点P,使得S有最大值?若存在,请求出点P的坐标,并求出S的最大值;若不存在,请说明理由.15. 如图,在平面直角坐标系中,抛物线与x轴分别交于点A(1,0)和点B,与y轴交于点C(0,﹣3),连接BC.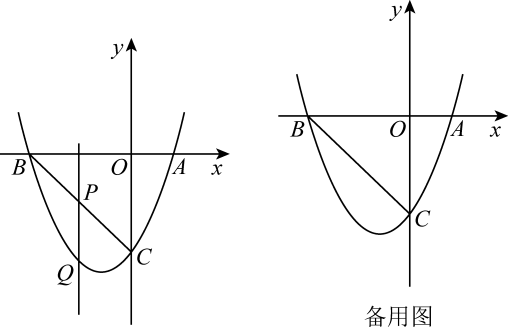 (1)、求抛物线的解析式及点B的坐标.(2)、如图,点P为线段BC上的一个动点(点P不与点B,C重合),过点P作y轴的平行线交抛物线于点Q,求线段PQ长度的最大值.(3)、动点P以每秒个单位长度的速度在线段BC上由点C向点B运动,同时动点M以每秒1个单位长度的速度在线段BO上由点B向点O运动,在平面内是否存在点N,使得以点P,M,B,N为顶点的四边形是菱形?若存在,请直接写出符合条件的点N的坐标;若不存在,请说明理由.16. 如图,在平面直角坐标系中,抛物线(a≠0)的图象与x轴交于A、C两点,与y轴交于点B,其中点B坐标为(0,-4),点C坐标为(2,0).
(1)、求抛物线的解析式及点B的坐标.(2)、如图,点P为线段BC上的一个动点(点P不与点B,C重合),过点P作y轴的平行线交抛物线于点Q,求线段PQ长度的最大值.(3)、动点P以每秒个单位长度的速度在线段BC上由点C向点B运动,同时动点M以每秒1个单位长度的速度在线段BO上由点B向点O运动,在平面内是否存在点N,使得以点P,M,B,N为顶点的四边形是菱形?若存在,请直接写出符合条件的点N的坐标;若不存在,请说明理由.16. 如图,在平面直角坐标系中,抛物线(a≠0)的图象与x轴交于A、C两点,与y轴交于点B,其中点B坐标为(0,-4),点C坐标为(2,0).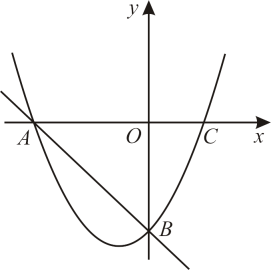 (1)、求此抛物线的函数解析式.(2)、点D是直线AB下方抛物线上一个动点,连接AD、BD,探究是否存在点D,使得△ABD的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由.(3)、点P为该抛物线对称轴上的动点,使得△PAB为直角三角形,请求出点P的坐标.17. 已知抛物线与x轴交于两点(A左B右),交y轴负半轴点C,P是第四象限抛物线上一点.
(1)、求此抛物线的函数解析式.(2)、点D是直线AB下方抛物线上一个动点,连接AD、BD,探究是否存在点D,使得△ABD的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由.(3)、点P为该抛物线对称轴上的动点,使得△PAB为直角三角形,请求出点P的坐标.17. 已知抛物线与x轴交于两点(A左B右),交y轴负半轴点C,P是第四象限抛物线上一点. (1)、若 , 求a的值;(2)、若 , 过点P作直线垂直于x轴,交于点Q,求线段的最大值,并求此时点P的坐标;(3)、直线交y轴于点M,直线交y轴于点N,求的值.
(1)、若 , 求a的值;(2)、若 , 过点P作直线垂直于x轴,交于点Q,求线段的最大值,并求此时点P的坐标;(3)、直线交y轴于点M,直线交y轴于点N,求的值.四、特殊三角形存在性问题
-
18. 如图,抛物线与x轴交于点 , 点 , 与y轴交于点C.
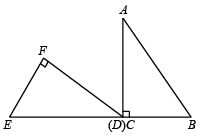
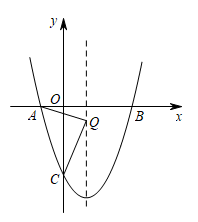 (1)、求抛物线的表达式;(2)、在对称轴上找一点Q,使的周长最小,求点Q的坐标;(3)、点P是抛物线对称轴上的一点,点M是对称轴左侧抛物线上的一点,当是以为腰的等腰直角三角形时,请直接写出所有点M的坐标.19. 如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点B.抛物线过A,B两点,与x轴的另一个交点为C, .
(1)、求抛物线的表达式;(2)、在对称轴上找一点Q,使的周长最小,求点Q的坐标;(3)、点P是抛物线对称轴上的一点,点M是对称轴左侧抛物线上的一点,当是以为腰的等腰直角三角形时,请直接写出所有点M的坐标.19. 如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点B.抛物线过A,B两点,与x轴的另一个交点为C, .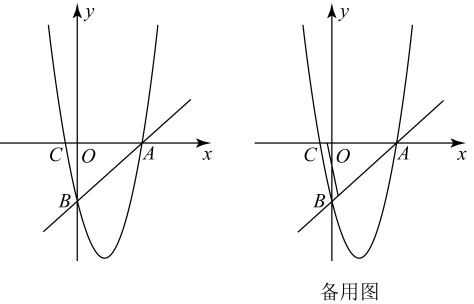 (1)、求抛物线的表达式;(2)、若点P为抛物线的顶点,求四边形的面积;(3)、抛物线上是否存在点Q,使得是以为直角边的直角三角形?若存在,求出点Q的坐标;若不存在,说明理由.
(1)、求抛物线的表达式;(2)、若点P为抛物线的顶点,求四边形的面积;(3)、抛物线上是否存在点Q,使得是以为直角边的直角三角形?若存在,求出点Q的坐标;若不存在,说明理由.五、特殊四边形存在性问题
-
20. 如图,在平面直角坐标系中,经过点的直线AB与y轴交于点 . 经过原点O的抛物线交直线AB于点A,C,抛物线的顶点为D.
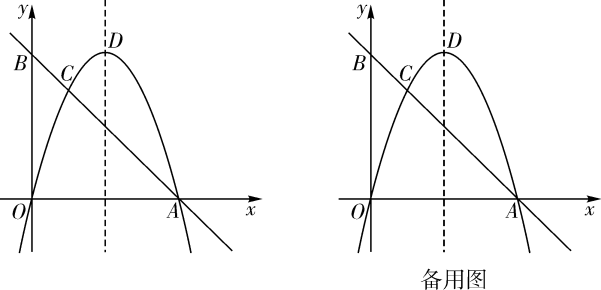 (1)、求抛物线的表达式;(2)、M是线段AB上一点,N是抛物线上一点,当轴且时,求点M的坐标;(3)、P是抛物线上一动点,Q是平面直角坐标系内一点.是否存在以点A,C,P,Q为顶点的四边形是矩形?若存在,直接写出点Q的坐标;若不存在,请说明理由.21. 已知抛物线与x轴有公共点.
(1)、求抛物线的表达式;(2)、M是线段AB上一点,N是抛物线上一点,当轴且时,求点M的坐标;(3)、P是抛物线上一动点,Q是平面直角坐标系内一点.是否存在以点A,C,P,Q为顶点的四边形是矩形?若存在,直接写出点Q的坐标;若不存在,请说明理由.21. 已知抛物线与x轴有公共点.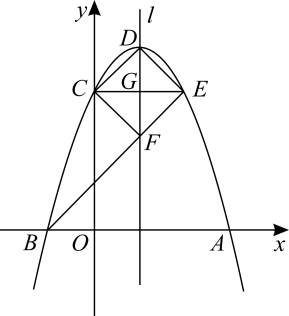 (1)、当y随x的增大而增大时,求自变量x的取值范围;(2)、将抛物线先向上平移4个单位长度,再向右平移n个单位长度得到抛物线(如图所示),抛物线与x轴交于点A,B(点A在点B的右侧),与y轴交于点C.当OC=OA时,求n的值;(3)、D为抛物线的顶点,过点C作抛物线的对称轴l的垂线,垂足为G,交抛物线于点E,连接BE交l于点F.求证:四边形CDEF是正方形.22. 如图,在平面直角坐标系中,经过点A(4,0)的直线AB与y轴交于点B(0,4).经过原点O的抛物线y=-x2+bx+c交直线AB于点A,C,抛物线的顶点为D.
(1)、当y随x的增大而增大时,求自变量x的取值范围;(2)、将抛物线先向上平移4个单位长度,再向右平移n个单位长度得到抛物线(如图所示),抛物线与x轴交于点A,B(点A在点B的右侧),与y轴交于点C.当OC=OA时,求n的值;(3)、D为抛物线的顶点,过点C作抛物线的对称轴l的垂线,垂足为G,交抛物线于点E,连接BE交l于点F.求证:四边形CDEF是正方形.22. 如图,在平面直角坐标系中,经过点A(4,0)的直线AB与y轴交于点B(0,4).经过原点O的抛物线y=-x2+bx+c交直线AB于点A,C,抛物线的顶点为D. (1)、求抛物线y=-x2+bx+c的表达式;(2)、M是线段AB上一点,N是抛物线上一点,当MN∥y轴且MN=2时,求点M的坐标;(3)、P是抛物线上一动点,Q是平面直角坐标系内一点.是否存在以点A,C,P,Q为顶点的四边形是矩形?若存在,直接写出点Q的坐标;若不存在,请说明理由.23. 如图, 拋物线交y轴于点 , 交x轴于点、C两点,点D为线段上的一个动点(不与重合),过点D作轴,交于点M,交抛物线于点N.
(1)、求抛物线y=-x2+bx+c的表达式;(2)、M是线段AB上一点,N是抛物线上一点,当MN∥y轴且MN=2时,求点M的坐标;(3)、P是抛物线上一动点,Q是平面直角坐标系内一点.是否存在以点A,C,P,Q为顶点的四边形是矩形?若存在,直接写出点Q的坐标;若不存在,请说明理由.23. 如图, 拋物线交y轴于点 , 交x轴于点、C两点,点D为线段上的一个动点(不与重合),过点D作轴,交于点M,交抛物线于点N. (1)、求抛物线的解析式;(2)、连接和 , 当的面积最大时,求出点D的坐标及的最大面积;(3)、在平面内是否存在一点P,使得以点A,M,N,P为顶点,以为边的四边形是菱形?若存在,请求出点P的坐标;若不存在,请说明理由.24. 如图,在平面直角坐标系中,抛物线y=ax2+bx+2经过A( , 0),B(3,)两点,与y轴交于点C.
(1)、求抛物线的解析式;(2)、连接和 , 当的面积最大时,求出点D的坐标及的最大面积;(3)、在平面内是否存在一点P,使得以点A,M,N,P为顶点,以为边的四边形是菱形?若存在,请求出点P的坐标;若不存在,请说明理由.24. 如图,在平面直角坐标系中,抛物线y=ax2+bx+2经过A( , 0),B(3,)两点,与y轴交于点C.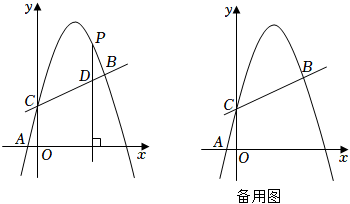 (1)、求抛物线的解析式;(2)、点P在抛物线上,过P作PD⊥x轴,交直线BC于点D,若以P、D、O、C为顶点的四边形是平行四边形,求点P的横坐标;(3)、抛物线上是否存在点Q,使∠QCB=45°?若存在,请直接写出点Q的坐标;若不存在,请说明理由.25. 如图,抛物线与x轴交于两点,与y轴交于点 , 连接AC、BC.
(1)、求抛物线的解析式;(2)、点P在抛物线上,过P作PD⊥x轴,交直线BC于点D,若以P、D、O、C为顶点的四边形是平行四边形,求点P的横坐标;(3)、抛物线上是否存在点Q,使∠QCB=45°?若存在,请直接写出点Q的坐标;若不存在,请说明理由.25. 如图,抛物线与x轴交于两点,与y轴交于点 , 连接AC、BC.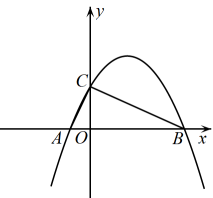
 (1)、求抛物线的表达式;(2)、将沿AC所在直线折叠,得到 , 点B的对应点为D,直接写出点D的坐标.并求出四边形OADC的面积;(3)、点P是抛物线上的一动点,当时,求点P的坐标.26. 在平面直角坐标系中,抛物线(b是常数)经过点 . 点A在抛物线上,且点A的横坐标为m().以点A为中心,构造正方形 , , 且轴.(1)、求该抛物线对应的函数表达式:(2)、若点B是抛物线上一点,且在抛物线对称轴左侧.过点B作x轴的平行线交抛物线于另一点C,连接 . 当时,求点B的坐标;(3)、若 , 当抛物线在正方形内部的点的纵坐标y随x的增大而增大时,或者y随x的增大而减小时,求m的取值范围;(4)、当抛物线与正方形的边只有2个交点,且交点的纵坐标之差为时,直接写出m的值.27. 如图,已知直线y=x+4与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c经过A,C两点,且与x轴的另一个交点为B,对称轴为直线x=﹣1.
(1)、求抛物线的表达式;(2)、将沿AC所在直线折叠,得到 , 点B的对应点为D,直接写出点D的坐标.并求出四边形OADC的面积;(3)、点P是抛物线上的一动点,当时,求点P的坐标.26. 在平面直角坐标系中,抛物线(b是常数)经过点 . 点A在抛物线上,且点A的横坐标为m().以点A为中心,构造正方形 , , 且轴.(1)、求该抛物线对应的函数表达式:(2)、若点B是抛物线上一点,且在抛物线对称轴左侧.过点B作x轴的平行线交抛物线于另一点C,连接 . 当时,求点B的坐标;(3)、若 , 当抛物线在正方形内部的点的纵坐标y随x的增大而增大时,或者y随x的增大而减小时,求m的取值范围;(4)、当抛物线与正方形的边只有2个交点,且交点的纵坐标之差为时,直接写出m的值.27. 如图,已知直线y=x+4与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c经过A,C两点,且与x轴的另一个交点为B,对称轴为直线x=﹣1.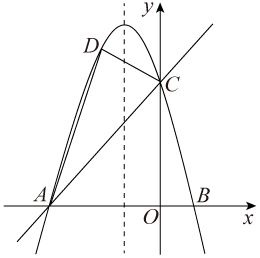 (1)、求抛物线的表达式;(2)、D是第二象限内抛物线上的动点,设点D的横坐标为m,求四边形ABCD面积S的最大值及此时D点的坐标;(3)、若点P在抛物线对称轴上,是否存在点P,Q,使以点A,C,P,Q为顶点的四边形是以AC为对角线的菱形?若存在,请求出P,Q两点的坐标;若不存在,请说明理由.
(1)、求抛物线的表达式;(2)、D是第二象限内抛物线上的动点,设点D的横坐标为m,求四边形ABCD面积S的最大值及此时D点的坐标;(3)、若点P在抛物线对称轴上,是否存在点P,Q,使以点A,C,P,Q为顶点的四边形是以AC为对角线的菱形?若存在,请求出P,Q两点的坐标;若不存在,请说明理由.六、函数图象问题
-
28. 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+c和反比例函数y=在同一平面直角坐标系中的图象可能是( )
 A、
A、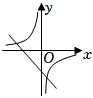 B、
B、 C、
C、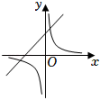 D、
D、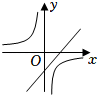 29. 二次函数 的大致图象如图所示,顶点坐标为 , 下列结论: ①; ②;③;④若方程有两个根和 , 且 , 则; ⑤若方程有四个根,则这四个根的和为 , 其中正确的结论有( )
29. 二次函数 的大致图象如图所示,顶点坐标为 , 下列结论: ①; ②;③;④若方程有两个根和 , 且 , 则; ⑤若方程有四个根,则这四个根的和为 , 其中正确的结论有( ) A、①②③ B、①②⑤ C、②③④⑤ D、①②④⑤30. 已知抛物线(),且 , . 给出下列结论:
A、①②③ B、①②⑤ C、②③④⑤ D、①②④⑤30. 已知抛物线(),且 , . 给出下列结论:①;②;③抛物线与轴正半轴必有一个交点;④当时,;⑤该抛物线与直线有两个交点.其中正确结论的个数为( )
A、2个 B、3个 C、4个 D、5个31. 如图,抛物线交x轴于点和 , 交y轴于点C.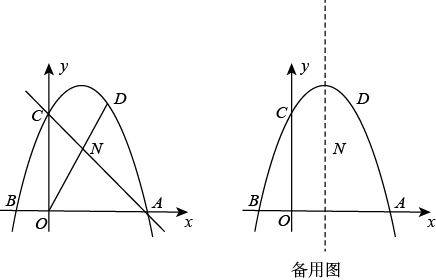 (1)、求抛物线的表达式;(2)、D是直线上方抛物线上一动点,连接交于点N,当的值最大时,求点D的坐标;(3)、P为抛物线上一点,连接 , 过点P作交抛物线对称轴于点Q,当时,请直接写出点P的横坐标.
(1)、求抛物线的表达式;(2)、D是直线上方抛物线上一动点,连接交于点N,当的值最大时,求点D的坐标;(3)、P为抛物线上一点,连接 , 过点P作交抛物线对称轴于点Q,当时,请直接写出点P的横坐标.