湖南省益阳市2022-2023学年高二上学期数学12月大联考试卷

试卷更新日期：2022-12-14 类型：月考试卷

进入出卷网下载

一、单选题

1. 已知两点 $A (0 ， 2 ， 3)$ ， $B (1 ， 0 ， - 1)$ ，则 $| \vec{A B} | =$ （）

A、 $\sqrt{13}$ B、 $\sqrt{14}$ C、 $2 \sqrt{5}$ D、 $\sqrt{21}$

查看试题解析
2. 若直线 $a x - 2 y - 3 = 0$ 与 $a x + 2 y - 1 = 0$ 垂直，则 $a$ 的值为（）

A、 $- 2$ B、 $2$ C、 $- 2$ 或 $2$ D、 $0$

查看试题解析
3. 已知i为虚数单位，则复数 $(1 - i) (2 - i) =$ （）

A、 $- 1 - 3 i$ B、 $- 1 + 3 i$ C、 $1 - 3 i$ D、 $1 + 3 i$

查看试题解析
4. 设等比数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ， $S_{8} = 3 S_{4}$ ，则 $\frac{a_{6} + a_{8}}{a_{2} + a_{4}}$ 的值为（）

A、 $2$ B、 $2 \sqrt{2}$ C、 $4$ D、 $4 \sqrt{2}$

查看试题解析
5. 已知正方形 $A B C D$ ，以 $A$ ， $C$ 两点为焦点的椭圆恰好过正方形四边的中点，则椭圆的离心率为（）

A、 $\frac{\sqrt{2}}{2}$ B、 $\frac{\sqrt{5} - 1}{2}$ C、 $\frac{\sqrt{10} - \sqrt{2}}{2}$ D、 $\frac{\sqrt{5}}{3}$

查看试题解析
6. 南宋数学家在 $《$ 详解九章算法 $》$ 和 $《$ 算法通变本末 $》$ 中提出了一些新的垛积公式，所讨论的二阶等差数列与一般等差数列不同，二阶等差数中前后两项之差并不相等，但是逐项之差成等差数列．现有二阶等差数列，其前 $7$ 项分别为 $1$ ， $2$ ， $5$ ， $10$ ， $17$ ， $26$ ， $37$ ，则该数列的第 $20$ 项为（）

A、 $324$ B、 $325$ C、 $362$ D、 $399$

查看试题解析
7. 已知实数 $x$ ， $y$ 满足 $4 x^{2} + y^{2} + x y = 1$ ，且不等式 $2 x + y - t < 0$ 恒成立，则实数 $t$ 的取值范围为（）

A、 $t > \frac{5}{8}$ B、 $t > \frac{2 \sqrt{10}}{5}$ C、 $t > \frac{\sqrt{10}}{4}$ D、 $t > \frac{8}{5}$

查看试题解析
8. 在平面直角坐标系 $x O y$ 中，已知圆 $O_{1} ： x^{2} + y^{2} = 1$ ， $O_{2} ： (x - 4)^{2} + y^{2} = 4$ ，动点 $P$ 在直线x+ $\sqrt{3} y$ -b=0上，过 $P$ 点分别作圆 $O_{1}$ ， $O_{2}$ 的切线，切点分别为 $A$ ， $B$ ，若存在点 $P$ 满足 $P B = 2 P A$ ，则实数 $b$ 的取值范围是（）

A、 $[- 12 ， \frac{28}{3}]$ B、 $(- \infty ， - \frac{28}{3}] ∪ [12 ， + \infty)$ C、 $[- \frac{20}{3} ， 4]$ D、 $(- \infty ， - \frac{20}{3}] ∪ [4 ， + \infty)$

查看试题解析

二、多选题

9. 下列各式中，值为 $\frac{1}{2}$ 的是（）

A、 $s i n \frac{5 π}{6}$ B、 $2 s i n 15 ° c o s 15 °$ C、 $2 c o s^{2} 15 ° - 1$ D、 $\frac{\sqrt{3}}{2} t a n 210 °$

查看试题解析
10. 已知双曲线 $\frac{x^{2}}{9} - \frac{y^{2}}{16} = 1$ 的左、右焦点分别为 $F_{1}$ ， $F_{2}$ ，左、右顶点分别为 $A$ ， $B$ ，点 $P$ 在双曲线上（异于左右顶点），则下列结论正确的是（）

A、该双曲线的离心率为 $\frac{5}{3}$ B、若 $P F_{1} ⊥ F_{1} F_{2}$ ，则 $△ P F_{1} F_{2}$ 的面积为 $\frac{160}{3}$ C、点 $P$ 到两渐近线的距离乘积为 $\frac{144}{25}$ D、直线 $P A$ 和直线 $P B$ 的斜率乘积为 $\frac{16}{9}$

查看试题解析
11. 在矩形 $A B C D$ 中， $A B = 2 ， A D = 2 \sqrt{3}$ ，沿对角线 $A C$ 将矩形折成一个大小为 $θ$ 的二面角 $B - A C - D$ ，若 $c o s θ = \frac{1}{3}$ ，则下列各选项正确的是（）

A、四面体 $A B C D$ 外接球的表面积为 $16 π$ B、点B与点D之间的距离为 $2 \sqrt{3}$ C、四面体 $A B C D$ 的体积为 $\frac{4 \sqrt{2}}{3}$ D、异面直线 $A C$ 与 $B D$ 所成的角为 $45 °$

查看试题解析
12. 意大利著名数学家斐波那契在研究兔子的繁殖问题时，发现有这样的一列数： $1$ ， $1$ ， $2$ ， $3$ ， $5$ ， $8$ ， $⋯$ .该数列的特点如下：前两个数均为 $1$ ，从第三个数起，每一个数都等于它前面两个数的和.人们把这样的一列数组成的数列 ${F_{n}}$ 称为斐波那契数列，现将 ${F_{n}}$ 中的各项除以 $4$ 所得余数按原顺序构成的数列记为 ${M_{n}}$ ，则下列结论中正确的是（）

A、 $M_{2022} = 1$ B、 $M_{6 n - 2} = M_{6 n - 4} + 2 M_{6 n - 5} (n \geq 1 ， n \in N^{*})$ C、 $F_{1}^{2} + F_{2}^{2} + F_{3}^{2} + ⋯ + F_{2021}^{2} = F_{2021} F_{2022}$ D、 $F_{1} + F_{2} + F_{3} + ⋯ + F_{2021} = F_{2022} - 1$

查看试题解析

三、填空题

13. 圆 $O ： x^{2} + y^{2} = 4$ 和圆 $M ： x^{2} + y^{2} - 6 x - 2 y + 9 = 0$ 公切线的条数为．

查看试题解析
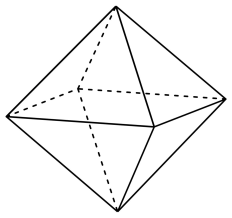
14. 点 $(- 1 ， 3)$ 关于直线 $x + y + 2 = 0$ 的对称点的坐标为．

查看试题解析
15. 六氟化硫，化学式为 $S F_{6}$ ，在常压下是一种无色､无臭､无毒､不燃的稳定气体，有良好的绝缘性，在电器工业方面具有广泛用途.六氟化硫分子结构为正八面体结构（正八面体是每个面都是正三角形的八面体），如图所示.若此正八面体的内切球的半径为 $\sqrt{6}$ ，则该正八面体的表面积为.

查看试题解析
16. 抛物线 $C ： y^{2} = 4 x$ 的焦点为 $F$ ，点 $D (2 ， 0)$ ，过 $F$ 的直线交抛物线 $C$ 于 $M$ ， $N$ 两点.设直线 $M D$ ， $N D$ 与抛物线 $C$ 的另一个交点分别为 $A$ ， $B$ .当直线 $M D$ 垂直于 $x$ 轴时， $| M F | =$ ；记直线 $M N$ ， $A B$ 的斜率分别为 $k_{1}$ ， $k_{2}$ ，则 $\frac{k_{1}}{k_{2}}$ 的值为.

查看试题解析

四、解答题

17. 在锐角 $△ A B C$ 中，内角 $A$ 、 $B$ 、 $C$ 所对的边分别为 $a$ ， $b$ ， $c$ ， $\vec{m} = (c o s A ， s i n A)$ ， $\vec{n} = (c o s A ， - s i n A)$ ，向量 $\vec{m}$ ， $\vec{n}$ 的夹角为 $\frac{2 π}{3}$ ．

(1)、求角 $A$ ；

(2)、若 $a = \frac{\sqrt{3}}{2}$ ，求 $△ A B C$ 周长的取值范围．

查看试题解析
18. 在平面直角坐标系中，已知圆 $C ： x^{2} + y^{2} - 2 y = 0$ ，直线 $l$ 的方程为 $x - 2 y + m = 0$ ，点 $A (- 1 ， 0)$ ．

(1)、若 $l$ 与圆 $C$ 相切，求 $m$ 的值；

(2)、若过点 $A$ 的直线 $l^{'}$ 截得圆 $C$ 的弦长 $| M N | \geq \sqrt{3}$ ，求 $l^{'}$ 的斜率的取值范围．

查看试题解析
19. 已知各项为正数的数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，若 $4 S_{n} = a_{n}^{2} + 2 a_{n} + 1$ .

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、设 $b_{n} = \frac{2}{a_{n} a_{n + 1}}$ ，且数列 ${b_{n}}$ 的前 $n$ 项和为 $T_{n}$ ，求证： $\frac{2}{3} \leq T_{n} < 1$ ．

查看试题解析
20. 在四棱锥 $A - B C D E$ 中，底面 $B C D E$ 为正方形，平面 $A D E ⊥$ 平面 $B C D E$ ， $A E = B E = 2$ ， $A D = 2 \sqrt{2}$ ， $M$ 是 $A B$ 的中点，点 $N$ 是线段 $B C$ 上靠近 $C$ 点的一个三等分点，

(1)、证明： $E M ⊥ A N$ ；

(2)、求二面角 $M - E N - B$ 的余弦值.

查看试题解析
21. 读书可以增长知识，开拓视野，修身怡情.树人中学为了解本校学生课外阅读情况，按性别进行分层，用分层随机抽样的方法从全校学生中抽出一个容量为100的样本，其中男生40名，女生60名.经调查统计，分别得到40名男生一周课外阅读时间（单位：小时）的频数分布表和60名女生一周课外阅读时间（单位：小时）的频率分布直方图.
男生一周阅读时间频数分布表
小时
频数
$[0 ， 2)$
9
$[2 ， 4)$
25
$[4 ， 6)$
3
$[6 ， 8)$
3

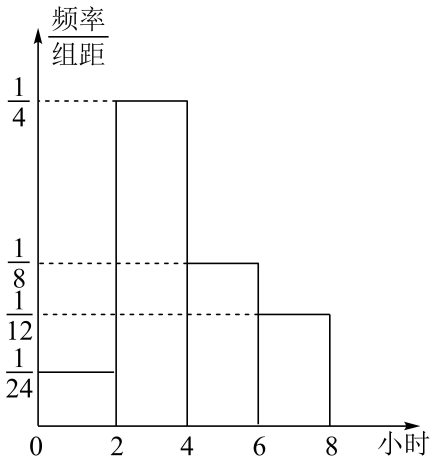(1)、由以上频率分布直方图估计该校女生一周阅读时间的众数和75%分位数；

(2)、由以上频数分布表和频率分布直方图估计总样本的平均数 $\bar{z}$ ；

(3)、从一周课外阅读时间为 $[4 ， 6)$ 的样本学生中按比例分配抽取6人，再从这6人中任意抽取2人，求恰好抽到一男一女的概率.
（注：以各组的区间中点值代表该组的各个值）

查看试题解析
22. 已知椭圆 $E ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的右焦点 $F$ 与上下顶点构成一个等腰直角三角形，且直线 $x + y + \sqrt{3} = 0$ 与椭圆 $E$ 仅有一个公共点．

(1)、求椭圆 $E$ 的方程；

(2)、斜率不为 $0$ 的直线 $l$ 过点 $F$ ，与椭圆 $E$ 交于 $A$ ， $B$ 两点，弦 $A B$ 的中点为 $H$ ， $O$ 为坐标原点，直线 $O H$ 与椭圆 $E$ 交于点 $M$ ， $N$ ，求四边形 $A M B N$ 面积 $S$ 的最小值．

查看试题解析

男生一周阅读时间频数分布表
小时	频数
$[0 ， 2)$	9
$[2 ， 4)$	25
$[4 ， 6)$	3
$[6 ， 8)$	3