湖北省十一校2023届高三上学期数学12月第一次联考试卷

试卷更新日期：2022-12-14 类型：月考试卷

进入出卷网下载

一、单选题

1. 集合 $P = {x \in R | y = l n (3 - x)} ， Q = {y \in R | y = 2^{x} ， x \in P}$ ，则 $P ∩ Q =$ （）

A、 $(- \infty ， 3)$ B、 $(0 ， 3)$ C、 $(1 ， 3)$ D、 $(- \infty ， 8)$

查看试题解析
2. 复数 $z$ 满足 $| z - 5 | = | z - 1 | = | z + i |$ ，则 $| z | =$ （）

A、 $\sqrt{10}$ B、 $\sqrt{13}$ C、 $3 \sqrt{2}$ D、5

查看试题解析
3. 随机掷两个质地均匀的正方体骰子，骰子各个面分别标记有 $1 \sim 6$ 共六个数字，记事件 $A =$ “骰子向上的点数是1和3”，事件 $B =$ “骰子向上的点数是3和6”，事件 $C =$ “骰子向上的点数含有3”，则下列说法正确的是（）

A、事件 $A$ 与事件 $B$ 是相互独立事件 B、事件 $A$ 与事件 $C$ 是互斥事件 C、 $P (A) = P (B) = \frac{1}{18}$ D、 $P (C) = \frac{1}{6}$

查看试题解析
4. 在平行四边形 $A B C D$ 中， $E$ ､ $F$ 分别在边 $A D$ ､ $C D$ 上， $A E = 3 E D$ ， $D F = F C ， A F$ 与 $B E$ 相交于点 $G$ ，记 $\vec{A B} = \vec{a} ， \vec{A D} = \vec{b}$ ，则 $\vec{A G} =$ （）

A、 $\frac{3}{11} \vec{a} + \frac{4}{11} \vec{b}$ B、 $\frac{6}{11} \vec{a} + \frac{3}{11} \vec{b}$ C、 $\frac{4}{11} \vec{a} + \frac{5}{11} \vec{b}$ D、 $\frac{3}{11} \vec{a} + \frac{6}{11} \vec{b}$

查看试题解析
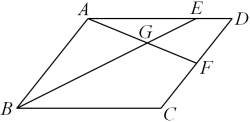5. 则三棱锥 $P - A B C$ 中， $P A ⊥$ 平面 $A B C ， P A = 6 ， B C = 3 ， ∠ C A B = \frac{π}{6}$ ，则三棱锥 $P - A B C$ 的外接球半径为（）

A、3 B、 $3 \sqrt{2}$ C、 $3 \sqrt{3}$ D、6

查看试题解析
6. 已知函数 $f (x) = s i n (ω x + \frac{π}{6})$ 在 $(0 ， \frac{π}{3})$ 上恰好取到一次最大值与一次最小值，则 $ω$ 的取值范围是（）

A、 $(4 ， 7]$ B、 $[4 ， 7)$ C、 $(7 ， 10]$ D、 $[7 ， 10)$

查看试题解析
7. 意大利数学家斐波那契以兔子繁殖数量为例，引入数列： $1 ， 1 ， 2 ， 3 ， 5 ， 8 ， \dots$ ，该数列从第三项起，每一项都等于前两项的和，即递推关系式为 $a_{n + 2} = a_{n + 1} + a_{n} ， n \in N^{*}$ ，故此数列称为斐波那契数列，又称“兔子数列”.已知满足上述递推关系式的数列 ${a_{n}}$ 的通项公式为 $a_{n} = A \cdot {(\frac{1 + \sqrt{5}}{2})}^{n} + B \cdot {(\frac{1 - \sqrt{5}}{2})}^{n}$ ，其中 $A ， B$ 的值可由 $a_{1}$ 和 $a_{2}$ 得到，比如兔子数列中 $a_{1} = 1 ， a_{2} = 1$ 代入解得 $A = \frac{1}{\sqrt{5}} ， B = - \frac{1}{\sqrt{5}}$ .利用以上信息计算 $[{(\frac{\sqrt{5} + 1}{2})}^{5}] = () . ([x]$ 表示不超过 $x$ 的最大整数 $)$ （）

A、10 B、11 C、12 D、13

查看试题解析
8. 已知 $a = \frac{1}{e l n \sqrt{2}} ， b = \frac{2}{\sqrt{e}} ， c = \frac{3 \sqrt[3]{e}}{4}$ （其中 $e$ 为自然常数），则 $a$ ､ $b$ ､ $c$ 的大小关系为（）

A、 $a < c < b$ B、 $b < a < c$ C、 $c < b < a$ D、 $c < a < b$

查看试题解析

二、多选题

9. 某校为了解学生每个月在图书馆借阅书籍的数量，图书管理员甲抽取了一个容量为100的样本，并算得样本的平均数为5，方差为9；图书管理员乙也抽取了一个容量为100的样本，并算得样本的平均数为7，方差为16.若将两个样本合在一起组成一个容量为200的新样本，则新样本数据的（）

A、平均数为6 B、平均数为 $6.5$ C、方差为 $12.5$ D、方差为 $13.5$

查看试题解析
10. 如图，在边长为2的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $P$ 在线段 $B D_{1}$ 上运动（包括端点），下列选项正确的有（）

A、 $A P ⊥ B_{1} C$ B、 $P D ⊥ B C$ C、直线 $P C_{1}$ 与平面 $A_{1} B C D_{1}$ 所成角的最小值是 $\frac{π}{6}$ D、 $P C + P D$ 的最小值为 $2 \sqrt{3}$

查看试题解析
11. 已知 $f (x) = x^{3} + b x^{2} + x + d$ ， $b ， d \in R$ ，下列说法正确的是（）

A、存在 $b ， d$ 使得 $f (x)$ 是奇函数 B、任意 $b$ ､ $d ， f (x)$ 的图象是中心对称图形 C、若 $x_{1} ， x_{2}$ 为 $f (x)$ 的两个极值点，则 $x_{1}^{2} + x_{2}^{2} > 1$ D、若 $f (x)$ 在 $R$ 上单调，则 $- \sqrt{3} \leq b \leq \sqrt{3}$

查看试题解析
12. 已知 $F_{1} 、 F_{2}$ 分别为双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左、右焦点，过点 $F_{2}$ 的直线与双曲线的右支交于 $A 、 B$ 两点，记 $△ A F_{1} F_{2}$ 的内切圆 $I_{1}$ 的半径为 $r_{1} ， △ B F_{1} F_{2}$ 的内切圆 $I_{2}$ 的半径为 $r_{2}$ ，若 $r_{1} r_{2} = a^{2}$ ，则（）

A、 $I_{1}$ 、 $I_{2}$ 在直线 $x = a$ 上 B、双曲线的离心率 $e = 2$ C、 $△ A B F_{1}$ 内切圆半径最小值是 $\frac{3}{2} a$ D、 $r_{1} + r_{2}$ 的取值范围是 $[2 a ， \frac{4 \sqrt{3}}{3} a]$

查看试题解析

三、填空题

13. $(y - 2) (x - 3)^{4}$ 的展开式中含 $x^{3} y$ 项的系数为.

查看试题解析
14. 已知正项等差数列 ${a_{n}}$ 满足 $3 a_{n} = a_{3 n}$ ，且 $a_{4}$ 是 $a_{3} - 3$ 与 $a_{8}$ 的等比中项，则 ${a_{n}}$ 的前 $n$ 项和 $S_{n} =$ .

查看试题解析
15. 过点 $P (4 ， 5)$ 作圆 $C ： (x - 1)^{2} + (y - 2)^{2} = 4$ 的两条切线，切点分别为 $A ， B$ ，则 $A B$ 的直线方程为.

查看试题解析
16. 若函数 $f (x) = \frac{e^{x}}{x^{3}} - a (\frac{3}{x} + l n x)$ 只有一个极值点，则 $a$ 的取值范围是.

查看试题解析

四、解答题

17. 已知在 $△ A B C$ 中，边 $a$ ， $b$ ， $c$ 所对的角分别为 $A$ ， $B$ ， $C$ ， $\frac{s i n (B - A)}{s i n A} + \frac{s i n A}{s i n C} = 1$ .

(1)、证明： $a$ ， $b$ ， $c$ 成等比数列；

(2)、求角 $B$ 的最大值.

查看试题解析
18. 已知正项数列 ${a_{n}}$ ，其前 $n$ 项和 $S_{n}$ 满足 $a_{n} (2 S_{n} - a_{n}) = n ， n \in N^{*}$ .

(1)、求 ${a_{n}}$ 的通项公式；

(2)、证明： $\frac{1}{S_{1}^{2}} + \frac{1}{S_{2}^{2}} + ⋯ + \frac{1}{S_{n}^{2}} < 2$ .

查看试题解析
19. 如图，在三棱柱 $A B C - D E F$ 中， $A D = 2 A B = 4 ， ∠ B A D = \frac{π}{3} ， P$ 为 $A D$ 的中点， $△ B C P$ 为等边三角形，直线 $A C$ 与平面 $A B E D$ 所成角大小为 $\frac{π}{4}$ .

(1)、求证： $P E ⊥$ 平面 $B C P$ ；

(2)、求平面 $E C P$ 与平面 $P C D$ 夹角的余弦值.

查看试题解析
20. 某学校为了迎接党的二十大召开，增进全体教职工对党史知识的了解，组织开展党史知识竞赛活动并以支部为单位参加比赛.现有两组党史题目放在甲､乙两个纸箱中，甲箱有5个选择题和3个填空题，乙箱中有4个选择题和3个填空题，比赛中要求每个支部在甲或乙两个纸箱中随机抽取两题作答.每个支部先抽取一题作答，答完后题目不放回纸箱中，再抽取第二题作答，两题答题结束后，再将这两个题目放回原纸箱中.

(1)、如果第一支部从乙箱中抽取了2个题目，求第2题抽到的是填空题的概率；

(2)、若第二支部从甲箱中抽取了2个题目，答题结束后错将题目放入了乙箱中，接着第三支部答题，第三支部抽取第一题时，从乙箱中抽取了题目.已知第三支部从乙箱中取出的这个题目是选择题，求第二支部从甲箱中取出的是2个选择题的概率.

查看试题解析
21. 已知点 $M (4 ， 4)$ 在抛物线 $Γ ： x^{2} = 2 p y$ 上，过动点 $P$ 作抛物线的两条切线，切点分别为 $A$ ､ $B$ ，且直线 $P A$ 与直线 $P B$ 的斜率之积为 $- 2$ .

(1)、证明：直线 $A B$ 过定点；

(2)、过 $A$ ､ $B$ 分别作抛物线准线的垂线，垂足分别为 $C$ ､ $D$ ，问：是否存在一点 $P$ 使得 $A$ ､ $C$ ､ $P$ ､ $D$ 四点共圆？若存在，求所有满足条件的 $P$ 点；若不存在，请说明理由.

查看试题解析
22. 已知函数 $f (x) = \frac{1}{2} x^{2} - a c o s x + b x l n x - b x ， a ， b \in R$ .

(1)、若 $b = 0$ 且函数 $f (x)$ 在 $(0 ， \frac{π}{2})$ 上是单调递增函数，求 $a$ 的取值范围；

(2)、设 $f (x)$ 的导函数为 $f^{^{'}} (x)$ ，若 $0 < a < 1 ， x_{1} 、 x_{2}$ 满足 $f^{'} (x_{1}) = f^{'} (x_{2})$ ，证明： $\sqrt{x_{1}} + \sqrt{x_{2}} > 2 \sqrt{\frac{- b}{1 + a}}$ .

查看试题解析