2022~2023学年中考数学一轮复习专题18相似综合(压轴)
试卷更新日期:2022-12-14 类型:一轮复习
一、三角形相关
-
1. 如图,四边形 中, , , 于点D.若 , ,则线段 的长为.
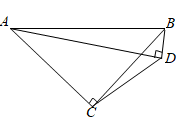 2. 如图,在Rt△ABC和Rt△BDE中,∠ABC=∠BDE=90°,点A在边DE的中点上,若AB=BC,DB=DE=2,连结CE,则CE的长为( )
2. 如图,在Rt△ABC和Rt△BDE中,∠ABC=∠BDE=90°,点A在边DE的中点上,若AB=BC,DB=DE=2,连结CE,则CE的长为( )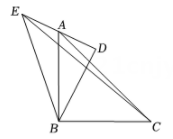 A、 B、 C、4 D、3. 如图, 中, , ,点D是边BC的中点,以AD为底边在其右侧作等腰三角形ADE,使 ,连结CE,则 的值为( )
A、 B、 C、4 D、3. 如图, 中, , ,点D是边BC的中点,以AD为底边在其右侧作等腰三角形ADE,使 ,连结CE,则 的值为( )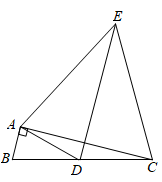 A、 B、 C、 D、24. 如图,在△ABC中,∠BAC=90°,AB=AC=12,点P在边AB上,D、E分别为BC、PC的中点,连接DE.过点E作BC的垂线,与BC、AC分别交于F、G两点.连接DG,交PC于点H.
A、 B、 C、 D、24. 如图,在△ABC中,∠BAC=90°,AB=AC=12,点P在边AB上,D、E分别为BC、PC的中点,连接DE.过点E作BC的垂线,与BC、AC分别交于F、G两点.连接DG,交PC于点H.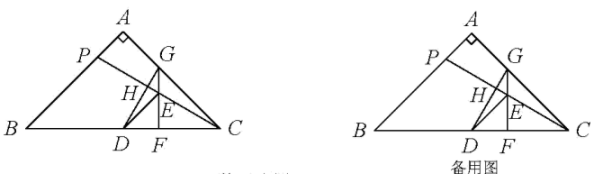 (1)、∠EDC的度数为;(2)、连接PG,求△APG 的面积的最大值;(3)、PE与DG存在怎样的位置关系与数量关系?请说明理由;(4)、求的最大值.5. 如图,四边形ABCD中,∠ADC=90°,AC⊥BC,∠ABC=45°,AC与BD交于点E,若AB= , CD=2,则△ABE的面积为 .
(1)、∠EDC的度数为;(2)、连接PG,求△APG 的面积的最大值;(3)、PE与DG存在怎样的位置关系与数量关系?请说明理由;(4)、求的最大值.5. 如图,四边形ABCD中,∠ADC=90°,AC⊥BC,∠ABC=45°,AC与BD交于点E,若AB= , CD=2,则△ABE的面积为 .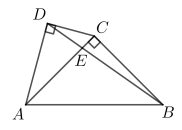 6. 已知:点C,D均在直线l的上方,与都是直线l的垂线段,且在的右侧, , 与相交于点O.
6. 已知:点C,D均在直线l的上方,与都是直线l的垂线段,且在的右侧, , 与相交于点O.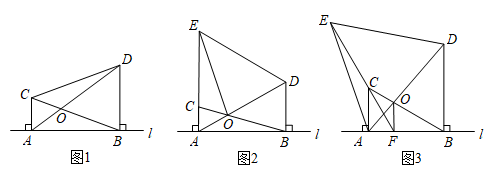 (1)、如图1,若连接 , 则的形状为 , 的值为;(2)、若将沿直线l平移,并以为一边在直线l的上方作等边.
(1)、如图1,若连接 , 则的形状为 , 的值为;(2)、若将沿直线l平移,并以为一边在直线l的上方作等边.①如图2,当与重合时,连接 , 若 , 求的长;
②如图3,当时,连接并延长交直线l于点F,连接.求证:.
7.(1)、【问题呈现】如图1,△ABC和△ADE都是等边三角形,连接BD,CE.求证:BD=CE.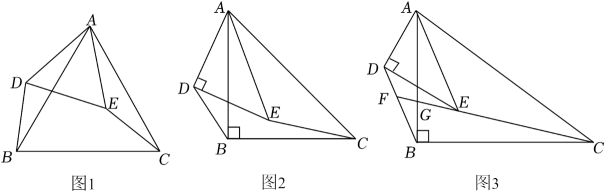 (2)、【类比探究】如图2,△ABC和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°.连接BD,CE.请直接写出的值.(3)、【拓展提升】如图3,△ABC和△ADE都是直角三角形,∠ABC=∠ADE=90°,且== . 连接BD,CE.
(2)、【类比探究】如图2,△ABC和△ADE都是等腰直角三角形,∠ABC=∠ADE=90°.连接BD,CE.请直接写出的值.(3)、【拓展提升】如图3,△ABC和△ADE都是直角三角形,∠ABC=∠ADE=90°,且== . 连接BD,CE.①求的值;
②延长CE交BD于点F,交AB于点G.求sin∠BFC的值.
8. 如图,等边 的边长为3,点D在边 上, ,线段 在边 上运动, ,有下列结论:
① 与 可能相等;② 与 可能相似;③四边形 面积的最大值为 ;④四边形 周长的最小值为 .其中,正确结论的序号为( )
A、①④ B、②④ C、①③ D、②③9. 如图,在正方形ABCD的对角线AC上取一点E . 使得 ,连接BE并延长BE到F , 使 ,BF与CD相交于点H , 若 ,有下列结论:① ;② ;③ ;④ .则其中正确的结论有( )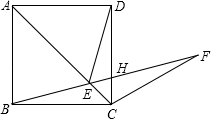 A、①②③ B、①②③④ C、①②④ D、①③④
A、①②③ B、①②③④ C、①②④ D、①③④二、矩形相关
-
10. 矩形ABCD中,=(k>1),点E是边BC的中点,连接AE,过点E作AE的垂线EF,与矩形的外角平分线CF交于点F.
 (1)、【特例证明】如图(1),当k=2时,求证:AE=EF;
(1)、【特例证明】如图(1),当k=2时,求证:AE=EF;小明不完整的证明过程如下,请你帮他补充完整.
证明:如图,在BA上截取BH=BE,连接EH.
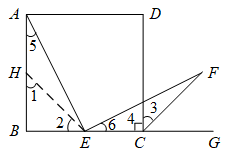
∵k=2,
∴AB=BC.
∵∠B=90°,BH=BE,
∴∠1=∠2=45°,
∴∠AHE=180°-∠1=135°.
∵CF平分∠DCG,∠DCG=90°,
∴∠3=∠DCG=45°.
∴∠ECF=∠3+∠4=135°.
∴……
(只需在答题卡对应区域写出剩余证明过程)
(2)、【类比探究】如图(2),当k≠2时,求的值(用含k的式子表示);(3)、【拓展运用】如图(3),当k=3时,P为边CD上一点,连接AP,PF,∠PAE=45°, , 求BC的长.11. 如图,矩形中, , 点E在折线上运动,将绕点A顺时针旋转得到 , 旋转角等于 , 连接 . (1)、当点E在上时,作 , 垂足为M,求证;(2)、当时,求的长;(3)、连接 , 点E从点B运动到点D的过程中,试探究的最小值.12. 如图1,在矩形ABCD中, , .点E是线段AD上的动点(点E不与点A,D重合),连接CE,过点E作 ,交AB于点F.
(1)、当点E在上时,作 , 垂足为M,求证;(2)、当时,求的长;(3)、连接 , 点E从点B运动到点D的过程中,试探究的最小值.12. 如图1,在矩形ABCD中, , .点E是线段AD上的动点(点E不与点A,D重合),连接CE,过点E作 ,交AB于点F. (1)、求证: ;(2)、如图2,连接CF,过点B作 ,垂足为G,连接AG.点M是线段BC的中点,连接GM.
(1)、求证: ;(2)、如图2,连接CF,过点B作 ,垂足为G,连接AG.点M是线段BC的中点,连接GM.①求 的最小值;
②当 取最小值时,求线段DE的长.
13. 如图,在矩形ABCD中,AB=6,BC=4,点M、N分别在AB、AD上,且MN⊥MC,点E为CD的中点,连接BE交MC于点F. (1)、当F为BE的中点时,求证:AM=CE;(2)、若=2,求的值;(3)、若MN∥BE,求的值.14. 如图,在矩形 中, , ,对角线 相交于点O,点P为边 上一动点,连接 ,以 为折痕,将 折叠,点A的对应点为点E,线段 与 相交于点F.若 为直角三角形,则 的长.
(1)、当F为BE的中点时,求证:AM=CE;(2)、若=2,求的值;(3)、若MN∥BE,求的值.14. 如图,在矩形 中, , ,对角线 相交于点O,点P为边 上一动点,连接 ,以 为折痕,将 折叠,点A的对应点为点E,线段 与 相交于点F.若 为直角三角形,则 的长. 15. 如图,在矩形 中, 分别为边 , 的中点, 与 , 分别交于点M , N . 已知 , ,则 的长为 .
15. 如图,在矩形 中, 分别为边 , 的中点, 与 , 分别交于点M , N . 已知 , ,则 的长为 .
三、四边形相关
-
16. 如图,已知菱形的边长为2,对角线相交于点O,点M,N分别是边上的动点, , 连接.以下四个结论正确的是( )

①是等边三角形;②的最小值是;③当最小时;④当时,.
A、①②③ B、①②④ C、①③④ D、①②③④17. 如图,在菱形ABCD中,AB=5,BD为对角线.点E是边AB延长线上的任意一点,连结DE交BC于点F,BG平分∠CBE交DE于点G. (1)、求证:.(2)、若 .
(1)、求证:.(2)、若 .①求菱形的面积.
②求的值.
(3)、若 , 当的大小发生变化时(),在AE上找一点T,使GT为定值,说明理由并求出ET的值.18. 如图,在边长为1的菱形中, , 动点E在边上(与点A、B均不重合),点F在对角线上,与相交于点G,连接 , 若 , 则下列结论错误的是( ) A、 B、 C、 D、的最小值为
A、 B、 C、 D、的最小值为四、正方形相关
-
19. 如图,在矩形 中,点E在边 上, 与 关于直线 对称,点B的对称点F在边 上,G为 中点,连结 分别与 交于M,N两点,若 , ,则 的长为 , 的值为.
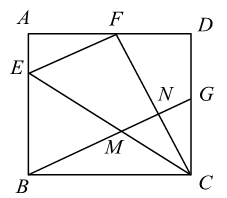 20. 如图,正方形ABCD的对角线AC,BD相交于点O,点F是CD上一点,交BC于点E,连接AE,BF交于点P,连接OP.则下列结论:①;②;③;④若 , 则;⑤四边形OECF的面积是正方形ABCD面积的 . 其中正确的结论是( )
20. 如图,正方形ABCD的对角线AC,BD相交于点O,点F是CD上一点,交BC于点E,连接AE,BF交于点P,连接OP.则下列结论:①;②;③;④若 , 则;⑤四边形OECF的面积是正方形ABCD面积的 . 其中正确的结论是( ) A、①②④⑤ B、①②③⑤ C、①②③④ D、①③④⑤21.(1)、【探究发现】如图①所示,在正方形中,为边上一点,将沿翻折到处,延长交边于点.求证:
A、①②④⑤ B、①②③⑤ C、①②③④ D、①③④⑤21.(1)、【探究发现】如图①所示,在正方形中,为边上一点,将沿翻折到处,延长交边于点.求证: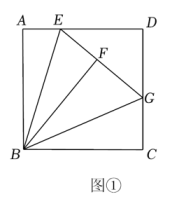 (2)、【类比迁移】如图②,在矩形中,为边上一点,且将沿翻折到处,延长交边于点延长交边于点且求的长.
(2)、【类比迁移】如图②,在矩形中,为边上一点,且将沿翻折到处,延长交边于点延长交边于点且求的长. (3)、【拓展应用】如图③,在菱形中,为边上的三等分点,AB=6,将沿翻折得到 , 直线交于点求的长.
(3)、【拓展应用】如图③,在菱形中,为边上的三等分点,AB=6,将沿翻折得到 , 直线交于点求的长.
五、折叠相关
-
22. 如图,把某矩形纸片 沿 , 折叠(点E、H在 边上,点F,G在 边上),使点B和点C落在 边上同一点P处,A点的对称点为 、D点的对称点为 ,若 , 为8, 的面积为2,则矩形 的长为( )
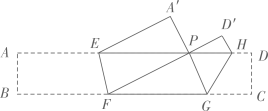 A、 B、 C、 D、23. 如图,将矩形 沿着 、 、 翻折,使得点 、 、 恰好都落在点 处,且点 、 、 在同一条直线上,同时点 、 、 在另一条直线上.小炜同学得出以下结论:
A、 B、 C、 D、23. 如图,将矩形 沿着 、 、 翻折,使得点 、 、 恰好都落在点 处,且点 、 、 在同一条直线上,同时点 、 、 在另一条直线上.小炜同学得出以下结论:① ;② ;③ ;④ ;⑤ .
其中正确的是( )
 A、①②③ B、①③④ C、①④⑤ D、②③④
A、①②③ B、①③④ C、①④⑤ D、②③④