（苏科版）2022-2023学年九年级数学下册8.2 货比三家 同步测试
试卷更新日期：2022-12-14 类型：同步测试
一、单选题
-
1. 在线教育使学生足不出户也能连接全球优秀的教育资源. 下面的统计图反映了我国在线教育用户规模的变化情况.
（以上数据摘自《2017年中国在线少儿英语教育白皮书》）
根据统计图提供的信息，下列推断一定不合理的是（ ）
A、2015年12月至2017年6月，我国在线教育用户规模逐渐上升 B、2015年12月至2017年6月，我国手机在线教育课程用户规模占在线教育用户规模的比例持续上升 C、2015年12月至2017年6月，我国手机在线教育课程用户规模的平均值超过7000万 D、2017年6月，我国手机在线教育课程用户规模超过在线教育用户规模的70%2. 下列六个数：0、 中，无理数出现的频数是（ ）A、3 B、4 C、5 D、63. 在一次训练中，甲、乙、丙三人各射击10次的成绩如图所示（单位：环），在这三人中，此次射击成绩最稳定的是
A、甲 B、乙 C、丙 D、无法判断4. 某班有 位学生，每人抛 次硬币，统计正面向上次数依次为 ， ， ，…， 的人数，得到直方图（如图），记正面向上次数为 ， ， 的人数和占班级人数的比例为 ，则 的值（ ）
A、小于
B、在 与 
之间
C、在 与 
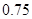之间
D、大于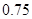
5. 某校测量了初三 班学生的身高（精确到 ），按 为一段进行分组，得到如下频数分布直方图，则下列说法正确的是（ ）
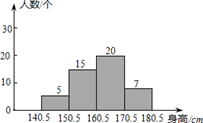A、该班人数最多的身高段的学生数为
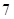人
B、该班身高低于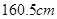 
的学生数为 
人
C、该班身高最高段的学生数为 
人
D、该班身高最高段的学生数为 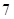人
6. 某人在调查了本班同学的体重情况后，画出了频数分布图如图．下列结论中，不正确的是（ ）
A、全班总人数40人 B、学生体重的众数是13 C、学生体重的中位数落在50～55千克这一组 D、体重在60～65千克的人数占全班总人数的
7. 某校组织400名九年级学生参加英语测试，为了解他们的测试情况（满分120分），随机抽取若干名学生，将所得成绩数据整理后，画出频数分布直方图（如图）．估计该校成绩在100～120分之间的人数有（ ）
A、12 B、48 C、60 D、728. 如图，表示某地区各年龄层人口的累积百分率，其资料自0岁开始，每10岁为一组．根据此图，判断下列关于此地居民的叙述，何者正确？（ ）
A、可能有100岁的老人 B、21～80岁之间的居民占五成以上的比例 C、30岁以上的人数比20岁以下的人数少 D、居民年龄在40～60岁之间的人口累积百分率是50%9. 如图是某班40名学生一分钟跳绳测试成绩（次数为整数）的频数分布直方图，从左起第一、二、三、四个小长方形的高的比为1：4：3：2，那么该班一分钟跳绳次数在100次以上的学生有（ ）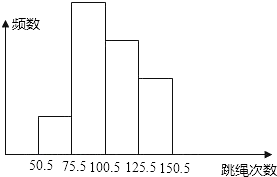
A、6人 B、8人 C、16人 D、20人10.为了了解本校九年级学生的体能情况，随机抽查了其中30名学生，测试了1分钟仰卧起坐的次数，并绘制成如图所示的频数分布直方图，请根据图示计算，仰卧起坐次数在25～30次的频率是（ ）
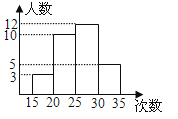A、0.1 B、0.2 C、0.3 D、0.4二、填空题
-
11. “无糖饮料”真的不含糖吗？某探究小组对市面上35款无糖饮料进行含糖量测评统计，得到35频数直方图（每一组含前一个边界值，不含后一个边界值）如图所示，根据《食品安全国家标准》，每100毫升饮料含糖量低于500毫克，即可标注“零糖”，则名副其实的饮料有款．
12. 如图是小明在抛掷图钉的试验中得到的图钉针尖朝上的折线统计图，请你估计抛掷图钉针尖朝上的概率是.
13. 如图是九（1）班45名同学每周课外阅读时间的频数分布直方图（每组含前一个边界值，不含后一个边界值）.其中每周课外阅读时间在6小时及以上的人有名.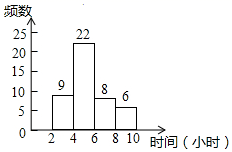
14. 随着黄石市精神文明建设的不但推进，市民每天用于读书、读报、参加“全民健身运动”的时间越来越多．如图是我市晚报记者在抽样调查了一些市民用于上述活动的时间后，绘制的频率分布直方图，从左到右的前七个长方形面积之和为 ，最后一组的频数是 ，则此次抽样的样本容量是 ．
15. 在列频数分布表时，得到某数据的频数是 ，频率是 ，那么这组数据共有个．三、解答题
-
16. 为了传承中华优秀传统文化，市教育局决定开展“经典诵读进校园”活动，某校团委组织八年级100名学生进行“经典诵读”选拔赛，赛后对全体参赛学生的成绩进行整理，得到下列不完整的统计图表。
组别
分数段
频次
频率
A
60⩽x<70
17
0.17
B
70⩽x<80
30
a
C
80⩽x<90
b
0.45
D
90⩽x<100
8
0.08
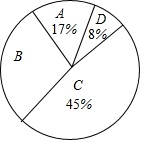
请根据所给信息，解答以下问题：
(1)、表中a= ， b=；(2)、请计算扇形统计图中B组对应扇形的圆心角的度数；(3)、已知有四名同学均取得98分的最好成绩，其中包括来自同一班级的甲、乙两名同学，学校将从这四名同学中随机选出两名参加市级比赛，请用列表法或画树状图法求甲、乙两名同学都被选中的概率。17.在射击竞赛的选拔赛中，运动员甲10次射击成绩的统计表和扇形统计图如下：
（1）根据统计表（图）中提供的信息，补全统计表及扇形统计图；
（2）已知乙运动员10次射击的平均成绩为9环，方差为1.2，如果只能选一人参加比赛，你认为应该派谁去？并说明理由.18.某校举办的课外活动中，有一项是小制作评比.作品上交时限为3月1日至30日，组委会把同学们交来的作品按时间顺序每5天组成一组，对每一组的件数进行统计，绘制成如图所示的统计图.已知从左到右各矩形的高度比为2：3：4：6：4：1. 第三组的件数是12. 请你回答：
(1)本次活动共有__________件作品参赛；各组作品件数的中位数是_________件.
(2)经评比，第四组和第六组分别有10件和2件作品获奖，那么你认为这两组中哪个组获奖率较高？为什么？
(3)小制作评比结束后，组委会决定从4件最优秀的作品A、B、C、D中选出两件进行全校展示，请用树状图或列表法求出刚好展示B、D的概率.四、综合题
-
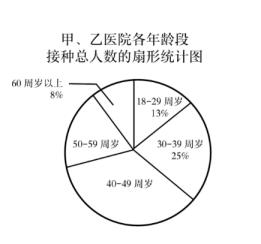
19. 自疫情暴发以来，我国科研团队经过不懈努力，成功地研发出了多种新冠疫苗，以下是某地甲、乙两家医院5月份某天各年龄段接种疫苗人数的频数分布表和接种总人数的形统计图：
甲医院
乙医院
年龄段
频数
频率
频数
频率
18—29周岁
900
0.15
400
0.1
30—39周岁
a
0.25
1000
0.25
40—49周岁
2100
b
c
0.225
50—59周岁
1200
0.2
1200
0.3
60周岁以上
300
0.05
500
0.125
(1)、根据上面图表信息，回答下列问题：①填空：a= ， b= ， c=；
②在甲、乙两医院当天接种疫苗的所有人员中，40—49周岁年龄段人数在扇形统计图中所占圆心角为；
(2)、若A，B，C三人都于当天随机到这两家医院接种疫苗，请用列表或画树状图的方法求这三人在同一家医院接种的概率．20. 甲、乙两校各组织300名学生参加联赛，为了解两校联赛成绩情况，在两校随机抽取部分学生的联赛成绩，两校抽取的人数相等，结果如下（数据包括左端点不包括右端点）．甲校抽取的学生联赛成绩频数分布表
分组
频数
30≤x<40
1
40≤x<50
2
50≤x<60
5
60≤x<70
9
70≤x<80
11
80≤x<90
15
90≤x<10
7
(1)、若小明是乙校的学生，他的成绩是75分，请结合数据分析小明的成绩；(2)、若甲校中一位同学的成绩不纳入计算后，甲校的平均成绩提高了，这位同学的成绩不可能在哪些分数段？(3)、请用适当的统计量从两个不同角度分析哪所学校的联赛成绩整体较好？21. 国务院办公厅2015年3月16日发布了《中国足球改革的总体方案》，这是中国足球历史上的重大改革．为了进一步普及足球知识，传播足球文化，我市举行了“足球进校园”知识竞赛活动，为了解足球知识的普及情况，随机抽取了部分获奖情况进行整理，得到下列不完整的统计图表：获奖等次
频数
频率
一等奖
10
0.05
二等奖
20
0.10
三等奖
30
b
优胜奖
a
0.30
鼓励奖
80
0.40
请根据所给信息，解答下列问题：
(1)、a= ▲ ， b= ▲ ， 且补全频数分布直方图；(2)、若用扇形统计图来描述获奖分布情况，问获得优胜奖对应的扇形圆心角的度数是多少？(3)、在这次竞赛中，甲、乙、丙、丁四位同学都获得一等奖，若从这四位同学中随机选取两位同学代表我市参加上一级竞赛，请用树状图或列表的方法，计算恰好选中甲、乙二人的概率．22. “温故而知新，可以为师矣”古人把经常复习当作是一种乐趣，某班主任为了了解该班学生每周的复习情况，对该班学生每周的复习时间进行了调查，复习时间四舍五入后只有4种：1小时，2小时，3小时，4小时，已知该班共有50人，其中女生有20人.根据调查结果，制作了两幅不完整的统计图表：
女生一周复习时间频数分布表
复习时间
频数（学生人数）
1小时
3
2小时
a
3小时
5
4小时
7
该班男生和女生一周复习时间的平均数、中位数、众数如下：
性别
平均数
中位数
众数
男生
b
2
2
女生
2.65
c
2
根据以上信息，解答下列问题：
(1)、填空：a= ， b= ， c=.(2)、根据以上数据，你认为该班男生复习情况好还是女生复习情况好？请写出一条理由.(3)、该校九年级共有800名学生，通过计算估计一周复习时间为4小时的学生有多少名？23. 为了了解我市中学生参加“科普知识”竞赛成绩的情况，随机抽查了部分参赛学生的成绩，整理并制作出如下的统计表和统计图，如图所示.请根据图表信息解答下列问题：组别
分数段（分）
频数
频率
A组
60≤x＜70
30
0.1
B组
70≤x＜80
90
n
C组
80≤x＜90
m
0.4
D组
90≤x＜100
60
0.2
(1)、在表中：m＝ ， n＝；(2)、补全频数分布直方图；(3)、小明的成绩是所有被抽查学生成绩的中位数，据此推断他的成绩在组；(4)、4个小组每组推荐1人，然后从4人中随机抽取2人参加颁奖典礼，恰好抽中A、C两组学生的概率是多少？并列表或画树状图说明.